رياضيات فصل أول

أتحقق من فهمي (صفحة 68) :

أجد مشتقة الاقتران $f\left(x\right)=4x^2+1$ باستعمال التعريف العام للمشتقة عندما $x=-1$.

الحل:

$$\begin{gathered} f^{\text{'}}\left(x\right)=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ {f}^{\text{'}}(-1)=\underset{h\to 0}{lim}\frac{f(-1+h)-f(-1)}{h}=\underset{h\to 0}{lim}\frac{4{(h-1)}^2+1-\left(5\right)}{h} \\ =\underset{h\to 0}{lim}\frac{4h^2-8h+4-4}{h}=\underset{h\to 0}{lim}\frac{h(4h-8)}{h}=-8 \end{gathered}$$

---

أتحقق من فهمي (صفحة 68) :

أجد مشتقة الاقتران $y=8-x^2$ باستعمال التعريف العام للمشتقة:

الحل:

$$\begin{gathered} \frac{dy}{dx}=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ =\underset{h\to 0}{lim}\frac{8-{(x+h)}^2-8+x^2}{h} \\ =\underset{h\to 0}{lim}\frac{8-x^2-2xh-h^2-8+x^2}{h} \\ =\underset{h\to 0}{lim}\frac{-2xh-h^2}{h}=\underset{h\to 0}{lim}\frac{h(-2x-h)}{h}=\underset{h\to 0}{lim}(-2x-h)=-2x \\ \Rightarrow \frac{dy}{dx}=-2x \end{gathered}$$

---

أتحقق من فهمي (صفحة 69) :

جد مشتقة كل اقتران مما يأتي : 

1) $y=x^{-11}$                2) $y=\frac{1}{x^5}$                   3) $y=\sqrt[3]{x^5 }$

الإجابة:

1) $\frac{dy}{dx}=-11x^{-12}=\frac{-11}{x^{12}}$ 

2) $\frac{dy}{dx}=-5x^{-6}=\frac{-5}{x^6}$

3) $y=\sqrt[3]{x^5 } \Rightarrow y=x^{\frac{5}{3}}$

$\frac{dy}{dx}=\frac{5}{3}{x}^{\frac{2}{3}}=\frac{5}{3\sqrt[3]{x^2}}$

---

أتحقق من فهمي صفحة (70):

أجد مشتقة كل اقتران مما يأتي :

1) $y=\sqrt{x}+\frac{4}{x^2}$           2) $y=\frac{x^5-8x^6}{4x}$

الإجابة:

1) $y=x^{\frac{1}{2}}+4x^{-2}$

$\frac{dy}{dx}=\frac{1}{2}{x}^{\frac{-1}{2}}-8x^{-3}=\frac{1}{2\sqrt{x}}-\frac{8}{x^3}$

2) $y=\frac{1}{4}{x}^4-2x^5$

$\frac{dy}{dx}=x^3-10x^4$

---

أتحقق من فهمي صفحة (72):

اذا كان الاقتران $y=8x-\frac{1}{x}$ ، فأستعمل المشتقة لإيجاد معادلة المماس ومعادلة العمودي على المماس عن النقطة $(0.25,-2)$.

الإجابة:

$y=8x-\frac{1}{x} , (0.25,-2)$

$\frac{dy}{dx}=8+\frac{1}{x^2}$

$m=\frac{dy}{dx}{|}_{x=0.25}=8+\frac{1}{(0.25{)}^2}=24$

$y-y_1=m(x-x_1)$

$y+2=24(x-0.25)$

$y+2=24x-6$

$y=24x-8 \mathrm{المماس} \mathrm{معادلة}$

- ميل العمودي على المماس: $\frac{-1}{24}$

$y-y_1=\frac{-1}{m}(x-x_1)$

$y+2=\frac{-1}{24}(x-0.24)$

$y+2=\frac{-1}{24}x+\frac{1}{96}\Rightarrow y=\frac{-1}{24}x-\frac{91}{96}$

---

أتحقق من فهمي صفحة (74):

a) جد أحداثيي النقطة الواقعة على منحنى الاقتران: $f\left(x\right)=1-\sqrt{x}$ ، التي يكون عندها ميل المماس $\frac{-1}{4}$

b) جد إحداثيي النقطة (النقاط) الواقعة على منحنى الاقتران: $f\left(x\right)=-x^3+3x^2-2$ التي يكون عندها المماس أفقياً .

الإجابة:

a) $f\left(x\right)=1-\sqrt{x}$

- نجد الاحداثي  xلنقطة التماس .

$f\left(x\right)=1-x^{\frac{1}{2}}$

$$\begin{gathered} f\text{'}\left(x\right)=-\frac{1}{2}{x}^{-\frac{1}{2}} \\ -\frac{1}{2\sqrt{x}}=-\frac{1}{4} \\ -4=-2\sqrt{x} \\ 2\sqrt{x}=4 \to x=4 \end{gathered}$$

- نجد الاحداثي y لنقطة التماس .$f\left(4\right)=1-\sqrt{4}=-1$

- اذن احداثي نقطة التماس هو: $(4,-1)$

 

b) $$\begin{gathered} f^{\text{'}}\left(x\right)=-2x^2+6x=0 \\ -2x(x-3)=0 \\ x=0,x=3 \end{gathered}$$

$$\begin{gathered} f\left(0\right)=-2 \\ f\left(3\right)=-27+27-2=-2 \end{gathered}$$

- اذن احداثي نقطة التماس  التي يكون عندهما المماس افقياً هو: $(0,-2)،(3,-2)$

---

---

أتدرب وأحل المسائل صفحة (74):

أجد مشتقّة كلٍّ من الاقترانات الآتية عند قيمة x المعطاة إزاء كلٍّ منها باستعمال التعريف العام للمشتقّة:

1) $f\left(x\right)=4x^2,x=1$                 2) $f\left(x\right)=1-x^2,x=-2$         3) $f\left(x\right)=x^2+x,x=2$               4) $f\left(x\right)=x^2-2x+3,x=-1$

الحل:

$$\begin{gathered} \mathbf{1}\mathbf{)}\mathbf{ }{f}^{\text{'}}(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ {f}^{\text{'}}(1)=\underset{h\to 0}{lim}\frac{f(1+h)-f\left(1\right)}{h}=\underset{h\to 0}{lim}\frac{4{(1+h)}^2+-{\left(4\right)}^2}{h} \\ =\underset{h\to 0}{lim}\frac{4+8h+h^2-4}{h}=\underset{h\to 0}{lim}\frac{h(8+h)}{h}=8 \end{gathered}$$

$$\begin{gathered} \mathbf{2}\mathbf{)} f^{\text{'}}(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ {f}^{\text{'}}(-2)=\underset{h\to 0}{lim}\frac{f(-2+h)-f(-2)}{h}=\underset{h\to 0}{lim}\frac{1-4{(-2+h)}^2+3}{h} \\ =\underset{h\to 0}{lim}\frac{1-(4-8h+h^2)+3}{h}=\underset{h\to 0}{lim}\frac{1-4+8h-h^2+3}{h}=\underset{h\to 0}{lim}(4-h)=4 \end{gathered}$$

$$\begin{gathered} \mathbf{3}\mathbf{)} f^{\text{'}}(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ {f}^{\text{'}}(2)=\underset{h\to 0}{lim}\frac{f(2+h)-f\left(2\right)}{h}=\underset{h\to 0}{lim}\frac{{(2+h)}^2+(2+h)-6}{h} \\ =\underset{h\to 0}{lim}\frac{4+4h+h^2+2+h-6}{h}=\underset{h\to 0}{lim}\frac{5h+h^2}{h}=\underset{h\to 0}{lim}(5+h)=5 \end{gathered}$$

$$\begin{gathered} \mathbf{4}\mathbf{)} f^{\text{'}}(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ {f}^{\text{'}}(-1)=\underset{h\to 0}{lim}\frac{f(-1+h)-f(-1)}{h}=\underset{h\to 0}{lim}\frac{{(-1+h)}^2-2(-1+h)+3-6}{h} \\ =\underset{h\to 0}{lim}\frac{1-2h+h^2+2-2h-3}{h}=\underset{h\to 0}{lim}\frac{-4h+h^2}{h}=\underset{h\to 0}{lim}(-4+h)=-4 \end{gathered}$$

---

أجد مشتقّة كلٍّ من الاقترانات الآتية باستعمال التعريف العامّ للمشتقّة:

5) $f\left(x\right)=4x+1$          6) $y=1-x$         7) $f\left(x\right)=\frac{1}{2}{x}^2-1$             8) $y=\frac{2x+4}{6}$

الحل:

$$\begin{gathered} \mathbf{6}\mathbf{)} \frac{dy}{dx}=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ =\underset{h\to 0}{lim}\frac{1-(x+h)-1+x}{h} \\ =\underset{h\to 0}{lim}\frac{1-x-h-1+x}{h}=\underset{h\to 0}{lim}(\frac{-h}{h})=-1 \end{gathered}$$

$$\begin{gathered} \mathbf{7}\mathbf{)} f\text{'}(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ =\underset{h\to 0}{lim}\frac{{\displaystyle f{(x+h)}^2-f\left(x\right)}}{h} \\ =\underset{h\to 0}{lim}\frac{{\displaystyle \frac{1}{2}}{(x+h)}^2-1-{\displaystyle \frac{1}{2}}{x}^2+1}{h} \\ =\underset{h\to 0}{lim}\frac{{\displaystyle \frac{1}{2}{x}^2+xh+\frac{1}{2}{h}^2-\frac{1}{2}{x}^2}}{h}=\underset{h\to 0}{lim}(\frac{{\displaystyle h(x+\frac{1}{2}h)}}{h})=x \end{gathered}$$

$$\begin{gathered} \mathbf{8}\mathbf{)} \frac{dy}{dx}=\underset{h\to 0}{lim}\frac{f(x+h)-f\left(x\right)}{h} \\ =\underset{h\to 0}{lim}\frac{{\displaystyle \frac{2x+2h+4}{6}}-\frac{2x+4}{6}}{h} \\ =\underset{h\to 0}{lim}\frac{\frac{2x+2h+4-2x-4}{6}}{h}=\underset{h\to 0}{lim}(\frac{{\displaystyle \frac{2h}{6}}}{h})=\frac{2h}{6h}=\frac{1}{3} \end{gathered}$$

---

أجد مشتقّة كلّ اقتران ممّا يأتي:

9) $y=10x-\frac{6}{\sqrt{x}}$           10) $y=x^8-x^{-8}$                         11) $y=9x^{-2}+3\sqrt{x}$

12) $y=\frac{1+\sqrt{x}}{x}$              13) $y=\frac{6}{x^3}+\frac{2}{x^2}-3$                 14) $y=20x^5+3\sqrt[3]{x}+17$

الحل:

$$\begin{gathered} \mathbf{12}\mathbf{)} y=\frac{1}{x}+\frac{\sqrt{x}}{x}=x^{-1}+x^{-\frac{1}{2}} \\ \frac{dy}{dx}=\frac{-1}{x^2}-\frac{1}{2\sqrt[3]{x}} \end{gathered}$$	$$\begin{gathered} \mathbf{9}\mathbf{)} y=10x-\frac{6}{\sqrt{x}}=10x-6x^{-\frac{1}{2}} \\ \frac{ dy}{dx}=10+3x^{-\frac{3}{2}}=10+\frac{3}{\sqrt{x^3}} \end{gathered}$$
$$\begin{gathered} \mathbf{13}\mathbf{)}\mathbf{ }y=\frac{6}{x^3}+\frac{2}{x^2}-3=6x^{-3}+2x^{-2}-3 \\ \frac{dy}{dx}=-18x^{-4}-4x^{-3}=\frac{-18}{x^4}-\frac{4}{x^3} \end{gathered}$$	$\mathbf{10}\mathbf{)}\mathbf{ }\frac{dy}{dx}=8x^7+8x^{-9}$
$$\begin{gathered} \mathbf{14}\mathbf{)} y=20x^5+3\sqrt[3]{x}+17 \\ \frac{dy}{dx}=100x^4+x^{-\frac{2}{3}}=100x^4+\frac{1}{\sqrt[3]{x^2}} \end{gathered}$$	$\mathbf{11}\mathbf{)} \frac{dy}{dx}=-18x^{-3}+\frac{3}{2}{x}^{-\frac{1}{2}}$

---

إذا كان الاقتران $y = x^2 - x$ ؛ فأستعمل المشتقّة لإيجاد كلّ ممّا يأتي:
15) معادلة المماس عندما x = 4
16) معادلة العمودي على المماس عندما x = 4

الحل:

$$\begin{gathered} \mathbf{16}\mathbf{)} m_{\mathrm{العمودي}}=\frac{-1}{7} \\ y-12=-\frac{1}{7}(x-4) \\ y=-\frac{1}{7}x+\frac{88}{7} \end{gathered}$$

$$\begin{gathered} \mathbf{15}\mathbf{)}\frac{ dy}{dx}{|}_{x=4}=2x-1 \\ m=2(4)-1=7 \\ y=16-4=12 \\ (4,12) \\ y-12=7(x-4) \\ y-12=7x-28 \\ y=7x-16 \end{gathered}$$

---

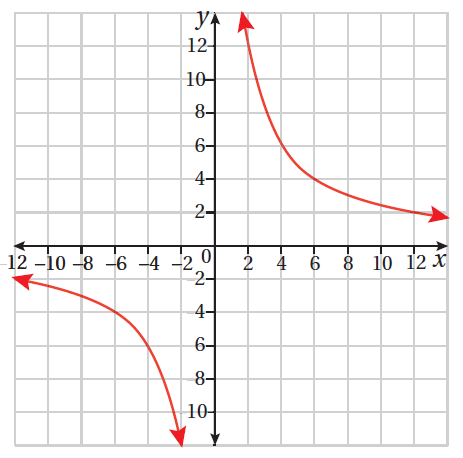يُمثّل الشكل المجاور منحنى الاقتران $f\left(x\right)=\frac{24}{x} , x \ne 0$ 17) أجد $f\text{'}\left(x\right)$ 18) أُبيّن أنّ ميل المماس سالب دائمًا عند أيّ نقطة. 19) أجد معادلة العمودي على المماس عندما $y=-6$

الحل:

17) $f^{\text{'}}\left(x\right)=\frac{-24}{x^2}$

18) اشارة $f^{\text{'}}\left(x\right)$  هي سالبة لكل قيم x ، حيث x≠0 اذاً ميل المماس دائماً سالب 

19) $y=\frac{24}{x} \to 6x=24 \to x=4$

 $$\begin{gathered} f^{\text{'}}\left(4\right)=\frac{-24}{(4{)}^2} \\ m=\frac{-24}{16}=\frac{-3}{2} \\ {m}_{\mathrm{العمودي}}=\frac{2}{3} \\ y-6=\frac{2}{3} (x-4) \\ y=\frac{2}{3}x-\frac{24}{3} \end{gathered}$$

---

20) أجد إحداثيي النقطة الواقعة على منحنى الاقتران: $f\left(x\right) = x^2 - x -12$ ، التي يكون عندها ميل المماس 3، ثم
أكتب معادلة هذا المماس.

الحل:

$$\begin{gathered} f^{\text{'}}\left(x\right)=2x-1 \\ m=f\text{'}\left(x\right)=3 \\ 2x-1=3 \\ x=2 \\ y=f\left(2\right)=4-2-12=-10 \\ (2,-10) \mathrm{النقطة} \end{gathered}$$

- اذن معادلة المماس : 

$$\begin{gathered} y+10=3(x-2) \\ y=3x-16 \end{gathered}$$

---

21) أجد إحداثيي النقطة (النقاط) الواقعة على منحنى الاقتران: $f\left(x\right)=x^3-4x^2-4$ ، التي يكون عندها المماس أفقيًّا.

الحل:

$$\begin{gathered} f^{\text{'}}\left(x\right)=3x^2-8x=0 \\ x(3x-8)=0 \\ x=0 , x=\frac{8}{3} \\ y=f\left(0\right)=0-0-4=-4 \\ y=f\left(\frac{8}{3}\right)=\frac{512}{27}-4\left(\frac{64}{9}\right)-4 \\ =\frac{512}{27}-\left(\frac{256}{9}\right)-4 \\ =\frac{512}{27}-\left(\frac{768}{27}\right)-\frac{108}{27}=-\frac{364}{27} \end{gathered}$$

$(0,-4)،(\frac{8}{3},(\frac{-364}{27}\left)\right) \mathrm{النقاط} \mathrm{احداثيات}$

22) أجد إحداثيي النقطة الواقعة على منحنى الاقتران: $f\left(x\right)=5x^2- 49x+12$ ، التي يكون عندها ميل المماس 1

الحل:

$m=f^{\text{'}}\left(x\right)=1$

$f^{\text{'}}\left(x\right)=10x-49=1$

$10x=50 \to x=5$

 

$$\begin{gathered} y=f\left(5\right)=5\left(100\right)-49\left(5\right)+12 \\ =500-245+12=267 \end{gathered}$$

احداثيات النقطة التي يكون عندها ميل المماس 1 هي : $(5,267)$

---

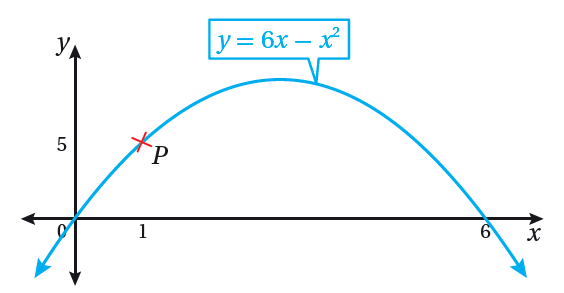يُبيّن الشكل المجاور منحنى الاقتران: $y=6x-x^2$ 23) أجد معادلة المماس لمنحنى الاقتران عند النقطة P 24) أجد معادلة العمودي على المماس لمنحنى الاقتران عند النقطة P

الحل:

23) $m=\frac{dy}{dx}{|}_{x=1}=6-2x=6-2\left(1\right)=4$

$$\begin{gathered} y-5=4(x-1) \\ y-5=4x-4 \\ y=4x+1 \end{gathered}$$

24) $m_{\mathrm{العمودي}}=\frac{-1}{4}$

$$\begin{gathered} y-5=\frac{-1}{4}(x-1) \\ y-5=\frac{-1 }{4}x+\frac{1}{4} \\ y=\frac{-1}{4} x+\frac{21}{4} \end{gathered}$$

---

مهارات التفكير العليا
تبرير: إذا كان: $f\left(x\right)=6-x^2$ ، فأجد كُلًًّّا ممّا يأتي:
25) معادلة المماس لمنحنى الاقتران ( f(x عند كلٍّ من النقطة $(5,1-)$ والنقطة $(5,1)$ ، أبرّر إجابتي.
26) نقطة تقاطع المماسين من الفرع السابق، أبرّر إجابتي.

الحل:

25) أولا: عند النقطة: $(-1,5)$

$$\begin{gathered} m=f^{\text{'}}\left(x\right)=-2x \\ m=-2(-1)=2 \\ y-5=2(x+1) \\ y-5=2x+2 \\ y=2x+7 \end{gathered}$$

ثانيا: عند النقطة: $(1,5)$

$$\begin{gathered} m=f^{\text{'}}\left(x\right)=-2x \\ m=-2\left(1\right)=-2 \\ y-5=-2(x-1) \\ y-5=-2x+2 \\ y=-2x+7 \end{gathered}$$

---

تبريرٌ: إذا كان الاقتران $y=x^2+4x$ ؛ فأُجيب عن السؤالين الآتيين تباعًا:
27) أُثبت أنّ معادلة المماس عند النقطة $x=k$ هي $y-(2k+4)x + k^2=0$

الحل:

$$\begin{gathered} m=f^{\text{'}}\left(x\right)=2x+4 \\ m=f^{\text{'}}\left(k\right)=2k+4 \\ y=f\left(k\right)=k^2+4k \\ y-(k^2+4k)=2k+4(x-k) \\ y-k^2-4k=2xk+4x-2k^2-4k \\ y-k^2-4k-2xk-4x+2k^2+4k=0 \\ y-(2k+4)x+k^2=0 \end{gathered}$$

---

28) أجد قيمة $k$ التي تكون عندها معادلة العمودي على المماس هي: $4y+ x=0$

الحل:

$4y=-x \to y=\frac{-1}{4}x$

ميل العمودي هو $\frac{-1}{4}$ وعندها يكون ميل المماس هو 4 

أي ان قيمة k التي تجعل المشتقة تساوي 4 

$\frac{dy}{dx}=2x \to 2k=4 \to k=2$

---

29) تحدّ: إذا كان: $f\left(x\right)=\frac{100}{x}$ ، وكانت $P$ نقطة تقع على منحنى $f\left(x\right)$ إحداثياها $(a,\frac{100}{a})$؛ ؛ فأجد مساحة المثلّث
المكوّن من مماس منحنى $f\left(x\right)$ عند النقطة P والمحورين الإحداثيّين.

الحل:

$f\left(x\right)=\frac{100}{x} , (a,100/a)$

$$\begin{gathered} f^{\text{'}}\left(x\right)=\frac{-100}{x^2} \\ {f}^{\text{'}}\left(a\right)=\frac{-100}{a^2} \\ y-\frac{100}{a}=\frac{-100}{a^2}(x-a) \end{gathered}$$

- المقطع x والمقطع y للمماس : 

$$\begin{gathered} x=0 \to y-\frac{100}{a}=\frac{-100}{a^2}(-a)=y=\frac{100}{a}+\frac{100}{a} \\ y=\frac{200}{a} \end{gathered}$$

$$\begin{gathered} y=0\to -\frac{100}{a}=-\frac{100}{a^2}(x-a) \\ -\frac{100}{a}=-\frac{100}{a^2}x+\frac{100}{a} \\ -\frac{100}{a^2}x=\frac{-200}{a} \\ x=\frac{\frac{200}{a}}{\frac{100}{a^2}}=\frac{200a^2}{100a}=2a \end{gathered}$$

$A=\frac{1}{2}\times 2a\times \frac{200}{a}=200$

---