رياضيات فصل أول

معادلة الدائرة هي العلاقة التي تربط بين الإحداثي x والإحداثي y  لكل نقطة واقعة على الدائرة. فإذا عرض احداثيا نقطة في المعادلة، وكانت النتيجة عبارة صحيحة، فهذا يعني أن تلك النقطة تقع على الدائرة 

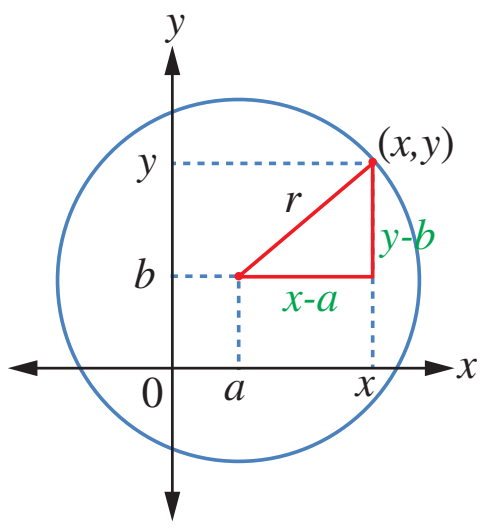
يمثل الشكل المجاور دائرة مركزها النقطة $\left(a,b\right)$، وطول نصف قطرها r. والنقطة $\left(x,y\right)$ تقع على الدائرة. ألاحظ أنه يمكن تكوين المثلث قائم الزاوية الذي طول ضلعه الأفقي $\left(x-a\right)$، وطول ضلعه الراسي $\left(y-b\right)$، وطول وتره r. وبتطبيق نظرية فيثاغورس تنتج المعادلة ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$ التي تسمى الطورة القياسية لمعادلة الدائرة 

مفهوم أساسي 

1) الصورة القياسية لمعادلة الدائرة التي مركزها النقطة $\left(a,b\right)$، وطول نصف قطرها r، هي: ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$

2) معادلة الدائرة التي مركزها نقطة الأصل $\left(0,0\right)$، وطول نصف قطرها r، هي: $x^2+y^2=r^2$

مثال 

اكتب معادلة الدائرة في كل من الحالات الآتية: 

1) المركز هو النقطة $\left(-2,7\right)$، وطول نصف القطر 6 وحدات 

$$\begin{gathered} {\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2 \\ {\left(x-\left(-2\right)\right)}^2+{\left(y-7\right)}^2=6^2 \\ {\left(x+2\right)}^2+{\left(y-7\right)}^2=36 \end{gathered}$$

2) المركز هو نقطة الأصل، وطول نصف القطر 5 وحدات 

$$\begin{gathered} x^2+y^2=r^2 \\ {x}^2+y^2=5^2 \\ {x}^2+y^2=25 \end{gathered}$$

3) الدائرة المرسومة في المستوى الإحداثي المجاور 

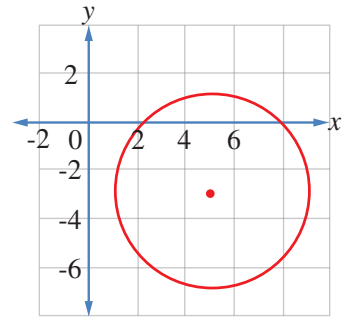
عند النظر إلى الدائرة يتبين أن مركزها النقطة $\left(5,-3\right)$، وأن طول نصف قطرها 4 وحدات 

$$\begin{gathered} {\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2 \\ {\left(x-5\right)}^2+{\left(y-\left(-3\right)\right)}^2=4^2 \\ {\left(x-5\right)}^2+{\left(y+3\right)}^2=16 \end{gathered}$$

إذا علم مركز الدائرة ونقطة واقعة عليها، فإنه يمكن إيجاد طول نصف القطر باستعمال قانون المسافة بين نقطتين، ثم كتابة معادلة الدائرة 

مراجعة المفهوم 

إذا كان طول القطعة المستقيمة الواصلة بين النقطتين $B\left(x_2,y_2\right)و،A\left(x_1,y_1\right)$، هو d فإن: $d^2={\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2$

مثال 

أجد معادلة الدائرة التي مركزها النقطة $\left(-7,13\right)$، وتمر بالنقطة $\left(5,4\right)$ 

أجد طول نصف القطر باستعمال قانون المسافة بين نقطتين: 

$$\begin{gathered} d^2={\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2 \\ {r}^2={\left(5-\left(-7\right)\right)}^2+{\left(4-13\right)}^2 \\ =144+81 \\ =225 \\ r=\sqrt{225}=15 \end{gathered}$$

ولأن، أعوض احداثيي المركز وقيمة $r^2$ في الصورة القياسية لمعادلة الدائرة، فأجد أن معادلة هذه الدائرة هي: 

${\left(x+7\right)}^2+{\left(y-13\right)}^2=225$

إذا علمنا معادلة دائرة بالصورة القياسية ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$، حيث $r>0$ فإنه يمكن فك الأقواس وإعادة الترتيب، فتنتج المعادلة: $x^2+y^2-2ax-2by+a^2+b^2-r^2=0$

يمكن أيضا كتابة هذه المعادلة بالصورة الآتية: 

$x^2+y^2+2fx+2gy+c=0$

حيث: $f=-a,g=-b,c=a^2+b^2-r^2$، وهي تسمى الصورة العامة لمعادلة الدائرة 

إذا علمنا الصورة العامة لمعادلة أي دائرة، فإنه يمكن تحويلها إلى الصورة القياسية ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$، وذلك بإكمال المربع 

مراجعة المفهوم 

لإكمال المربع للحدين $x^2+ax$، يضاف ${\left(\frac{a}{2}\right)}^2$، ثم يطرح،فينتج مربع كامل هو ${\left(x+\frac{a}{2}\right)}^2$ وبذلك يتحول $x^2+ax$ إلى ${\left(x+\frac{a}{2}\right)}^2-{\left(\frac{a}{2}\right)}^2$

مثال 

أجد إحداثيات المركز، وطول نصف القطر للدائرة $x^2+y^2-8x+6y-56=0$ 

بإكمال المربع للحدود التي تحوي x ينتج: $x^2-8x={\left(x-4\right)}^2-16$، وبإكمال المربع للحدود التي تحوي y ينتج: $y^2+6y={\left(y+3\right)}^2-9$

وبذلك يمكن تحويل المعادلة $x^2+y^2-8x+6y-56=0$ إلى: 

$$\begin{gathered} {\left(x-4\right)}^2-16+{\left(y+3\right)}^2-9-56=0 \\ {\left(x-4\right)}^2+{\left(y+3\right)}^2=81 \end{gathered}$$

بمقارنة هذه المعادلة بالصورة القياسية ${\left(x-a\right)}^2+{\left(y-b\right)}^2=r^2$، نجد أن: 

$a=4,b=-3,r=9$

إذن، مركز هذه الدائرة هو النقطة $\left(4,-3\right)$، وطول نصف قطرها 9 وحدات 

مثال 

أجد طول المماس المرسوم من النقطة $P\left(6,-6\right)$، الذي يمس الدائرة التي معادلتها 

${\left(x+5\right)}^2+{\left(y-4\right)}^2=25$

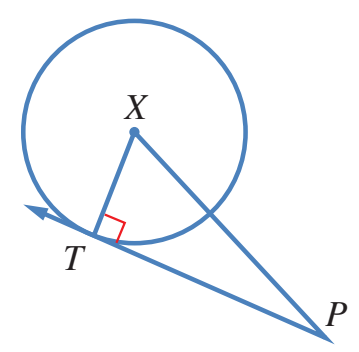
ارسم مخططا، ولتكن النقطة X مركز الدائرة، و T نقطة التماس 

لحساب طول المماس $\overline{PT}$، ثم أطبق نظرية فيثاغورس على المثلث القائم XTP، الذي يمكن إيجاد طولي ضلعين فيه، هما: نصف القطر $\overline{XT}$، والوتر $\overline{XP}$

طول نصف القطر XT هو 5. ولحساب XP، أجد المسافة بين مركز الدائرة $X\left(-5,4\right)$ والنقطة $P\left(6,-6\right)$ باستعمال قانون المسافة بين نقطتين: 

${\left(XP\right)}^2={\left(6-\left(-5\right)\right)}^2+{\left(-6-4\right)}^2={\left(11\right)}^2+{\left(-10\right)}^2=221$

وبتطبيق نظرية فيثاغورس على المثلث XTP:

$$\begin{gathered} {\left(PT\right)}^2={\left(XP\right)}^2-{\left(XT\right)}^2 \\ =221-25 \\ =196 \\ PT=\sqrt{196}=14 \end{gathered}$$

إذن، طول المماس 14 وحدة 

مثال 

اثبت ان المستقيم$y=2x+3$ هو مماس للدائرة التي معادلتها ${\left(x-10\right)}^2+{\left(y-8\right)}^2=45$ احل النظام المكون من المعادلتين: ${\left(x-10\right)}^2+{\left(y-8\right)}^2=45و، y=2x+3$؛ لايجاد عدد نقاط تقاطع المستقيم والدائرة. فاذا كان عدد نقاط التقاطع واحدا فقط، فان المستقيم يكون مماسا للدائرة

$$\begin{gathered} {\left(x-10\right)}^2+{\left(2x+3-8\right)}^2=45 \\ {\left(x-10\right)}^2+{\left(2x-5\right)}^2=45 \\ {x}^2-20x+100+4x^2-20x+25=45 \\ 5x^2-40x+80=0 \\ x^2-8x+16=0 \\ {\left(x-4\right)}^2=0 \\ x=4 \end{gathered}$$

                                                                  $y=2\left(4\right)+3=11$

بما ان هذا المستقيم يقطع الدائرة في نقطة واحدة هي $\left(4,11\right)$، فانه مماس للدائرة