رياضيات فصل ثاني

أتحقق من فهمي صفحة 125

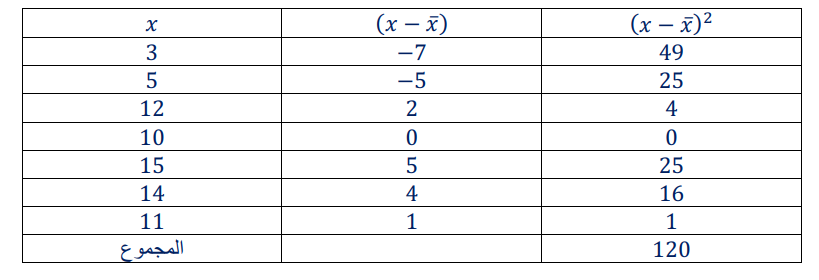
أجد التباين والانحراف المعياري لمجموعة البيانات الآتي: 

               3,5,12,10,15,14,11

$\overline{\mathbf{x}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{}\mathbf{x}}{\mathbf{n}}\mathbf{=}\mathbf{ }\frac{\mathbf{3}\mathbf{+}\mathbf{5}\mathbf{+}\mathbf{ }\mathbf{12}\mathbf{ }\mathbf{+}\mathbf{10}\mathbf{ }\mathbf{+}\mathbf{15}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{14}\mathbf{ }\mathbf{+}\mathbf{11}\mathbf{ }}{\mathbf{7}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{10}$

$$\begin{gathered} \mathbf{التبايبن}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{\sigma }}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{}{\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\overline{\mathbf{x}}\mathbf{ }\mathbf{)}}^{\mathbf{ }\mathbf{2}}}{\mathbf{n}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{120}}{\mathbf{7}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{17}\mathbf{.}\mathbf{14} \\ \mathbf{المعياري}\mathbf{ }\mathbf{الانحراف}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathit{\sigma }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{17}\mathbf{.}\mathbf{1}}\mathbf{ }\mathbf{=}\mathbf{4}\mathbf{.}\mathbf{14}\mathbf{ } \end{gathered}$$

---

أتحقق من فهمي صفحة 126

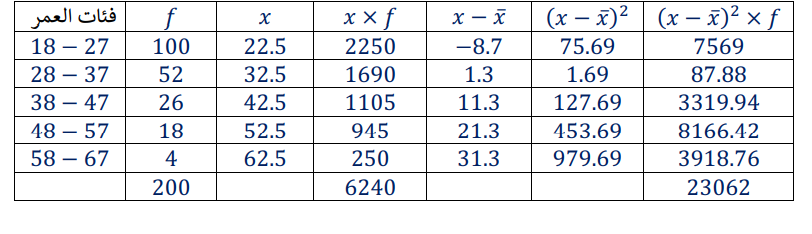
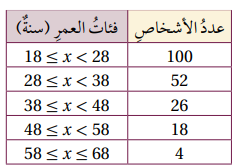
يبين الجدول المجاور توزيعا ل200 سائق وفق أعمارهم، ممن تسببوا في حوادث مرورية خطيرة في إحدى المدن على مدار  أسبوع. أقدر التباين والانحراف المعياري لهذه البيانات 

$$\begin{gathered} \overline{\mathbf{x}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{f}\mathbf{)}\mathbf{ }}{\mathbf{\sum }_{}\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{6240}}{\mathbf{200}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{31}\mathbf{.}\mathbf{2} \\ \mathbf{التبايبن}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{\sigma }}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\overline{\mathbf{x}}\mathbf{ }\mathbf{)}}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{f}}{\mathbf{\sum }_{\mathbf{ }}\mathbf{ }\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{23062}}{\mathbf{200}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{115}\mathbf{.}\mathbf{31} \\ \mathbf{المعياري}\mathbf{ }\mathbf{الانحراف}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathit{\sigma }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{115}\mathbf{.}\mathbf{31}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{10}\mathbf{.}\mathbf{74} \end{gathered}$$

---

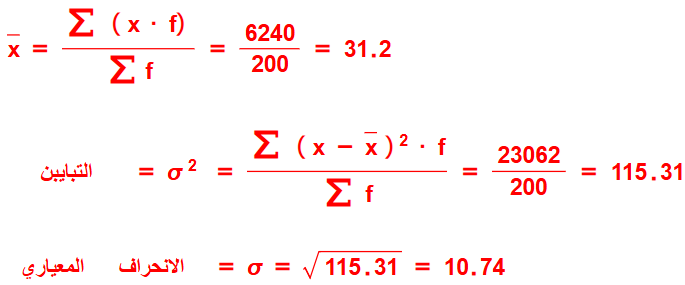
أتحقق من فهمي صفحة 127

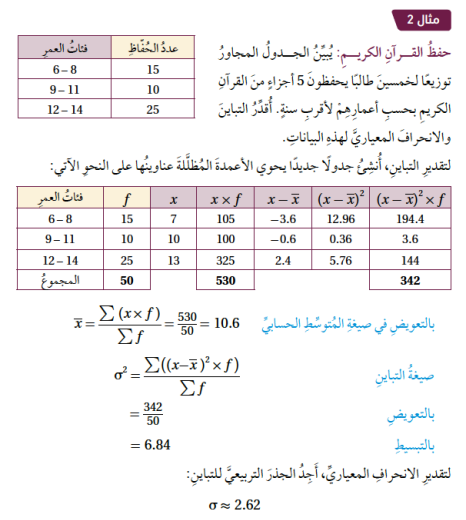
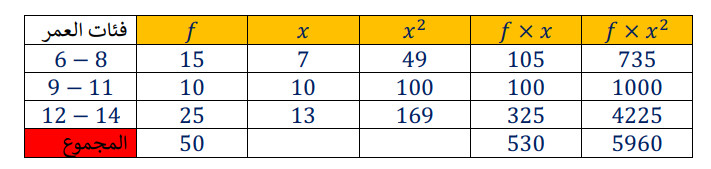
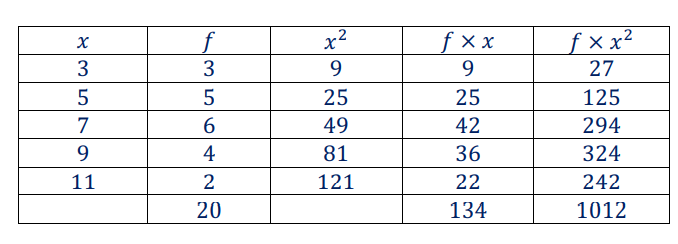
أحل مسألة (حفظ القرآن الكريم) التي وردت في المثال 2 باستعمال الصيغة الثانية لتقدير الانحراف المعياري التي أتوصل إليها بالقيمة التي سبق حسابها 

$$\begin{gathered} \overline{x } = \frac{\sum _{ }\left(x\times f\right)}{\sum f}=\frac{530}{50}=10.6 \\ \mathrm{التباين} = {\sigma }^2 =\frac{\sum \left(x^2 \times f\right) - \left(\sum f\right){\left(\overline{x}\right)}^2}{\sum f} ={\frac{5960-\left(50\right)\left(10.6\right)}{50}}^2 = 6.84 \\ \mathrm{المعياري} \mathrm{الانحراف} =\sigma = \sqrt{6.84 }\approx 2.62 \end{gathered}$$

 

---

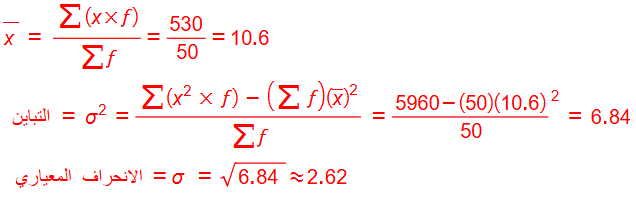
أتحقق من فهمي صفحة 128

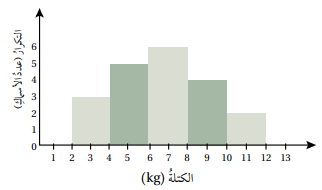
صيد بحري: يبين التمثيل بالمدرج التكراري المجاور  توزيعا لكتل مجموعة من الأسماك التي اصطادها أحد الصيادين في مدينة العقبة. أقد التباين والانحراف المعياري لهذه البيانات 

$$\begin{gathered} \overline{x } =\frac{\sum _{}x\times f}{\sum _{}f} = \frac{134}{20}= 6.7 \\ {\sigma }^2 =\frac{\sum _{}\left(x^2\times f\right)- \left(\sum _{}f\right){\left(\overline{x}\right)}^2}{\sum _{}f} =\frac{1012-\left(20\right){\left(6.7\right)}^2}{20}\approx 5.71 \end{gathered}$$

$\sigma =\sqrt{5.71} \approx 2.39$

 

---

أتدرب وأحل المسائل صفحة 129

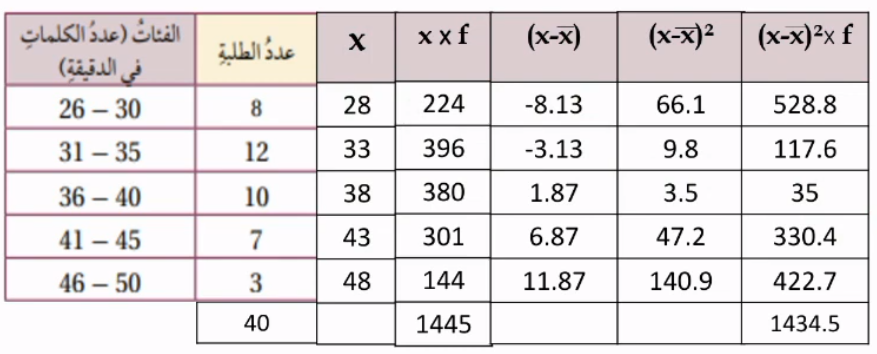
طباعة: يبين الجدول المجاور توزيعا لأربعين طالبا في الصف العاشر بحسب عدد الكلمات التي يستطيعون طباعتها في جهاز الحاسوب في دقيقة واحدة: 

 

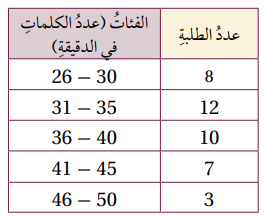
1) أقدر الوسط لهذه البيانات 

2)اقدر التباين و الانحراف المعياري لهذه البيانات

$$\begin{gathered} 1. \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\overline{\mathbf{x}}\mathbf{ }\mathbf{=}\frac{\mathbf{\sum }_{}\mathbf{(}\mathbf{x}\mathbf{\times }\mathbf{ }\mathbf{f}\mathbf{)}}{\mathbf{\sum }_{}\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{1445}}{\mathbf{40}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{36}\mathbf{.}\mathbf{125} \\ 2. \\ \mathbf{ }{\mathit{\sigma }}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{=}\frac{\mathbf{\sum }_{}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{-}\mathbf{ }{\overline{\mathbf{\left(}\mathbf{x}\mathbf{\right)}\mathbf{ }}\mathbf{)}}^{\mathbf{2}}\mathbf{ }\mathbf{\times }\mathbf{ }\mathbf{f}}{\mathbf{\sum }_{}\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{1434}\mathbf{.}\mathbf{5}}{\mathbf{40}}\mathbf{=}\mathbf{ }\mathbf{35}\mathbf{.}\mathbf{86} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{\sigma }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{5}\mathbf{.}\mathbf{99} \end{gathered}$$

 

---

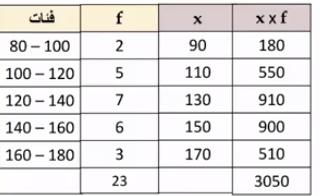
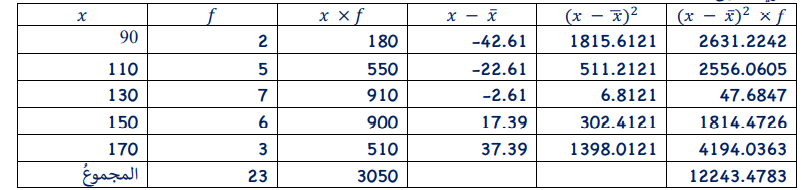
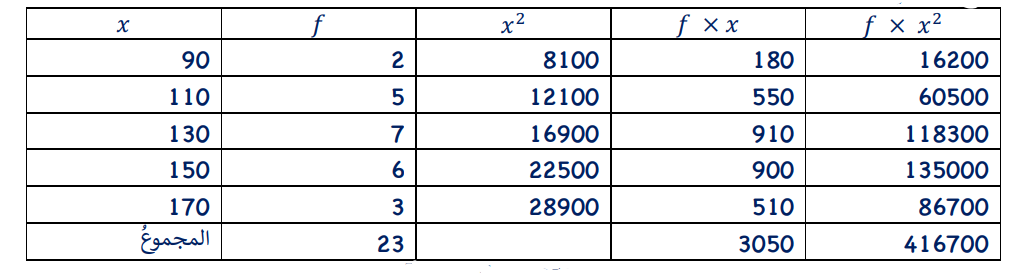
شقق سكنية: يبين الجدول المجاور توزيعا ل23 شقة سكنية-بحسب مساحاتها- بنتها إحدى شركات الإسكان عام 2020م:

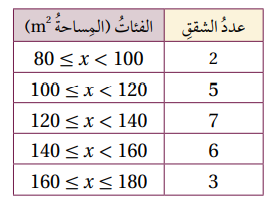
3) أقدر الوسط الحسابي لهذه البيانات 

4) أقدر التباين والانحراف المعياري لهذه البيانات بطريقتين مختلفتين 

 

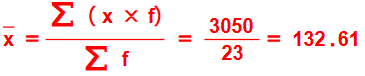$3. \mathbf{ }\mathbf{ }\overline{\mathbf{x}}\mathbf{ }\mathbf{=}\frac{\mathbf{\sum }_{}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{\times }\mathbf{ }\mathbf{f}\mathbf{)}}{\mathbf{\sum }_{}\mathbf{ }\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{3050}}{\mathbf{23}}\mathbf{=}\mathbf{ }\mathbf{132}\mathbf{.}\mathbf{61}$

4.

الطريقة الاولى

$$\begin{gathered} \overline{\mathbf{x}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{}\mathbf{x}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{f}}{\mathbf{\sum }_{}\mathbf{ }\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{3050}}{\mathbf{23}}\mathbf{\approx }\mathbf{ }\mathbf{132}\mathbf{.}\mathbf{61} \\ {\mathit{\sigma }}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{}{\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\overline{\mathbf{x}}\mathbf{ }\mathbf{)}}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{f}}{\mathbf{\sum }_{\mathbf{ }}\mathbf{f}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{12243}\mathbf{.}\mathbf{4783}}{\mathbf{23}}\mathbf{ }\mathbf{\approx }\mathbf{532} \\ \mathit{\sigma }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{532}}\mathbf{ }\mathbf{\approx }\mathbf{ }\mathbf{23}\mathbf{.}\mathbf{07} \end{gathered}$$

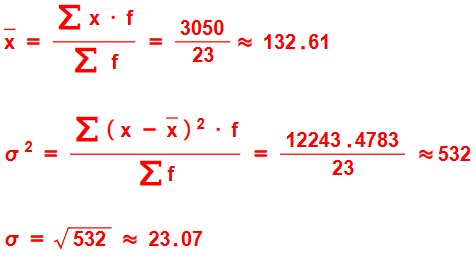
الطريقة الثانية 

$$\begin{gathered} \overline{x} = \frac{\sum _{}x · f}{\sum _{} f} = \frac{3050}{230}\approx 132.61 \\ {\sigma }^{ 2} = \frac{\sum _{} ( x^2 · f) - \left(\sum _{}f \right) {\left(\overline{x}\right)}^2 }{\sum _{} f}= \frac{416700 - \left(23\right){(132.61)}^2}{23} \approx 532 \\ \sigma = \sqrt{532} \approx 23.07 \end{gathered}$$

---

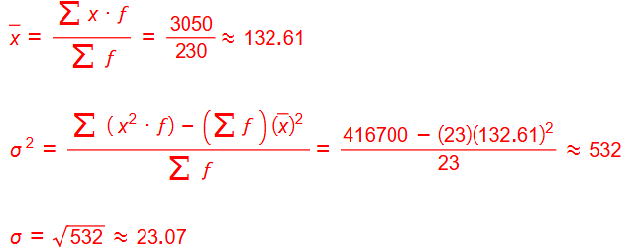
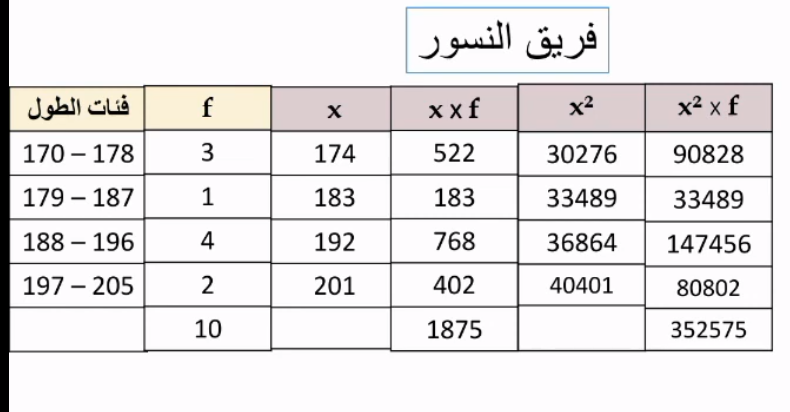
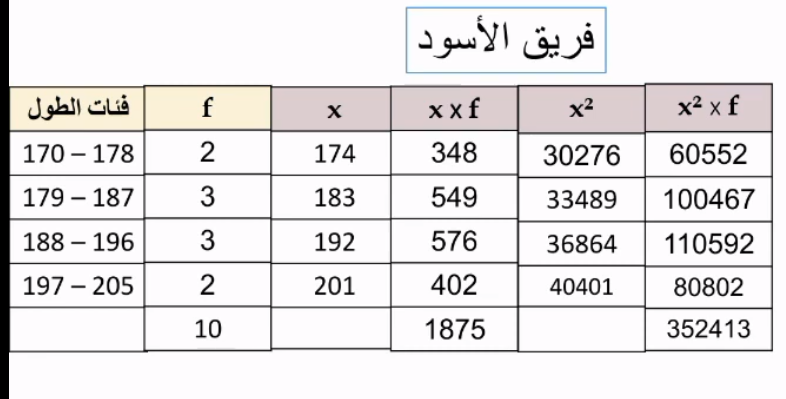
كرة سلة: يبين الجدول المجاور توزيع اللاعبين في فريقين لكرة السلة وفق أطوالهم بالسنتيمتر: 

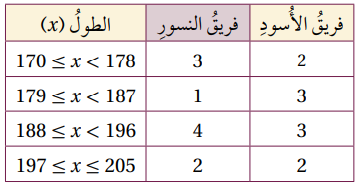
5) أقدر التباين لأطوال اللاعبين في كل فريق 

6) أي الفريقين أكثر تجانسا من أطوال اللاعبين؟ أبرر إجابتي 

5.

$$\begin{gathered} \mathrm{فريق} \mathrm{النسور} 5. 187 = \overline{ x} \\ 10125 ={}^2 \sigma \\ \mathrm{فريق} \mathrm{الأسود} 5. 187 = \overline{x} \\ 05. 85={ }^{ 2 }{\sigma }^{} \end{gathered}$$

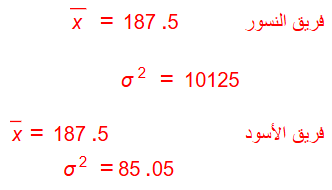
6.

أطول لاعبي فريق الأسود أمثر تجانسا ؛ لأن تباينها أقل من تباين أطوال فريق النسور 

---

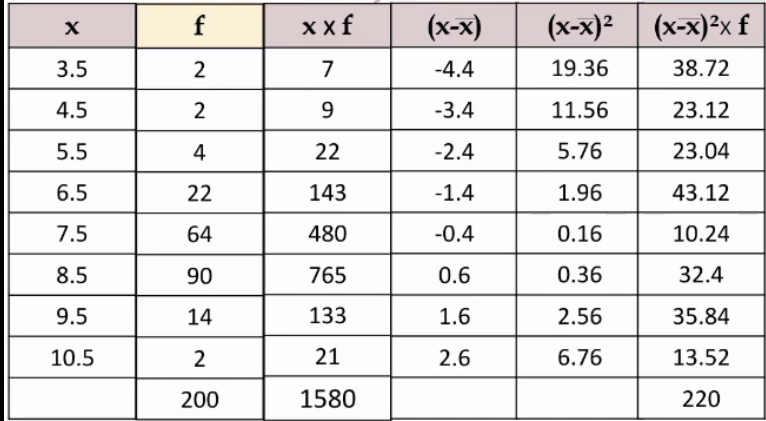
ساعات النوم: يبين التمثيل بالمدرج التكراري المجاور توزيعا ل200 طالب  بحسب ساعات نومهم:

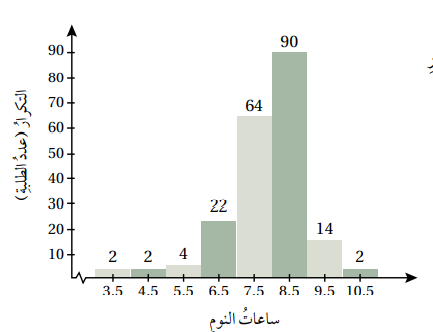
7) أقدر الوسط الحسابي لهذه البيانات

8) أقدر التباين والانحراف المعياري لهذه البيانات 

9) أصف توزيع هذه البيانات 

$$\begin{gathered} 7. \overline{} \\ \overline{x} = 7.9 \\ 8. {\sigma }^{ 2} = \frac{\sum _{}( {\left( x- \overline{x}\right)}^2 \times f)}{\sum _{}f} \\ {\sigma }^{ 2} = 1.1 \\ \sigma = 1.05 \\ 9. \mathrm{اليسار} \mathrm{نحو} \mathrm{ملتو} \mathrm{التوزيع} \end{gathered}$$

---

10) أقارن بين قيمتي التباين للبيانات الممثلة في الشكلين، مفسرا سبب الاختلاف بينهما

 

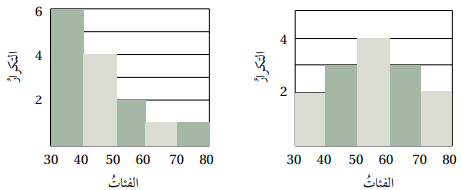
الشكل الأيسر 

الفئات	f	x	X (f)	X2	X2  (f)
40- 30	6	35	210	1225	7350
50 – 40	4	45	180	2025	8100
60 -50	2	55	110	3025	6050
70 -60	1	65	65	4225	4225
80 -70	1	75	75	5625	5625
المجموع			640		31350

 

${\sigma }^{ 2 }= \frac{\sum _{} ( {(x - \overline{x})}^{2 } \times f) }{\sum _{}f}=\frac{31350- \left(14 \times {\left(45.7\right)}^2\right)}{14} =150.8$

 

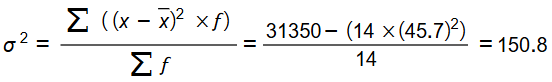
الشكل الأيمن 

 

الفئات	f	x	X (f)	X2	X2  (f)
40- 30	2	35	70	1225	2450
50 – 40	3	45	135	2025	6075
60 -50	4	55	220	3025	12100
70 -60	3	65	195	4225	12675
80 -70	2	75	150	5625	11250
المجموع	14		770		44550

 ${\sigma }^{ 2 } = \frac{44550 - ( 14 \times {\left(55\right)}^2)}{14} =157.14$

  الاختلاف بينهما مرده إلى اختلاف  شكل توزيع البيانات  ؛ ففي الشكل الأيمن تبدو البيانات موزعة طبيعيا ، 
أما في الشكل الأيسر فتوزيع البيانات ملتو نحو اليمين 

---

11) أحل السؤال الوارد في فقرة مسألة اليوم 

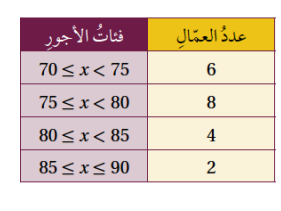
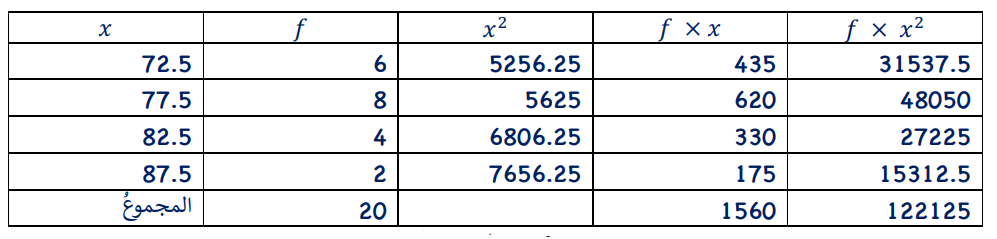
يعمل في مصنع للأثاث المنزلي 20 عاملا، يتوزعومن وفق الأجر الأسبوعي لأقرب دينار كما في الجدول المجاور. في أثناء زيارة مندوب وزارة العمل الذي يتابع أحوال العمال في المصانع، أفاد المدير المالي للمصنع بأن الانحراف المعياري لأجور العاملين هو 4.72 تقريبا. كيف يمكن التحقق من صحة ما أفاد به المدير المالي؟ 

الحل 

$$\begin{gathered} \overline{x} = \frac{\sum _{}x · f}{\sum _{ }f} = \frac{1560}{20} = 78 \\ \sigma { }^{2 } = \frac{\sum _{} ( x^2 · f) - (\sum _{} f) {( \overline{x })}^2}{\sum _{}f} = \frac{122125 - \left(20\right){\left(78\right)}^2}{20} = 22.25 \\ \sigma = \sqrt{22.25} \approx 4.72 \end{gathered}$$

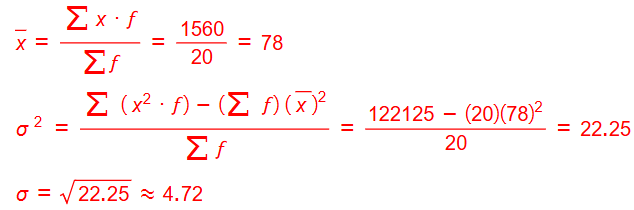
إذا قول المدير المالي صحيح 

 

---

مهارات التفكير العليا 

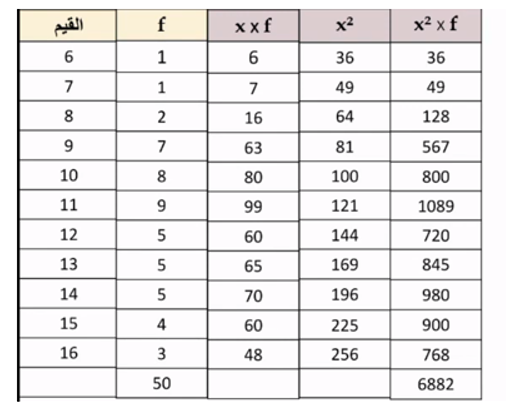
12) مسألة مفتوحة: أنظم البيانات الآتية في جدول تكراري (أختار طولا مناسبا للفترات)، ثم أقدر قيمتي الوسط الحسابي والتباين، مستعملا آلة حاسبة لإيجاد القيمة الدقيقة لكل منهما، ثم أقارن قيمهما الدقيقة بالقيم التقديرية 

 

$$\begin{gathered} \overline{x} = \frac{\sum _{}( x (f\left)\right) }{\sum _{}f}= \frac{575}{50}=11.5 \\ {\sigma }^{ 2}= \frac{\sum _{} ( x^{ 2} \times f) - \left(\sum _{}f\right) {\left(x\right)}^2}{\sum _{}f}= \frac{6923 - 6612.5}{50}= 6.21 \end{gathered}$$

 

$$\begin{gathered} \overline{X} =\frac{\sum _{} x}{n} =\frac{ 574}{50}= 11.48 \\ {\sigma }^{ 2} =\frac{\sum _{}\left( x^2 \times f\right) - \sum _{}f {\left(\overline{x}\right)}^{ 2}}{\sum _{}f} = \frac{6882 - ( 50 \times {\left( 11.48\right)}^2 )}{50} = \frac{6882 - 6589.52}{50}= 5.85 \end{gathered}$$

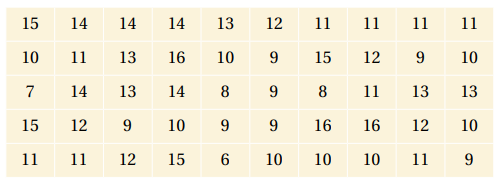
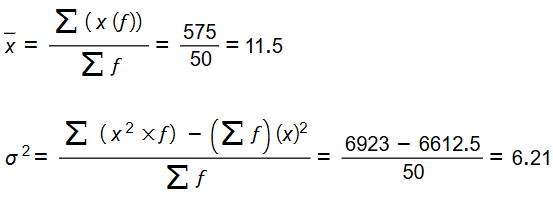
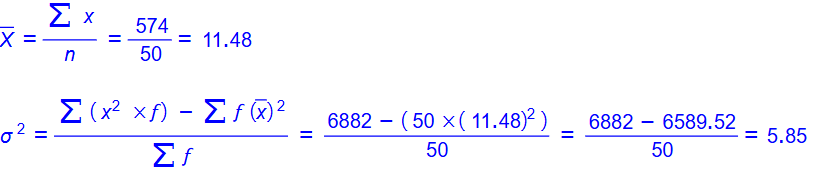
نلاحظ أن قيمة كل من الوسط الحسابي والتباين للطريقتين متقاربة 

---

13) تبرير: في السؤال (12)، ما تأثير أطوال فترات الجدول التكراري الذي أنشأته في القيمة التقديرية للتباين؟ أبرر إجابابتي

 

ستختلف قيمة التباين عن القيمة الدقيقة عند تقديرها بعد تنظيم البيانات في جداول ذات فئات وتكرارات بحسب طول الفئة المتحدة . وكلما زاد طول الفئة قل عدد الفئات في الجدول ، وقلت الدقة في تقدير التباين 

---

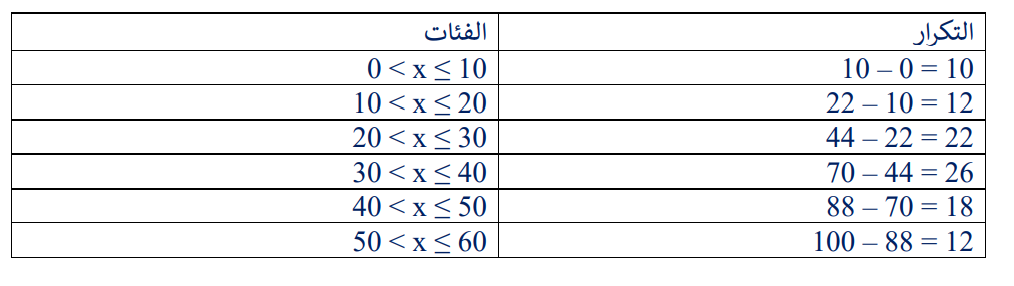
14) تبرير: هل يمكن تقدير التباين للبيانات الممثلة في المنحنى التكراري التراكمي المجاور؟ أبرر إجابتي 

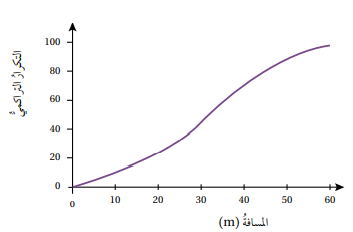
نعم ، يمكن تقدير التباين ؛ لأن حدود الفئات معطاة، ويمكن تحديد التكرار المقابل لكل فئة بطرح التكرار التراكمي السابق من التكرار التراكمي اللاحق والمقابل للحدود العليا للفئات ، ثم إنشاء الجدول على النحو الآتي : 

$\sum _{}{( x - \overline{x})}^2 = \sum _{}\left( x\right)$²  - 2x x  + x ² = ∑  x2 - 2 x ∑x + ∑x  2                                                                                                                                                                          n ∑ x  = n x                                                                                                                                         x = ∑xn ∑ x2 - 2 x ∑x + ∑  x2 =∑x2 -n x  2 = ∑x2 - n ∑x n                                                                                  = ∑x2 - ∑ x 2n

 

15) تبرير: أكتب تبريرا لكل من الخطوات الجبرية الآتية: 

 

$$\begin{gathered} \sum _{ } ( x^2 - 2x \overline{x} - {\left( \overline{x}\right)}^2 ) = \sum _{} x^2 - 2\overline{x } \sum _{}x - n {\overline{x}}^{ 2} \\ = \sum _{} x^2 - 2\overline{x} \sum _{} x + \frac{ n {\left(\sum _{ }x\right)}^2}{n^2} \\ = \sum _{} x^2 - 2\overline{x} \sum _{} x + \frac{{\left(\sum _{} x\right)}^2}{n} \\ = \sum _{ } x^2 -\frac{ 2\sum _{}x }{n} \sum _{}x + \frac{{\left( \sum _{}x\right)}^2}{n} \\ = \sum _{} x^2 - \frac{2{\left( \sum _{}x\right)}^2}{n} + \frac{{\left( \sum _{}x\right)}^2}{n} \\ = \sum _{} x^2 - \frac{{\left( \sum _{}x\right)}^2}{n} \end{gathered}$$

---

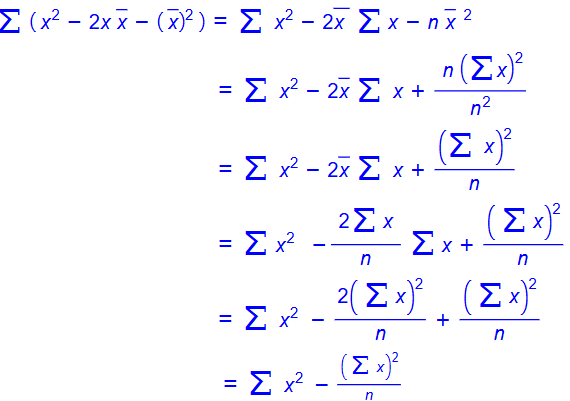
16) أكتب: أي صيغتي التباين أفضل استعمالها؟ 

حل مقترح نفضل الصيغة الثانية لأنها تتطلب خطوات حل أقل من الصيغة الأولى 

---

كتاب التمارين صفحة 27

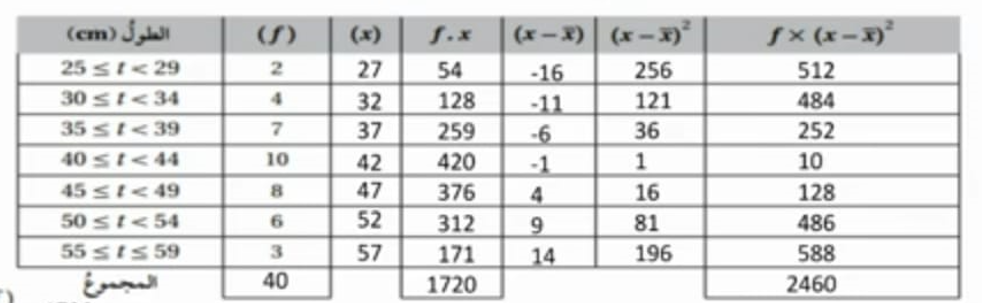
يبين الجدول التكراري الآتي توزيعا لأطوال بعض النباتات  على مدار أسبوع في تجربة زراعية: 

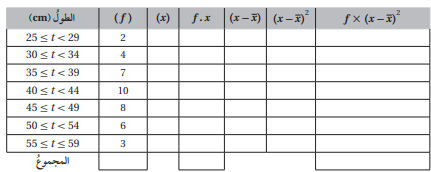
1) أملأ الفراغ بما هو مناسب في الجدول 

2) أقدر  كلا من الوسط الحسابي، والتباين 

$$\begin{gathered} \overline{\mathbf{x}}\mathbf{=}\mathbf{ }\frac{\mathbf{\sum }_{\mathbf{ }}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{\times }\mathbf{f}\mathbf{ }\mathbf{)}}{\mathbf{\sum }_{}\mathbf{ }\mathbf{f}}\mathbf{=}\frac{\mathbf{1720}\mathbf{ }}{\mathbf{40}}\mathbf{=}\mathbf{ }\mathbf{43} \\ {\mathit{\sigma }}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{ }\mathbf{=}\frac{\mathbf{\sum }_{}\mathbf{ }\left( {\left(x - \overline{x}\right)}^2 \times f\right)}{\mathbf{\sum }_{}\mathbf{f}}\mathbf{=}\mathbf{ }\frac{\mathbf{2460}}{\mathbf{40}}\mathbf{=}\mathbf{ }\mathbf{61}\mathbf{.}\mathbf{5} \end{gathered}$$

---

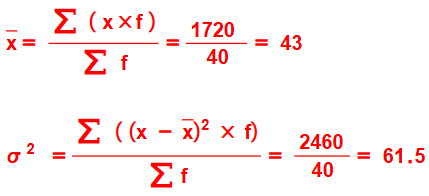
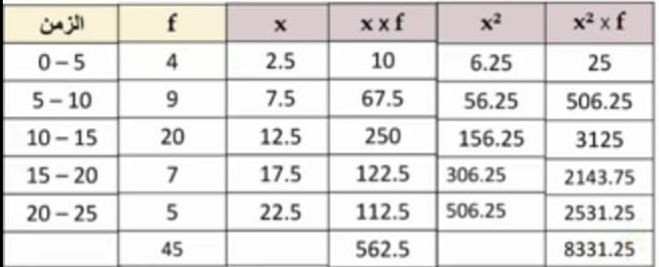
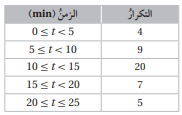
يبين الجدول المجاور توزيع مدة الانتظار t بالدقيقة لعدد من مراجعي دائرة حكومية من لحظة أخذ المراجع بطاقة المراجعة إلى لحظة استدعائه من الموظف المعني:

 

3) أقدر الوسط الحسابي 

$\overline{x}=\frac{\sum _{}\left(x\times f\right)}{\sum _{}f}=\frac{562.5}{45}12.5$

4) أقدر التباين، والانحراف المعياري 

$$\begin{gathered} {\sigma }^{ 2} =\frac{\sum _{}\left(x^{ 2^{}}\times f\right) -\left(\underset{}{\sum f}\right){\left(\overline{x}\right)}^2}{\sum _{}f} =\frac{8331.25-\left(45\times {\left(12.5\right)}^2\right)}{45}=28.9 \\ \sigma =\sqrt{28.9} =5.38 \end{gathered}$$  الانحراف المعياري

---

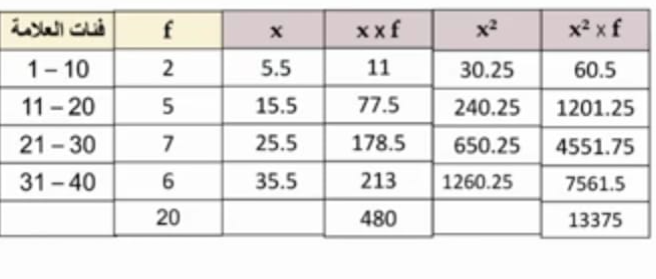
5) مسألة مفتوحة: أجمع بيانات ل20 مشاهدة، وأنظمها في جدول تكراري ذي فئات، ثم أقدر الوسط الحسابي والتباين 

جمع علامات 20 طالب في مادة الرياضيات 

$$\begin{gathered} \overline{\mathbf{x}}\mathbf{ }\mathbf{=}\frac{\mathbf{\sum }_{}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{\times }\mathbf{ }\mathbf{f}\mathbf{)}}{\mathbf{\sum }_{}\mathbf{f}}\mathbf{=}\frac{\mathbf{480}}{\mathbf{20}}\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{24} \\ {\mathit{\sigma }}^{\mathbf{ }\mathbf{2}}\mathbf{ }\mathbf{=}\frac{\mathbf{\sum }_{}\mathbf{ }\mathbf{(}{\left( x- \overline{x}\right)}^{\mathbf{2}\mathbf{ }}\mathbf{\times }\mathbf{ }\mathbf{f}\mathbf{ }\mathbf{)}}{\mathbf{\sum }_{}\mathbf{f}}\mathbf{=}\mathbf{ }\mathbf{92}\mathbf{.}\mathbf{75} \end{gathered}$$

---