مقياس الرسم

مفاهيم أساسية:

مقياسُ الرسمِ ( مقياسُ النموذجِ ): نسبةً تقارنُ بينَ قياساتِ الرسمِ أَوِ النموذجِ وَقياساتِ الأشياءِ الحقيقيةِ، فَقياساتُ الرسمِ أَوِ النموذجِ تتناسبُ مَعَ القياساتِ الحقيقيةِ.

 

يُستعمَلُ مقياسُ الرسمِ لِرسمِ أشكالٍ ثنائيةِ الأبعادِ بِشكلٍ مشابهٍ لِلشكلِ الأصليِّ بِمقاسٍ أكبرَ أَوْ أصغرَ.

مثال 1: يُستعمَلُ ما يقاربُ 700000 زهرةٍ لِتشكيلِ سجادةٍ مستطيلةِ الشكلِ في بلجيكا مرةً كلَّ عامَينِ، وَقبلَ صُنعِ السجادةِ يُعِدُّ المصمِّمونَ مقياسَ رسمٍ لِلسجادةِ. إذا كانَ عَرضُ السجادةِ الحقيقيُّ 40m وَعرضُها على الرسمِ 20cm فَأَجِدُ مقياسَ الرسمِ:

لِإيجادِ مقياسِ الرسمِ أَجِدُ النسبةَ بينَ الطولِ على الرسمِ وَالطولِ الحقيقيِّ، ثمَّ أبسّطُ النسبةَ بحيثُ يصبحُ البسطُ يساوي 1:

$\frac{20\mathrm{cm} \mathrm{الرسم} \mathrm{في} }{40\mathrm{m} \mathrm{الحقيقة} \mathrm{في} }$

$$\begin{gathered} \frac{20÷20}{40÷20} \\ =\frac{1\mathrm{cm}}{2\mathrm{m}}\underset{}{\to }1\mathrm{cm}:2\mathrm{m} \end{gathered}$$                    بالقسمة على 20  بحيثُ يصبحُ البسطُ يساوي 1 والتبسيط

مقياس الرسم يساوي 1cm:2m 

 

يمكنُ استعمالُ مقياسِ الرسمِ لِإيجادِ المسافةِ الفعليةِ بينَ منطقتَينِ بِاستعمالِ الخريطةِ.

مثال 2: تَظهرُ في الشَّكلِ المُجاورِ خَريطةُ المملكةِ الأردنيةِ الهاشميةِ:

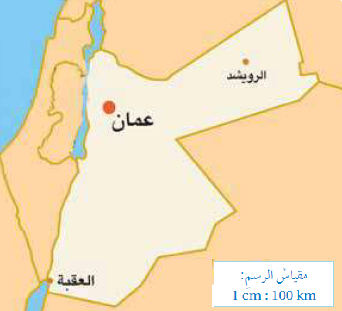
1) أَجِدُ المسافةَ الحقيقيةَ بينَ عمّانَ وَالعقبةِ.

الْخُطْوَةُ 1 : أستعملُ مسطرةَ السنتيمتراتِ لِإيجادِ المسافةِ بينَ عمّانَ وَالعقبةِ على الخريطةِ، وَالّتي تبلغُ 3.3cm تقريبًا.

الْخُطْوَةُ 2: أفترضُ أنَّ المسافةَ الحقيقيةَ بينَ عمّانَ وَالعقبةِ تساوي x ثمّ أكتبُ تناسُبًا مستعمِلً مقياسَ الرسمِ. 

الطول	المقياس
$\frac{3.3\mathrm{cm} \mathrm{الخريطة} \mathrm{على}}{\mathbf{x} \mathrm{الحقيقة} \mathrm{في} }$	$\frac{1\mathrm{cm} \mathrm{الخريطة} \mathrm{على}}{100 \mathrm{Km} \mathrm{الحقيقة} \mathrm{في} } =$

بالضرب التبادلي : 

$$\begin{gathered} 1\times \left(\mathrm{x}\right)=100\times \left(3.3\right) \\ \mathrm{x}=330\mathrm{km} \end{gathered}$$

إذنْ، المسافةُ الحقيقيةُ بينَ عمّانَ وَالعقبةِ تساوي 330km تقريبًا.

 

يُستعمَلُ مقياسُ النموذجِ لِتصميمِ نموذجٍ ثلاثيِّ الأبعادِ مشابِهٍ لِشيءٍ يُرادُ تكبيرُهُ أَوْ تصغيرُهُ. 

مثال3:يبيّنُ الشكلُ المجاورُ نموذجًا لِصاروخِ فضاءٍ استُعمِلَ لِتصميمِهِ مقياسُ النموذجِ 1cm:5m فإذا كانَ ارتفاعُ الصاروخِ 20m فَأَجِدُ ارتفاعَ نموذجِ الصاروخِ.

ثمَّ أكتبُ تناسُبًا مستعمِلًا مقياسَ النموذجِ: ،x أفترضُ أنَّ ارتفاعَ نموذجِ الصاروخِ يساوي

الطول	المقياس
$\frac{\mathbf{x} \mathrm{النموذج} \mathrm{على}}{20\mathrm{m} \mathrm{الحقيقة} \mathrm{في} }$	$\frac{1\mathrm{cm} \mathrm{النموذج} \mathrm{على}}{5\mathrm{m} \mathrm{الحقيقة} \mathrm{في} } =$

باستخدام الضرب التبادلي 

$$\begin{gathered} 1\times \left(20\right)=5\times \left(\mathrm{x}\right) \\ 5\mathrm{x}=20 \\ \mathrm{x}=4\mathrm{cm} \end{gathered}$$

إذنْ، ارتفاعُ نموذجِ الصاروخِ 4cm

 

يمكنُ كتابةُ مقياسِ الرسمِ أَوْ مقياسِ النموذجِ مِنْ دونِ وحداتٍ إذا كانَ للقياساتِ في الحقيقةِ وَفي الرسمِ الوحداتُ نفسُها، وَعندَئذ تُسمّى النسبةُ بينَهُما عاملَ المقياسِ

مثال4:أَجِدُ عاملَ المقياسِ لِنموذجِ سيارةٍ إذا كانَ مقياسُ النموذجِ 1cm:0.5m

$\frac{1\mathrm{cm}}{0.5\mathrm{m}}=\frac{1\mathrm{cm}}{50\mathrm{cm}}$         التحويل من متر الى سنتميتر 

$\frac{1}{50}$                             أختصرُ الوِحداتِ المشترَكةَ

إذنْ، عاملُ المقياسِ 1:50