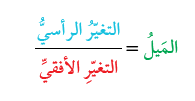
ميلُ المستقيمِ

ميلُ المستقيمِ (slope of a line) هو مصطلحٌ يُستعملُ لوصفِ مقدارِ انحدارِ المستقيمِ. فالمَيلُ هو نسبةُ التغيّرِ الرأسيِّ (rise) إلى التغيّرِ الأفقيِّ (run).

ولإيجادِ ميلِ المستقيمِ غيرِ الرأسيِّ في المستوى الإحداثيِّ يُمكِنُنا إيجادُ نسبةِ التغَيُّرِ في الإحداثيِّ Y (التغَيُّرِ الرأسيِّ) إلى التغَيُّرِ في الإحداثيِّ X (التغَيُّرِ الأفقيِّ) بينَ أيِّ نقطتينِ على المستقيمِ.

للمستقيم المار بالنقطتين $(x_2, y_2) , (x_1, y_1)$

التغير الرأسي $\leftarrow$التغير في $y$ $\leftarrow$ $∆y=y_2-y_1$

التغير الأفقي  $\leftarrow$التغير في $x$ $\leftarrow$ $∆x=x_2-x_1$

الميل $\mathbf{\left(}\mathit{m}\mathbf{\right)}$:               $m = \frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}$

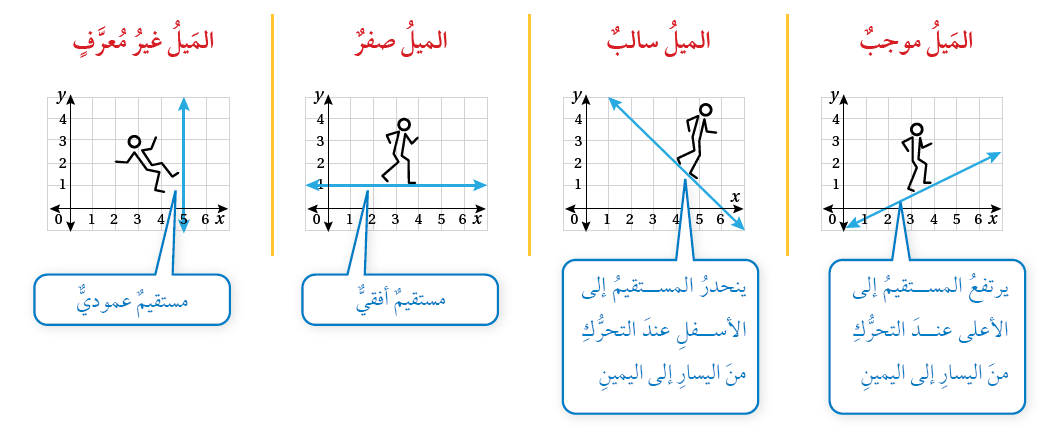
يمكنُ أن يكونَ ميلُ المستقيمِ سالبًا أو موجبًا أو صفرًا أو غيرَ مُعرَّفٍ كما يظهرُ في التمثيلاتِ البيانيةِ أدناهُ. للمقارنةِ بينَ مَيلِ المستقيماتِ المختلفةِ أتخيّلُ نفسي أسيرُ على كلِّ منحنًى منَ اليسارِ إلى اليمينِ:

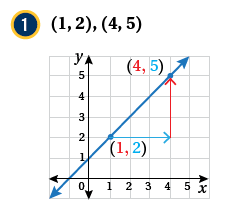
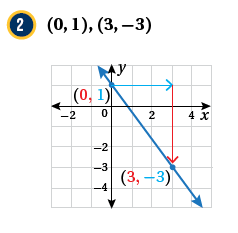
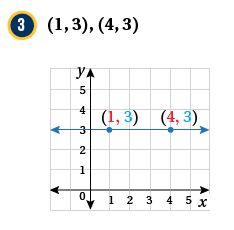
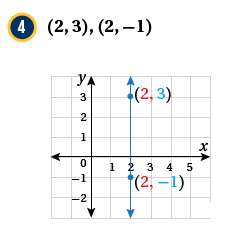
مثال(1)

أجدُ ميلَ المستقيمِ المارِّ بكلِّ نقطتينِ ممّا يأتي:

$$\begin{gathered} (x_1, y_1)\to (1, 2), (x_2, y_2)\to (4, 5) \\ m=\frac{y_2-y_1}{x_2-x_1} \\ = \frac{5-2}{4-1} \\ =\frac{3}{3}=1 \end{gathered}$$

$$\begin{gathered} (x_1, y_1)\to (0, 1), (x_2, y_2)\to (3, -3) \\ m=\frac{y_2-y_1}{x_2-x_1} \\ = \frac{-3-1}{3-0} \\ =\frac{-4}{3} \end{gathered}$$

 

$$\begin{gathered} (x_1, y_1)\to (1, 3), (x_2, y_2)\to (4, 3) \\ m=\frac{y_2-y_1}{x_2-x_1} \\ = \frac{3-3}{4-1} \\ =\frac{0}{3}=0 \end{gathered}$$

 

$$\begin{gathered} (x_1, y_1)\to (2, 3), (x_2, y_2)\to (2, -1) \\ m=\frac{y_2-y_1}{x_2-x_1} \\ = \frac{-1-3}{2-2} \\ =\frac{-4}{0} \end{gathered}$$
الميل غير معرف

إذا عُلِمَ ميلُ المستقيمِ وإحداثيّا نقطةٍ عليهِ، فيمكنُ إيجادُ الإحداثيِّ المجهولِ لأيِّ نقطةٍ أخرى على المستقيمِ.

مثال(2)
أجدُ قيمةَ $s$ التي تجعلُ ميلَ المستقيمِ المارِّ بالنقطتينِ $(-2, 1)$ و $(3, s)$ يساوي $\frac{3}{5}$
$$\begin{gathered} (x_1, y_1)\to (-2, 1), (x_2, y_2)\to (3, s) \\ m=\frac{y_2-y_1}{x_2-x_1} \\ \frac{3}{5}= \frac{s-1}{3-(-2)} \\ \frac{3}{5}=\frac{s-1}{5} \Rightarrow 15 = 5s-5 \\ 5s=20 \\ s= 4 \end{gathered}$$

معدّلُ التغيُّرِ (rate of change) هو نسبةٌ تصفُ مقدارَ تغيّرِ كميةٍ بالنسبةِ إلى تغيرِ كميةٍ أخرى، ويمكنُنا استعمالُ ميلِ المستقيمِ الذي يمثلُ العلاقةَ بينَ هاتينِ الكميتينِ لتفسيرِ معنى معدلِ التغيُّرِ في المسائلِ الحياتيةِ.

 

مثال(3)
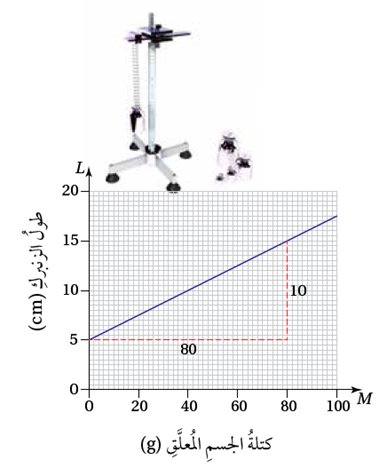
يبيّنُ التمثيلُ البيانيُّ المجاورُ طولَ زنبركٍ بالسنتيمتراتِ، عندَ تعليقِ جسمٍ كتلتُه m غرام بهِ.

1) أجدُ طولَ الزنبركِ قبلَ تعليقِ أيِّ كتلةٍ بهِ. 

طولُ الزنبركِ قبلَ تعليقِ أيِّ كتلةٍ بهِ $5 cm$، وهي القيمةُ التي تقابلُ الكتلةَ $\mathbf{0}\mathbf{ }\mathit{g}$ في التمثيلِ

2) أجدُ معدّلَ تغيرِ طولِ الزنبركِ بالنسبةِ إلى كتلتِه، ثمَّ أبيّنُ ماذا يمثّلُ

لإيجادِ معدلِ التغيّرِ أجدُ ميلَ المستقيمِ الذي يمثّلُ العَلاقةَ بينَ الكتلةِ وطولِ الزنبركِ. أستعملُ النقطتينِ ( 5 , 0) و ( 15 , 80 ) لإيجادِ مَيلِ المستقيمِ.

$$\begin{gathered} (x_1, y_1)\to (0, 5), (x_2, y_2)\to (80, 15) \\ m=\frac{y_2-y_1}{x_2-x_1} \\ = \frac{15-5}{80-0} \\ =\frac{10}{80}=\frac{1}{8} \end{gathered}$$

إذنْ، ميلُ المستقيمِ هو $\frac{1}{8}$، وهو يمثلُ معدّلَ التغيُّرِ في طولِ الزنبركِ لكلِّ غرامٍ منَ الكتلةِ، حيثُ إنَّ طولَ الزنبركِ يزدادُ بمقدار $\frac{1}{8} cm$ لكل غرام يضاف إليه.