رياضيات فصل ثاني

أتحقق من فهمي

ص: 86

أجد قيمة $\tan \theta$ اذا كان $csc \theta =-\frac{3}{2}$، $\mathrm{\pi }<\mathrm{\theta }<\frac{3\mathrm{\pi }}{2}$.

$$\begin{gathered} \sin \left(\theta \right)=\frac{1}{csc\left(\theta \right)}=-\frac{2}{3} \\ si{n}^2\left(\theta \right)+co{s}^2\left(\theta \right)=1 \\ cos\left(\theta \right)=-\frac{\sqrt{5}}{3} \\ tan\left(\theta \right)=\frac{sin\left(\theta \right)}{cos\left(\theta \right)}=\frac{{\displaystyle \frac{-2}{3}}}{{\displaystyle \frac{-\sqrt{5}}{3}}} \\ tan \theta =\frac{2}{\sqrt{5}} \end{gathered}$$

أتحقق من فهمي

ص: 87

أبسط كلا من المقادير المثلثية الآتية:

$a) \sin x(csc x-\sin x)$

$$\begin{gathered} sin x (csc x-sin x)=sin x csc x-si{n}^2 x \\ =sin x \left(\frac{1}{sin x}\right)-si{n}^2 x \\ =1-si{n}^2 x \\ =co{s}^2 x \end{gathered}$$

$b) 1+\frac{\sin x}{\cos x}+\frac{\cos x}{1+\sin x}$

$$\begin{gathered} 1+\frac{sin x}{cos x}+\frac{cos x}{1+sin x}=\frac{cos x (1+sin x)+sin x(1+sin x)+co{s}^2 x}{cos x (1+sin x)} \\ =\frac{cos x (1+sin x)+sin x+si{n}^2 x+co{s}^2 x}{cos x (1+sin x)} \\ =\frac{cos x(1+sin x)+sin x+1}{cos x (1+sin x)} \\ =\frac{(cos x+1)(1+sin x)}{cos x (1+sin x)} \\ =1+sec x \end{gathered}$$

$c) \sin (\frac{\mathrm{\pi }}{2}-x) sec x$

$sin \left(\frac{\mathrm{\pi }}{2}-x\right) sec x=cos x\left(\frac{1}{cos x}\right)=1$

أتحقق من فهمي

ص:87

أعد كتابة $\frac{1}{1+\cos x}$ بحيث لا يحوي كسرًا.

$$\begin{gathered} \frac{1}{1+cos x}=\frac{1 (1-\cos \left(x\right)) }{1+\cos \left(x\right) (1-\cos \left(x\right))}=\frac{1-cosx}{1-co{s}^2 x} \\ =\frac{1-cos x}{si{n}^2 x} \\ =\frac{1}{si{n}^2 x}-\frac{cos x}{sin x}\times \frac{1}{sin x} \\ =cs{c}^2 x-cot x csc x \end{gathered}$$

أتحقق من فهمي

ص: 90

أثبت صحة كل من المتطابقات الآتية:

$a) cot x \cos x=csc x-\sin x$

$$\begin{gathered} cot x cos x=\frac{cos x}{sin x}(cos x) \\ =\frac{co{s}^2 x}{sin x} \\ =\frac{1-si{n}^2 x}{sin x} \\ =\frac{1}{sin x}-sin x \\ =csc x-sin x \end{gathered}$$

$b) \frac{1-\cos x}{\sin x}=\frac{\sin x}{1+ \cos x}$

$$\begin{gathered} \frac{1-cos x}{sin x}=\frac{1-cos x}{sin x}\times \frac{1+cos x}{1+cos x} \\ =\frac{1-co{s}^2 x}{sin x (1+cos x)} \\ =\frac{si{n}^2 x}{sin x (1+cos x)} \\ =\frac{sin x}{1+cos x} \end{gathered}$$

$c) \frac{1}{1-\cos x}+\frac{1}{1+\cos x}=2 cs{c}^{2}x$

$$\begin{gathered} \frac{1}{1-cos x}+\frac{1}{1+cos x}=\frac{(1+cos x)\left(1\right)+(1-cos x)\left(1\right)}{1-co{s}^2 x} \\ =\frac{2}{1-co{s}^2 x} \\ =\frac{2}{si{n}^2 x} \\ =2cs{c}^2 x \end{gathered}$$

أتحقق من فهمي

ص: 90

أثبت صحة المتطابقة: ${(\tan x+ cot x)}^2=se{c}^2 x+cs{c}^2 x$.

$$\begin{gathered} {\left(tan x+cot x\right)}^2={\left(\frac{sin x}{cos x}+\frac{cos x}{sin x}\right)}^2={\left(\frac{si{n}^2 x+co{s}^2 x}{cos x sin x}\right)}^2 \\ ={\left(\frac{1}{cos x sin x}\right)}^2=\frac{1}{co{s}^2 x si{n}^2 x} \\ se{c}^2 x+cs{c}^2 x=\frac{1}{co{s}^2 x}+\frac{1}{si{n}^2 x}=\frac{si{n}^2 x+co{s}^2 x}{co{s}^2 x si{n}^2 x} \\ =\frac{1}{co{s}^2 x si{n}^2 x} \end{gathered}$$

أتحقق من فهمي

ص: 92

أجد قيمة كل مما يأتي من دون استعمال الآلة الحاسبة:

$a) \cos 75°$

$$\begin{gathered} cos 75°=cos(45°+30°) \\ =cos 45° cos 30°-sin 45° sin 30° \\ =\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\times \frac{1}{2}=\frac{\sqrt{3}-1}{2\sqrt{2}} \end{gathered}$$

$b) \tan \frac{\mathrm{\pi }}{12}$

$$\begin{gathered} tan \frac{\mathrm{\pi }}{12}=tan (\frac{\mathrm{\pi }}{3}-\frac{\mathrm{\pi }}{4}) \\ =\frac{tan {\displaystyle \frac{\mathrm{\pi }}{3}}-tan {\displaystyle \frac{\mathrm{\pi }}{4}}}{1+tan {\displaystyle \frac{\mathrm{\pi }}{3}} tan {\displaystyle \frac{\mathrm{\pi }}{4}}} \\ =\frac{\sqrt{3}-1}{1+\sqrt{3}} \end{gathered}$$

$c) \sin 80° \cos 20°-\cos 80° \sin 20°$

$sin 80° cos 20°-cos 80° sin 20°=sin (80°-20°)=sin 60°=\frac{\sqrt{3}}{2}$

أتحقق من فهمي

ص: 93

أثبت صحة كل متطابقة مما يأتي:

$a) \tan \left(\frac{\mathrm{\pi }}{2}-x\right)= cot x$

$tan \left(\frac{\mathrm{\pi }}{2}-x\right)=\frac{sin \left({\displaystyle \frac{\mathrm{\pi }}{2}}-x\right)}{cos \left({\displaystyle \frac{\mathrm{\pi }}{2}}-x\right)}=\frac{cos x}{sin x}=cot x$

$b) \frac{\tan x-1}{\tan x+1}=\tan \left(x-\frac{\mathrm{\pi }}{4}\right)$

$tan \left(x-\frac{\mathrm{\pi }}{4}\right)=\frac{tan x-tan {\displaystyle \frac{\mathrm{\pi }}{4}}}{1+tan x tan {\displaystyle \frac{\mathrm{\pi }}{4}}}=\frac{tan x-1}{1+tan x}$

أتدرب وأحل المسائل

أجد قيمة كل من النسب المثلثية الآتية ضمن الفترة المعطاة:

$1) cot \theta , \sin \theta =\frac{1}{3},0<\theta <\frac{\mathrm{\pi }}{2}$

$$\begin{gathered} co{s}^2\left(\theta \right)+si{n}^2\left(\theta \right)=1 \\ cos\left(\theta \right)=\frac{\sqrt{8}}{3} \\ cot \theta =\frac{cos\left(\theta \right)}{sin\left(\theta \right)}=\frac{{\displaystyle \frac{\sqrt{8}}{3}}}{{\displaystyle \frac{1}{3}}}=\sqrt{8} \end{gathered}$$

$2) sec \theta , \tan \theta =-\frac{3}{7},\frac{\mathrm{\pi }}{2}<\theta <\mathrm{\pi }$

$$\begin{gathered} tan\left(\theta \right)=\frac{sin\left(\theta \right)}{cos\left(\theta \right)}=-\frac{3}{7} \\ sin\left(\theta \right)=-\frac{3}{7}cos\left(\theta \right)..........\left(1\right) \\ si{n}^2\left(\theta \right)+co{s}^2\left(\theta \right)=1 \\ {(-\frac{3}{7}cos\left(\theta \right))}^2+co{s}^2\left(\theta \right)=1 \\ \frac{58}{49}co{s}^2\left(\theta \right)=1 \\ cos\left(\theta \right)=-\frac{7}{\sqrt{58}} \\ sec \theta =\frac{1}{cos\left(\theta \right)}=-\frac{\sqrt{58}}{7} \end{gathered}$$

$3) \tan \theta ,csc \theta =-\frac{5}{3},\mathrm{\pi }<\mathrm{\theta }<\frac{3\mathrm{\pi }}{2}$

$$\begin{gathered} sin\left(\theta \right)=\frac{1}{\csc \left(\theta \right)}=-\frac{3}{5} \\ si{n}^2\left(\theta \right)+co{s}^2\left(\theta \right)=1 \\ {(-\frac{3}{5})}^2+co{s}^2\left(\theta \right)=1 \\ cos\left(\theta \right)=-\frac{4}{5} \\ tan \theta =\frac{\sin \left(\theta \right)}{\cos \left(\theta \right)}=\frac{{\displaystyle \frac{-3}{5}}}{{\displaystyle \frac{-4}{5}}} \\ \tan \left(\theta \right)=\frac{3}{4} \end{gathered}$$

$4) \sin \theta , sec \theta =\frac{9}{4},\frac{3\mathrm{\pi }}{2}<\theta <2\mathrm{\pi }$

$$\begin{gathered} \cos \left(\theta \right)=\frac{1}{\sec \left(\theta \right)}=\frac{4}{9} \\ si{n}^2\left(\theta \right)+co{s}^2\left(\theta \right)=1 \\ {\sin }^2\left(\theta \right)+{\left(\frac{4}{9}\right)}^2=1 \\ \sin \left(\theta \right)=-\frac{\sqrt{65}}{9} \end{gathered}$$

أبسط كلا من العبارات المثلثية الآتية:

$5) \cos x \tan x$

$cos x tan x=cos x \frac{sin x}{cos x}=sin x$

$6) \frac{sec x- \cos x}{\sin x}$

$\frac{sec x-cos x}{sin x}=\frac{{\displaystyle \frac{1}{cos x}}-cos x}{sin x}=\frac{1-co{s}^2 x}{sin x cos x}=\frac{si{n}^2 x}{sin x cos x}=\frac{sin x}{cos x}=tan x$

$7) \frac{\cos \left({\displaystyle \frac{\mathrm{\pi }}{2}}-x\right)}{csc x}+{\cos }^2 x$

$\frac{cos ({\displaystyle \frac{\mathrm{\pi }}{2}}-x)}{csc x}+co{s}^2 x=\frac{sin x}{{\displaystyle \frac{1}{sin x}}}+co{s}^2 x=si{n}^2 x+co{s}^2 x=1$

$8) \frac{\sin x-\cos x}{\cos x}+\frac{\cos x-\sin x}{\sin x}$

$\frac{sin x-cos x}{cos x}+\frac{cos x-sin x}{sin x}=\frac{sin x}{cos x}-\frac{cos x}{cos x}+\frac{cos x}{sin x}-\frac{sin x}{sin x}=tan x+cot x-2$

$9) \frac{{\left(\sin x+\cos x\right)}^2-1}{\sin x \cos x}$

$\frac{{(sin x+cos x)}^2-1}{sin x cos x}=\frac{si{n}^2 x+2sin x cos x+co{s}^2 x-1}{sin x cos x}=\frac{2sin x cos x}{sin x cos x}=2$

$10) \frac{sec x-\cos x}{\tan x}$

$\frac{sec x-cos x}{tan x}=\frac{{\displaystyle \frac{1}{cos x}}-cos x}{{\displaystyle \frac{sin x}{cos x}}}=\frac{1-co{s}^2 x}{sin x}=\frac{si{n}^2 x}{sin x}=sin x$

أثبت صحة كل من المتطابقات الآتية:

$11) cot \left(-x\right) \cos \left(-x\right)+\sin \left(-x\right)=-csc x$

$$\begin{gathered} cot (-x) cos (-x)+sin (-x)=-cot x cos x-sin x \\ =-\frac{cos x}{sin x}(cos x)-sin x \\ =\frac{-co{s}^2 x-si{n}^2 x}{sin x}=\frac{-1}{sin x}=-csc x \end{gathered}$$

$12) {\left(\sin x+\cos x\right)}^2=1+2 \sin x \cos x$

${(sin x+cos x)}^2=si{n}^2 x+2sin x cos x+co{s}^2 x=1+2sin x cos x$

$13) \frac{{\left(\sin x+ \cos x\right)}^2}{{\sin }^2 x-{\cos }^{2}x}=\frac{{\sin }^2 x-{\cos }^2 x}{{\left(\sin x-\cos x\right)}^2}$

$$\begin{gathered} \frac{{(sin x+cos x)}^2}{si{n}^2 x-co{s}^2 x}=\frac{{(sin x+cos x)}^2}{(sin x+cos x)(sin x-cos x)} \\ =\frac{(sin x+cos x)}{(sin x-cos x)}\times \frac{(sin x-cos x)}{(sin x-cos x)}=\frac{si{n}^2 x-co{s}^2 x}{{(sin x-cos x)}^2} \end{gathered}$$

$14) \frac{1-\sin x}{1+\sin x}={\left(sec x-\tan x\right)}^2$

$$\begin{gathered} \frac{1-sin x}{1+sin x}\times \frac{1-sin x}{1-sin x}=\frac{{(1-sin x)}^2}{1-si{n}^2 x} \\ =\frac{{\left(1-sin x\right)}^2}{co{s}^2 x}={\left(\frac{1-sin x}{cos x}\right)}^2={(\frac{1}{\cos \left(x\right)}-\frac{\sin \left(x\right)}{\cos \left(x\right)})}^{2 }={\left(sec x-tan x\right)}^2 \end{gathered}$$

$15) {\sin }^4 x-{\cos }^4 x={\sin }^2 x-{\cos }^2 x$

$si{n}^4 x-co{s}^4 x=(si{n}^2 x-co{s}^2 x)(si{n}^2 x+co{s}^2 x)=si{n}^2 x-co{s}^2 x$

$16) \frac{1}{1-\sin x}-\frac{1}{1+\sin x}=2 sec x \tan x$

$\frac{1}{1-sin x}-\frac{1}{1+sin x}=\frac{1+sin x-1+sin x}{1-si{n}^2 x}=\frac{2 sin x}{co{s}^2 x}=2 tan x sec x$

$17) ln \left|\tan \theta \right|=ln \left|\sin \theta \right|-ln \left|\cos \theta \right|$

$1n\left|tan x\right|=1n\left|\frac{sin x}{cos x}\right|=1n\frac{\left|sin x\right|}{\left|cos x\right|}=1n\left|sin x\right|-1n\left|cos x\right|$

$18) 1n \left|sec \theta +\tan \theta \right|+1n \left|sec \theta -\tan \theta \right|=0$

$$\begin{gathered} 1n\left|sec x+tan x\right|+1n\left|sec x-tan x\right|=1n\left|sec x+tan x\right|\left|sec x-tan x\right| \\ =1n\left|(sec x+tan x)(sec x-tan x)\right| \\ =1n\left|se{c}^2 x-ta{n}^2 x\right|=In 1=0 \end{gathered}$$

أجد قيمة كل من النسب المثلثية الآتية دون استعمال الآلة الحاسبة:

$19) \sin 165°$

$$\begin{gathered} sin 165°=sin 15°=sin(45°-30°)=sin 45° cos 30°-cos 45° sin 30° \\ =\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\times \frac{1}{2}=\frac{\sqrt{3}-1}{2\sqrt{2}} \end{gathered}$$

$20) \tan 195°$

$tan 195°=tan 15°=tan\left(60°-45°\right)=\frac{tan 60°-tan 45°}{1+tan 60° tan 45°}=\frac{\sqrt{3}-1}{1+\sqrt{3}}$

$21) sec \left(-\frac{\mathrm{\pi }}{12}\right)$

$$\begin{gathered} sec \left(-\frac{\mathrm{\pi }}{12}\right)=sec \left(\frac{\mathrm{\pi }}{12}\right)=\frac{1}{cos {\displaystyle \frac{\mathrm{\pi }}{12}}}=\frac{1}{cos \left({\displaystyle \frac{\mathrm{\pi }}{4}}-{\displaystyle \frac{\mathrm{\pi }}{6}}\right)} \\ =\frac{1}{cos {\displaystyle \frac{\mathrm{\pi }}{4}} cos {\displaystyle \frac{\mathrm{\pi }}{6}}+sin {\displaystyle \frac{\mathrm{\pi }}{4}} sin {\displaystyle \frac{\mathrm{\pi }}{6}}} \\ =\frac{1}{{\displaystyle \frac{1}{\sqrt{2}}}\times {\displaystyle \frac{\sqrt{3}}{2}}+{\displaystyle \frac{1}{\sqrt{2}}}\times {\displaystyle \frac{1}{2}}}=\frac{1}{{\displaystyle \frac{\sqrt{3}+1}{2\sqrt{2}}}}=\frac{2\sqrt{2}}{\sqrt{3}+1} \end{gathered}$$

$22) \sin \frac{17\mathrm{\pi }}{12}$

$$\begin{gathered} sin \frac{17\mathrm{\pi }}{12}=-sin \frac{5\mathrm{\pi }}{12}=-sin \left(\frac{\mathrm{\pi }}{4}+\frac{\mathrm{\pi }}{6}\right)=-\left(sin \frac{\mathrm{\pi }}{4} cos \frac{\mathrm{\pi }}{6}+cos\frac{\mathrm{\pi }}{4} sin \frac{\mathrm{\pi }}{6}\right) \\ =-\left(\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}}\times \frac{1}{2}\right)=-\frac{\sqrt{3}+1}{2\sqrt{2}} \end{gathered}$$

$23) \sin \frac{\mathrm{\pi }}{18} \cos \frac{5\mathrm{\pi }}{18}+\cos \frac{\mathrm{\pi }}{18} \sin \frac{5\mathrm{\pi }}{18}$

$sin \frac{\mathrm{\pi }}{18} cos \frac{5\mathrm{\pi }}{18}+cos \frac{\mathrm{\pi }}{18} sin \frac{5\mathrm{\pi }}{18}=sin \left(\frac{\mathrm{\pi }}{18}+\frac{5\mathrm{\pi }}{18}\right)=sin \frac{6\mathrm{\pi }}{18}=sin \frac{\mathrm{\pi }}{3}=\frac{\sqrt{3}}{2}$

$24) \frac{\tan 40°-\tan 10°}{1+\tan 40° \tan 10°}$

$\frac{tan 40°-tan 10°}{1+tan 40° tan 10°}=tan\left(40°-10°\right)=tan 30°=\frac{1}{\sqrt{3}}$

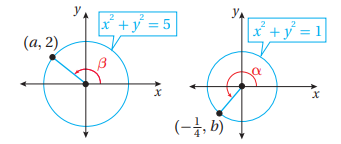
استعمل الشكل المجاور لإيجاد قيمة كل من الاقترانات الآتية، علمًا بأن: $f\left(x\right)=\sin x, g\left(x\right)=\cos x, h\left(x\right)=\tan x$

$25) f(\alpha +\beta )$

$$\begin{gathered} a^2+4=5 \\ a=-1\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \mathrm{النقطة} \mathrm{لأن} \\ {\left(-\frac{1}{4}\right)}^2+b^2=1 \\ b=-\frac{\sqrt{15}}{4} \mathrm{الثالث} \mathrm{الربع} \mathrm{في} \mathrm{النقطة} \mathrm{لأن} \\ sin \alpha =-\frac{\sqrt{15}}{4}, cos \alpha =-\frac{1}{4}, sin \beta =2, cos \beta =-1, tan \alpha =\sqrt{15}, tan \beta =-2 \\ f\left(\alpha +\beta \right)=sin \left(\alpha +\beta \right)=sin \alpha cos \beta +cos \alpha sin \beta =\frac{\sqrt{15}}{4}-\frac{1}{2}=\frac{\sqrt{15}-2}{4} \end{gathered}$$

$26) g(\alpha -\beta )$

$g\left(\alpha -\beta \right)=cos \left(\alpha -\beta \right)=cos \alpha cos \beta +sin \alpha sin \beta =\frac{1-2\sqrt{15}}{4}$

$27) h(\alpha +\beta )$

$h \left(\alpha +\beta \right)= tan \left(\alpha +\beta \right)=\frac{tan \alpha +tan \beta }{1-tan \alpha tan \beta }=\frac{\sqrt{15}-2}{1+2\sqrt{15}}$

28) منشور: يمكن قياس معامل انكسار الضوء الأبيض في المنشور باستعمال المعادلة الآتية: 

$n=\frac{\sin \left({\displaystyle \frac{\theta }{2}}+{\displaystyle \frac{\alpha }{2}}\right)}{\sin {\displaystyle \frac{\theta }{2}}}$

إذا كانت $\alpha =60°$، فأثبت أن معادلة معامل الانكسار تكتب في صورة:

$n=\frac{\sqrt{3}}{2}+\frac{1}{2} cot \frac{\theta }{2}$

$$\begin{gathered} n=\frac{sin \left({\displaystyle \frac{\theta }{2}+\frac{60°}{2}}\right)}{sin {\displaystyle \frac{\theta }{2}}}=\frac{sin \left({\displaystyle \frac{\theta }{2}+30°}\right)}{sin {\displaystyle \frac{\theta }{2}}}=\frac{sin {\displaystyle \frac{\theta }{2}} cos 30°+cos {\displaystyle \frac{\theta }{2}} sin 30°}{sin {\displaystyle \frac{\theta }{2}}} \\ =\frac{{\displaystyle \frac{\sqrt{3}}{2} sin \frac{\theta }{2}+\frac{1}{2} cos \frac{\theta }{2}}}{sin {\displaystyle \frac{\theta }{2}}}=\frac{\sqrt{3}}{2}+\frac{1}{2} cot \frac{\theta }{2} \end{gathered}$$

29) إذا كان g (x) =cos x، فأثبت أن:

$\frac{g(x+h)-g\left(x\right)}{h}=-\cos x\left(\frac{1-\cos h}{h}\right)-\sin x\left(\frac{\sin h}{h}\right)$

$$\begin{gathered} \frac{g(x+h)-g\left(x\right)}{h}=\frac{cos (x+h)-cos \left(x\right)}{h}=\frac{cos x cos h-sin x sin h-cos x}{h} \\ =\frac{cos x cos h-cos x}{h}-\frac{sin x sin h}{h} \\ =-cos x \left(\frac{1-cos h}{h}\right)-sin x \left(\frac{sin h}{h}\right) \end{gathered}$$

30) إذا كان $\sin \left(x+\frac{\mathrm{\pi }}{6}\right)=a \sin x+b \cos x$، فأجد قيمة كل من: a، وb.

$$\begin{gathered} sin \left(x+\frac{\mathrm{\pi }}{6}\right)=sin x cos \frac{\mathrm{\pi }}{6}+cos x sin \frac{\mathrm{\pi }}{6}=\frac{\sqrt{3}}{2}sin x+\frac{1}{2} cos x \\ a=\frac{\sqrt{3}}{2}, b=\frac{1}{2} \end{gathered}$$

أثبت صحة كل من المتطابقات الآتية:

$31) \sin (A+B)+\sin (A-B)=2 \sin A \cos B$

$$\begin{gathered} sin (A+B)+sin (A-B) \\ =sin A cos B+cos A sin B+sin A cos B-cos A sin B=2 sin A cos B \end{gathered}$$

$32) \sin A+\cos A=\sqrt{2} \sin (a+\frac{\mathrm{\pi }}{4})$

$$\begin{gathered} \sqrt{2} sin \left(A+\frac{\mathrm{\pi }}{4}\right)=\sqrt{2} \left(sin A cos \frac{\mathrm{\pi }}{4}+cos A sin \frac{\mathrm{\pi }}{4}\right) \\ =\sqrt{2} \left(\frac{1}{\sqrt{2}} sin A+\frac{1}{\sqrt{2}} cos A\right)=sin A+cos A \end{gathered}$$

$33) \frac{\sin (A-B)}{\cos A \cos B}+\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}=0$

$$\begin{gathered} \frac{sin (A-B)}{cos A cos B}+\frac{sin (B-C)}{cos B cos C}+\frac{sin (C-A)}{cos C cos A} \\ =\frac{sin A cos B-cos A sin B}{cos A cos B}+\frac{sin B cos C-cos B sin C}{cos B cos C}+\frac{sin C cos A-cos C sin A}{cos C cos A} \\ tan A-tan B+tan B-tan C+tan C-tan A=0 \end{gathered}$$

$34) \cos (x+y) \cos (x-y)={\cos }^2 x-{\sin }^2 y$

$$\begin{gathered} cos (x+y) cos (x-y) \\ (\cos x\cos y - \sin x \sin y)(\cos x\cos y + \sin x \sin y) \\ =co{s}^2 x co{s}^2 y-si{n}^2 x si{n}^2 y \\ =co{s}^2 x(1-si{n}^2 y)-(1-co{s}^2 x) si{n}^2 y \\ =co{s}^2 x-co{s}^2 x si{n}^2 y-si{n}^2 y+co{s}^2 x si{n}^2 y \\ =co{s}^2 x-si{n}^2 y \end{gathered}$$

35) جبر: إذا L مستقيما في المستوى الإحداثي، و$\theta$ الزاوية التي يصنعها المستقيم مع المحور x الموجب، فأثبت أن ميل المستقيم m يعطى بالمعادلة $m=\tan \theta$، حيث: $0<\theta <2\mathrm{\pi }$.

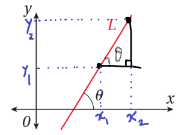
نفرض نقطتين على المستقيم احداثياهما $\left(x_1 , y_1\right) , \left(x_2 , y_2\right)$ كما هو موضح بالشكل،

ميل المستقيم يساوي: $m=\frac{y_2-y_1}{x_2-x_1}$

وظل الزاوية $\theta$ يساوي: $tan \theta =\frac{y_2-y_1}{x_2-x_1}$

اذن ميل المستقيم يساوي ظل زاوية الميل $\theta$

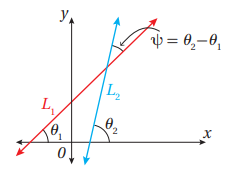
36) إذا كان $L_1$ و $L_2$ مستقيمين غير متوازيين في المستوى الإحداثي، وميل كل منهما $m_1$ و $m_2$ على الترتيب، وكانت $\Psi$ هي الزاوية الناتجة من تقاطع المستقيمين كما في الشكل المجاور، فأستعمل النتيجة من الفرع السابق لإثبات أن:

$\tan \psi =\frac{m_2-m_1}{1+m_1 m_2}$

$$\begin{gathered} \psi ={\theta }_2-{\theta }_1 \\ tan \psi =tan ({\theta }_2-{\theta }_1)=\frac{tan {\theta }_2-tan {\theta }_1}{1+tan {\theta }_2 tan {\theta }_1}=\frac{m_2-m_1}{1+m_2 m_1} \end{gathered}$$

مهارات التفكير العليا

37) تحد: اعتمادًا على الشكل الآتي، أثبت أن: $\alpha +\beta =\gamma$، ثم أجد $\tan \gamma$.

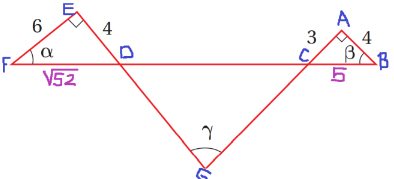
الزاوية ACB والزاوية DCG متقابلتان بالرأس،  وكذلك الزاويتان EDF و CDG، اذن:

قياس الزاوية DCG يساوي $90°-\beta$ وقياس الزاوية CDG يساوي $90°-\alpha$

$$\begin{gathered} Y+90°-\beta +90°-\alpha =180° \\ Y=\alpha +\beta \\ tan Y=tan (\alpha +\beta )=\frac{tan \alpha +tan \beta }{1-tan \alpha tan \beta }=\frac{{\displaystyle \frac{4}{6}}+{\displaystyle \frac{3}{4}}}{1-{\displaystyle \frac{4}{6}}\times {\displaystyle \frac{3}{4}}}=\frac{17}{6} \end{gathered}$$

38) تبرير: إذا كان $\tan \alpha =x+1$، و $\tan \beta =x-1$، فأثبت أن: $2 cot (\alpha -\beta )=x^2$، مبررًا إجابتي.

$$\begin{gathered} 2 cot (\alpha -\beta )=\frac{2}{tan \left(\alpha -\beta \right)}=\frac{2\left(1+tan \alpha tan \beta \right)}{tan \alpha -tan \beta } \\ =\frac{2\left(1+\left(x+1\right)\left(x-1\right)\right)}{\left(x+1\right)-\left(x-1\right)} \\ =\frac{2\left(1+x^2-1\right)}{2} \\ =x^2 \end{gathered}$$

39) تبرير: أجد قيمة $\sin ({\cos }^{-1} \frac{1}{2}+{\sin }^{-1} \frac{1}{\sqrt{2}})$، مبررًا إجابتي.

$$\begin{gathered} sin \left(co{s}^{-1} \frac{1}{2}+si{n}^{-1}\frac{1}{\sqrt{2}}\right)=sin \left(\frac{\mathrm{\pi }}{3}+\frac{\mathrm{\pi }}{4}\right) \\ =sin \frac{\mathrm{\pi }}{3} cos \frac{\mathrm{\pi }}{4}+cos \frac{\mathrm{\pi }}{3} sin \frac{\mathrm{\pi }}{4} \\ =\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{2}}+\frac{1}{2}\times \frac{1}{\sqrt{2}} \\ =\frac{\sqrt{3}+1}{2\sqrt{2}} \end{gathered}$$

40) اكتشف الخطأ: اكتشف الخطأ في المسألة الآتية، ثم أصححه:

 

$$\begin{gathered} \sin (x-\frac{\mathrm{\pi }}{4})=\sin \frac{\mathrm{\pi }}{4}\cos x-\cos \frac{\mathrm{\pi }}{4}\sin x \\ =\frac{\sqrt{2}}{2}\cos x-\frac{\sqrt{2}}{2}\sin x \\ =\frac{\sqrt{2}}{2}(\cos x-\sin x) \end{gathered}$$

 

الخطأ في القانون

الحل الصحيح هو:

$$\begin{gathered} sin \left(x-\frac{\mathrm{\pi }}{4}\right)=sin x cos \frac{\mathrm{\pi }}{4}+cos x sin \frac{\mathrm{\pi }}{4} \\ =\frac{1}{\sqrt{2}} sin x+\frac{1}{\sqrt{2}} cos x \\ =\frac{1}{\sqrt{2}} (sin x+cos x) \end{gathered}$$

أسئلة كتاب التمارين

ابسط كلا من العبارات المثلثية الاتية:

$1) {\cos }^3 x+{\sin }^2 x \cos x$

إخراج cosx عامل مشترك

$cos x$

$2) \frac{1}{1-\cos x}+\frac{1}{1+\cos x}$

توحيد مقام وتجميع حدود

$2 cs{c}^2 x$

$3) \frac{se{c}^2 x-1}{se{c}^2 x}$

متطابقات

$si{n}^2 x$

$4) \frac{{\cos }^2 x-1}{{\cos }^2 x-\cos x}$

تحليل البسط وإخراج عامل مشترك من المقام

$1+sec x$

$5) \frac{1+\cos x}{1+sec x}$

متطابقة sec وتوحيد مقام واختصار

$cos x$

$6) \frac{3 {\sin }^2 x+4 \sin x+1}{{\sin }^2 x+2 \sin x+1}$

تحليل ثلاثي حدود ثم اختصار (sin x+ 1)

$\frac{3 sin x+1}{sin x+1}$

أثبت صحة كل من المتطابقات الاتية:

$7) \frac{\cos x}{sec x}+\frac{\sin x}{csc x}=1$

$\frac{cos x}{sec x}+\frac{sin x}{csc x}=co{s}^2 x+si{n}^2 x=1$

$8) 1n\left|1+\cos \theta \right|+1n\left|1-\cos \theta \right|=2 1n\left|\sin \theta \right|$

$$\begin{gathered} ln\left|1+cos x\right|+ln\left|1-cos x\right|=ln\left|(1+cos x)(1-cos x)\right| \\ =ln\left|1-co{s}^2 x\right|=ln\left|si{n}^2 x\right|=2 ln\left|sin x\right| \end{gathered}$$

$9) \frac{1}{1-{\sin }^2 x}=1+{\tan }^2 x$

$\frac{1}{1-si{n}^2 x}=\frac{1}{co{s}^2 x}=se{c}^2 x=1+ta{n}^2 x$

$10) \tan A+\tan B=\frac{\sin (A+B)}{\cos A \cos B}$

$\frac{sin\left(A+B\right)}{cos A cos B}=\frac{sin A cos B+cos A sin B}{cos A cos B}=\frac{sin A}{cos A}+\frac{sin B}{cos B}=tan A+tan B$

أجد قيمة كل من النسب المثلثية الاتية من دون استعمال الالة الحاسبة:

$11) \sin 105°$

$sin 105°=\sin \left(60°+45°\right)=\frac{1+\sqrt{3}}{2\sqrt{2}}$

$12) \tan \frac{19\mathrm{\pi }}{12}$

$tan \frac{19\mathrm{\pi }}{12}=-2-\sqrt{3}$

$13) \cos 10° \cos 80°-\sin 10° \sin 80°$

$cos (10°+80°) = \cos \left(90°\right)=0$

14) اذا كان $\sin x+\sin (x+\frac{\mathrm{\pi }}{6})=\sin (x+\frac{\mathrm{\pi }}{3})$، فأثبت أن: $\tan x=2-\sqrt{3}$.

$$\begin{gathered} sin x+sin \left(x+\frac{\mathrm{\pi }}{6}\right)=sin \left(x+\frac{\mathrm{\pi }}{3}\right) \\ sin x+sin x cos\frac{\mathrm{\pi }}{6}+cos x sin \frac{\mathrm{\pi }}{6}=sin x cos \frac{\mathrm{\pi }}{3}+cos x sin \frac{\mathrm{\pi }}{3} \\ sin x+\frac{\sqrt{3}}{2}sin x+\frac{1}{2}cos x =\frac{1}{2} sin x+\frac{\sqrt{3}}{2} cos x \\ \frac{1+\sqrt{3}}{2} sin x=\frac{\sqrt{3}-1}{2} cos x \\ tan x=2-\sqrt{3} \end{gathered}$$

15) اذا كان $A+B=\frac{\mathrm{\pi }}{4}$، فأثبت أن: $\tan A=\frac{1-\tan B}{1+\tan B}$.

$tan A=tan \left(\frac{\mathrm{\pi }}{4}-B\right)=\frac{tan {\displaystyle \frac{\mathrm{\pi }}{4}}-tan B}{1+tan {\displaystyle \frac{\mathrm{\pi }}{4}} tan B}=\frac{1-tan B}{1+tan B}$

16) تبرير: أثبت صحة المتطابقة: $\tan (s+t)=\frac{\sin (s+t)}{\cos (s+t)}$، مبررًا اجابتي.

$$\begin{gathered} tan \left(s+t\right)=\frac{tan s+tan t}{1-tan s tan t}=\frac{{\displaystyle \frac{sin s}{cos s}}+{\displaystyle \frac{sin t}{cos t}}}{1-{\displaystyle \frac{sin s}{cos s}}\times {\displaystyle \frac{sin t}{cos t}}} \\ =\frac{sin s cos t+cos s sin t}{cos s cos t-sin s sin t}=\frac{sin \left(s+t\right)}{cos \left(s+t\right)} \end{gathered}$$

17) تبرير: يبين التمثيل البياني الاتي منحنيي الاقترانين: $y={\sin }^2 x$، و $y={\cos }^2 x$، حيث الزوايا بالدرجات. أستعمل هذا التمثيل لاثبات أن: ${\cos }^2 \theta +{\sin }^2 \theta =1$

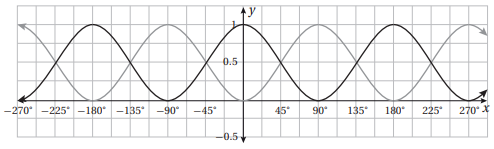
من التمثيل البياني نلاحظ ان المنحنيين متماثلين حول المستقيم الذي معادلته y = 1/2

من خلال الرسم يوجد ثلاث وضعيات للرسم 

1) اذا كان منحنى $y=si{n}^2 \theta$ فوق منحنى $y={\cos }^2 \theta$:

نكتب: $co{s}^2 \theta -\frac{1}{2}=\frac{1}{2}-si{n}^2 \theta$ 

ومنه $si{n}^2 \theta +co{s}^2 \theta =1$

2) اذا كان منحنى $y=co{s}^2 \theta$ فوق منحنى $y={\sin }^2 \theta$:

نكتب: $co{s}^2 \theta -\frac{1}{2}=\frac{1}{2}-si{n}^2 \theta$ 

ومنه $si{n}^2 \theta +co{s}^2 \theta =1$

3) عند تقاطع التقاطع فان $co{s}^2 \theta =\frac{1}{2} و si{n}^2 \theta =\frac{1}{2}$ 

ومنه $si{n}^2 \theta +co{s}^2 \theta =1$ 

أي أنه أيًا كان قياس الزاوية $\theta$ فان $si{n}^2 \theta +co{s}^2 \theta =1$ وهو المطلوب.