يُسمى الاقتران الذي يحوي قيمة مطلقة لمقدار جبري اقتران القيمة المطلقة، ومن أمثلته :
• يُمكن إعادة كتابة اقتران القيمة المطلقة في صورة اقتران متشعب، من دون استعمال رمز القيمة المُطلقة، وهو ما يُسمى إعادة تعريف اقتران القيمة المطلقة.
مثال 1
أُعيد تعريف اقتران القيمة المطلقة | f(x) = |2x - 4 ، ثم أجد كل من f(-1) و f(3) و f(2)
الحل :
لإعادة تعريف اقتران القيمة المطلقة، أتبع الخطوات الآتية :
الخطوة 1 : أجعل ما في داخل القيمة المطلقة يساوي صفرًا، ثم أحل المعادلة الناتجة.
الخطوة 2 : أُعين جذر المعادلة على خط الأعداد، ثم أُحدد الإشارة على جانبية.
أُعين العدد 2 على خط الأعداد، ثم أحدد الإشارة على جانبيه، بتعويض أي قيمة أقل من 2 (مثل 0) في المقدار الجبري : ، فيكون دائما ناتج التعويض سالبًا؛ ما يعني أنّ إشارة المقدار سالبة يسار العدد 2، بعد ذلك أُعوض أي قيمة أكبر من 2 (مثل 3) في المقدار الجبري:ويكون دائما ناتج التعويض موجبًا؛ ما يعني أنّ إشارة المقدار موجبة يمين العدد 2
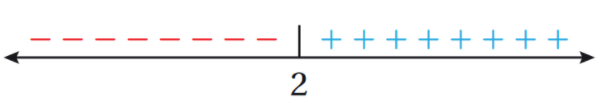
الخطوة 3 : أكتب قاعدتي الاقتران بحسب إشارة يمين صفر المعادلة ويساره.
أكتب ما في داخل رمز القيمة المطلقة كما هو من دون تغيير في الجزء الموجب، ثم أكتب في الجزء السالب ما في داخل رمز القيمة المطلقة مضروبا في 1 -
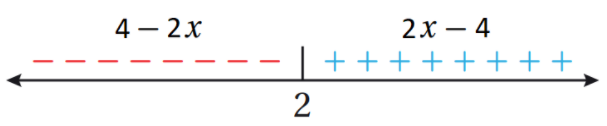
الخطوة 4 : أكتب قاعدة الاقتران المتشعب (من دون استعمال رمز القيمة المطلقة).
ويمكن كتابة الاقتران على النحو التالي:
حيث يُمكن وضع إشارة المساواة عند أي من الفترتين ، ولكن جرت العادة وضعها عند رمز أكبر(x ≥ )