فكرة الدرس : تعرّف اقتران القيمة المطلقة، وتمثيله بيانيًا، وتحديد مجاله ومداه.
يُسمى الاقتران الذي يحوي قيمة مطلقة لمقدار جبري اقتران القيمة المطلقة، ومن أمثلته:
تعلمت سابقًا أن القيمة المطلقة (يُرمز إليها بالرمز |x|) لأي عدد حقيقي x تساوي بُعده عن الصفر على خط الأعداد.
وبما أن البعد لا يكون سالبًا، فإنّ ؛ لذا يُمكن كتابة |x| في صورة اقتران متشعب كما يأتي:
• يُمكن أيضًا إعادة كتابة اقتران القيمة المطلقة في صورة اقتران متشعب، من دون استعمال رمز القيمة المُطلقة، وهو ما يُسمى إعادة تعريف اقتران القيمة المطلقة.
مثال1
أُعيد تعريف اقتران القيمة المطلقة f(x) = |2x - 4|، ثم أجد كل من f(-1) و f(3) و f(2)
الحل :
لإعادة تعريف اقتران القيمة المطلقة، أتبع الخطوات الآتية:
الخطوة 1 : أجعل ما في داخل القيمة المطلقة يساوي صفرًا، ثم أحل المعادلة الناتجة.
الخطوة 2 : أُعين جذر المعادلة على خط الأعداد، ثم أُحدد الإشارة على جانبية.
أُعين العدد 2 على خط الأعداد، ثم أحدد الإشارة على جانبيه، بتعويض أي قيمة أقل من 2 (مثل 0) في المقدار الجبري : ، فيكون دائما ناتج التعويض سالبًا؛ ما يعني أنّ إشارة المقدار سالبة يسار العدد 2، بعد ذلك أُعوض أي قيمة أكبر من 2 (مثل 3) في المقدار الجبري: ، ويكون دائما ناتج التعويض موجبًا؛ ما يعني أنّ إشارة المقدار موجبة يمين العدد 2 :
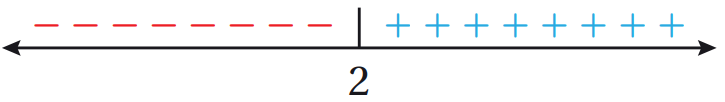
الخطوة 3 : أكتب قاعدتي الاقتران بحسب إشارة يمين صفر المعادلة ويساره.
أكتب ما في داخل رمز القيمة المطلقة كما هو من دون تغيير في الجزء الموجب، ثم أكتب في الجزء السالب ما في داخل رمز القيمة المطلقة مضروبا في 1 -
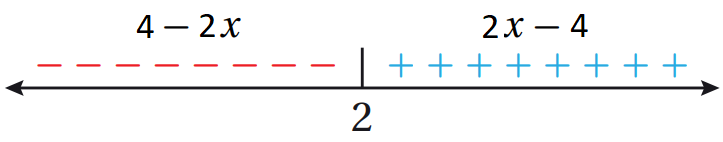
الخطوة 4 : أكتب قاعدة الاقتران المتشعب (من دون استعمال رمز القيمة المطلقة).
ويمكن كتابة الاقتران على النحو التالي:
حيث يُمكن وضع إشارة المساواة عند أي من الفترتين ، ولكن جرت العادة وضعها عند رمز أكبر(x ≥ )
لإيجاد كل من : ،أعوّض في القاعدة المناسبة:
• التمثيل البياني لاقتران القيمة المطلقة في صورة: ، حيثُ: يتكون من شعاعين على شكل ꓦ أو ꓥ متماثلين حول المحور: .
رأس منحنى الاقتران هو النقطة التي يصل عندها منحناه إلى أعلى قيمة أو أقل قيمة، وإحداثياها.
يُمكن تمثيل اقتران القيمة المطلقة بيانيا باستعمال محور التماثل والرأس.
مثال
مثّل بيانيا الاقتران ، محددًا مجاله ومداه.
الحل:
الخطوة 1 : أجد إحداثيي نقطة رأس الاقتران، ومعادلة محور التماثل.
أُقارن الاقتران: بالصيغة: ، فأُلاحظ أنّ:
- أجد إحداثيي نقطة الرأس:
إحداثيا نقطة الرأس
بتعويض
بالتبسيط
- أجد معادلة محور التماثل:
معادلة محور التماثل
بتعويض
بالتبسيط
الخطوة 2 : أُحدد قيمتين للمتغير x حول محور التماثل، ثم أجد صورة كلّ منهما.
بما أنّ محور التماثل: x = 1 ، فإنّني أختار قيمة للمتغير x أكبر من 1 (مثل 2)، وقيمة أخرى أقل من 1 (مثل ( 0 ، ثم أجد صورتيهما في الاقتران كما في الجدول الآتي:
|
2 |
0 |
x |
|
1 |
1 |
f(x) = |x – 1| |
|
(2 , 1) |
(0 , 1) |
(x , y) |
الخطوة 3 : أُمثل الاقتران بيانيًا
أُمثل النقطتين والرأس في المستوى الإحداثي، ثم أصل بين النقاط الثلاث على شكل ꓦ.
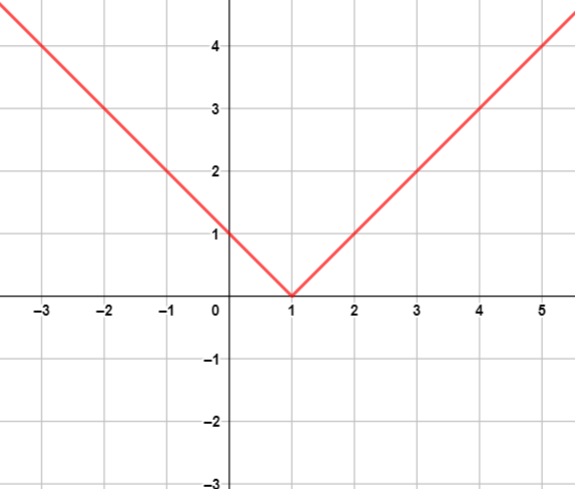
أُلاحظ من التمثيل البياني أنّ المجال هو مجموعة الأعداد الحقيقية، وأنّ المدى هو:
• يمكن إيجاد قاعدة اقتران القيمة المطلقة لمقدار خطي إذا أُعطي تمثيله البياني.
| مثال: | 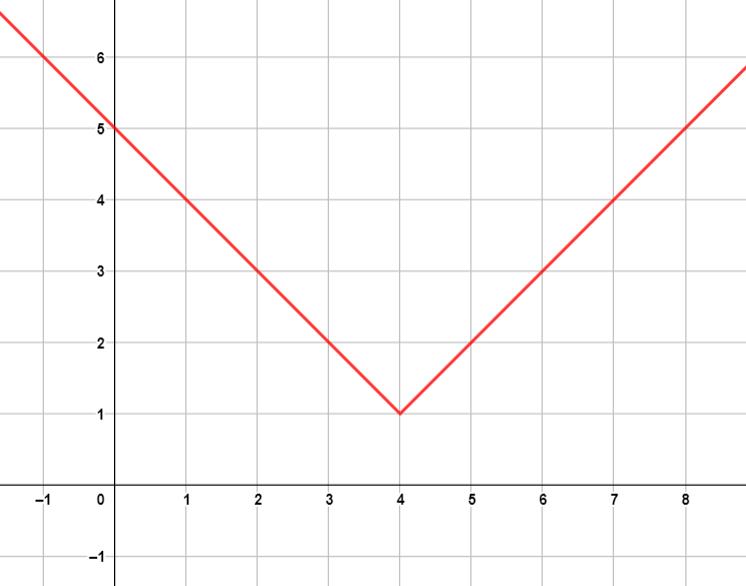 |
| أكتب قاعدة اقتران القيمة المطقة المُمثل بيانيًا في الشكل المجاور. | |
| الخطوة 1: أجد ميل المعادلة الخطية داخل رمز المطلق. | |
|
يتبين من الشكل أنّ التمثيل البياني هو لاقتران قيمة مطلقة خطي؛ لأنه على |
|
| شكل V ؛ لذا يُمكن كتابة قاعدتهُ كما يأتي: | |
| ، حيث m ميل المستقيم: y = mx + b |
أُلاحظ من التمثيل البياني أنّ الشعاع الأيمن يمر بالنقطتين وبذلك فإن ميله:
الخطوة 2 : أجد إحداثي الرأس، ثم أُعوض الميل وإحداثيي الرأس في قاعدة الاقتران.
إحداثيا الرأس هما: ، والتمثيل البياني يُظهر أنّ النقطة تُمثل رأس الاقتران.
بالمقارنة، أستنتج أن c = 1 ، ثم أجد قيمة b من الإحداثي x للرأس:
بتعويض قيمة كل من: m , b , c في قاعدة الاقتران، فإنّ:
الخطوة 3 : أجد قيمة a
لإيجاد قيمة a، أعوض في قاعدة الاقتران الناتجة من الخطوة السابقة إحداثيي نقطة تقع على منحنى الاقتران، ثم أحلُّ المعادلة الناتجة:
لتكن النقطة (0 , 5)
إذن، قاعدة الاقتران هي: