حلول أسئلة كتاب الطالب وكتاب التمارين
حلول أسئلة أتحقق من فهمي
اتحقق من فهمي صفحة 16
أُعيد تعريف اقتران القيمة المطلقة:
الحل:
- أجعل ما في داخل القيمة المطلقة يساوي صفرًا، ثم أحل المعادلة الناتجة.
- أُعين جذر المعادلة على خط الأعداد، ثم أُحدد الإشارة على جانبية.
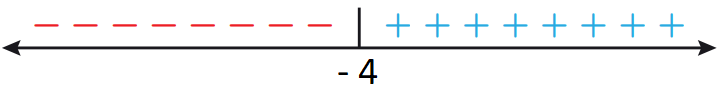
-أكتب قاعدتي الاقتران بحسب إشارة يمين صفر المعادلة ويساره.
أكتب ما في داخل رمز القيمة المطلقة كما هو من دون تغيير في الجزء الموجب، ثم أكتب في الجزء السالب ما في داخل رمز القيمة المطلقة مضروبا في :
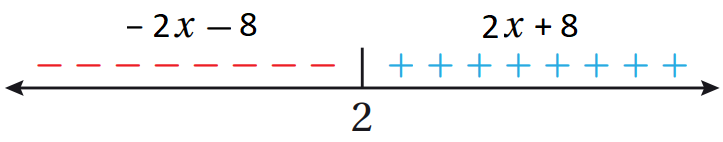
- أكتب قاعدة الاقتران المتشعب (من دون استعمال رمز القيمة المطلقة).
أتحقق من فهمي صفحة 19
أُمثل بيانيًا كل اقتران ممّا يأتي، مُحددا مجاله ومداه:
الحل:
الخطوة 1 : أجد إحداثيي نقطة رأس الاقتران، ومعادلة محور التماثل.
أُقارن الاقتران: بالصيغة: ، فأُلاحظ أنّ:
- أجد إحداثيي نقطة الرأس:
إحداثيا نقطة الرأس
بتعويض
بالتبسيط
- أجد معادلة محور التماثل:
معادلة محور التماثل
بتعويض
بالتبسيط
الخطوة 2 : أُحدد قيمتين للمتغير x حول محور التماثل، ثم أجد صورة كلّ منهما.
|
1 |
-1 |
x |
|
-2 |
-2 |
F(x) = - |2x| |
|
(1 , -2) |
(-1 , -2) |
(x , y) |
الخطوة 3 : أُمثل النقطتين والرأس في المستوى الإحداثي، ثم أصل بين النقاط الثلاث على شكل ꓦ.
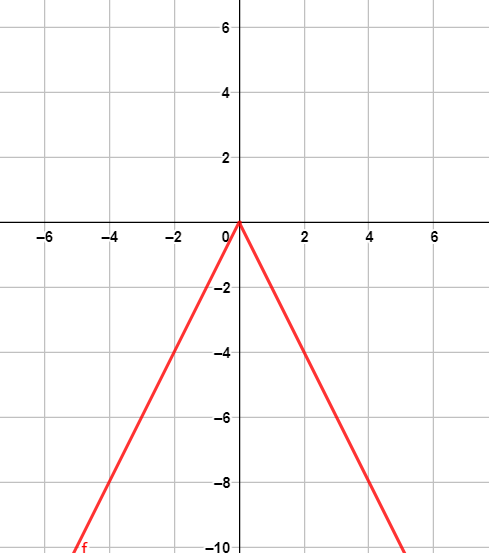
المجال: مجموعة الأعداد الحقيقية، المدى:
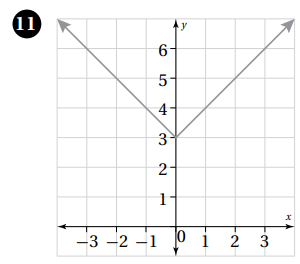
الخطوة 1 : أجد إحداثيي نقطة رأس الاقتران، ومعادلة محور التماثل.
أُقارن الاقتران: بالصيغة: ، فأُلاحظ أنّ:
- أجد إحداثيي نقطة الرأس:
إحداثيا نقطة الرأس
بتعويض
بالتبسيط
- أجد معادلة محور التماثل:
معادلة محور التماثل
بتعويض
بالتبسيط
الخطوة 2 : أُحدد قيمتين للمتغير x حول محور التماثل، ثم أجد صورة كلّ منهما.
|
4 |
2 |
x |
|
3 |
3 |
F(x) = |x – 3|+2 |
|
(4 , 3) |
(2 , 3) |
(x , y) |
الخطوة 3 : أُمثل النقطتين والرأس في المستوى الإحداثي، ثم أصل بين النقاط الثلاث على شكل ꓦ .
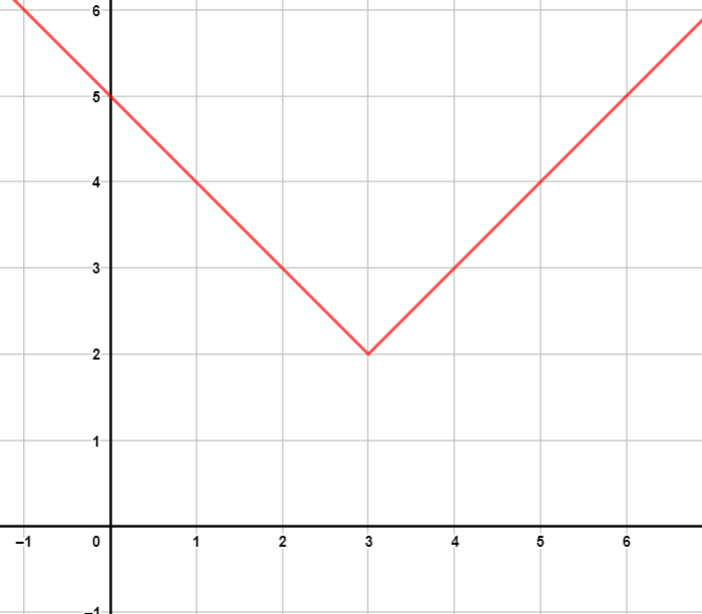
المجال: مجموعة الأعداد الحقيقية، المدى:
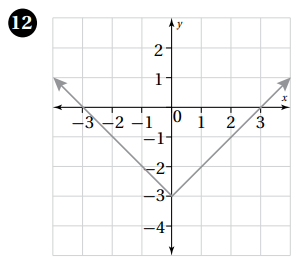
| أتحقق من فهمي صفحة 20 | 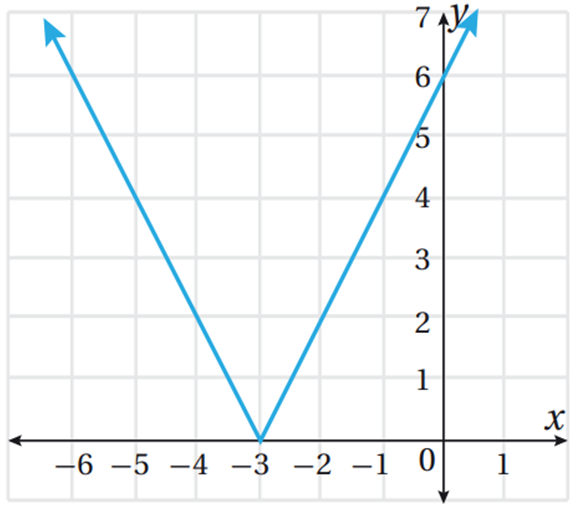 |
| أكتب قاعدة اقتران القيمة المطلقة المُمثل بيانيًا في الشكل المجاور. | |
| الخطوة 1 :أجد ميل المعادلة الخطية داخل رمز المطلق. | |
| يتبين من الشكل أنّ التمثيل البياني هو لاقتران قيمة مطلقة خطي؛ | |
| لأنه على شكل V؛ لذا يُمكن كتابة قاعدتهُ كما يأتي: | |
| ، حيث m ميل المستقيم: y = mx + b |
أُلاحظ من التمثيل البياني أنّ الشعاع الأيمن يمر بالنقطتين ، وبذلك فإن ميله:
الخطوة 2 : أجد إحداثي الرأس، ثم أُعوض الميل وإحداثيي الرأس في قاعدة الاقتران.
إحداثيا الرأس هما: ، والتمثيل البياني يُظهر أنّ النقطة تُمثل رأس الاقتران.
بالمقارنة، أستنتج أن c = 0 ، ثم أجد قيمة b من الإحداثي x للرأس:
بتعويض قيمة كل من: m , b , c في قاعدة الاقتران، فإنّ:
الخطوة 3 : أجد قيمة a
لإيجاد قيمةa ، أعوض في قاعدة الاقتران الناتجة من الخطوة السابقة إحداثيي نقطة تقع على منحنى الاقتران، ثم أحلُّ المعادلة الناتجة:
لتكن النقطة (0 , 6)
إذن، قاعدة الاقتران هي:
حلول أسئلة أتدرب وأحل المسائل
أعيدُ تعريف كل من الاقترانات الآتية:
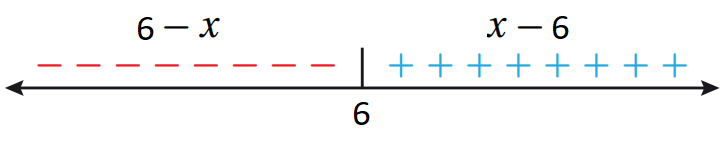 |
|
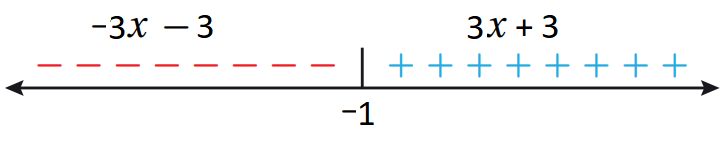 |
|
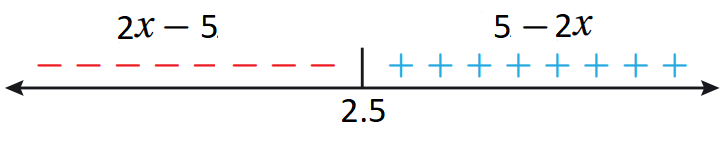 |
|
|
ملاحظة: في هذه الحالة يُعاد تعريف القيمة المُطلقة |
|
|
كالمُعتاد، ويُضاف للقواعد العدد 3
|
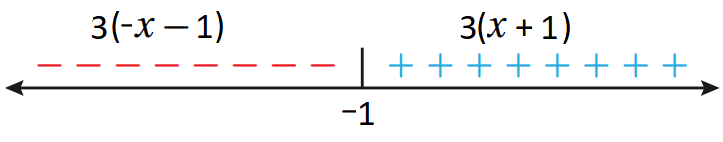 |
|
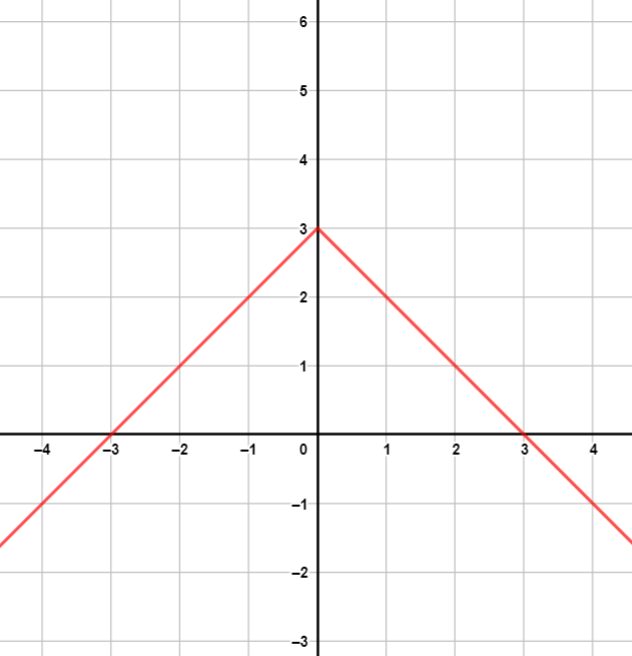
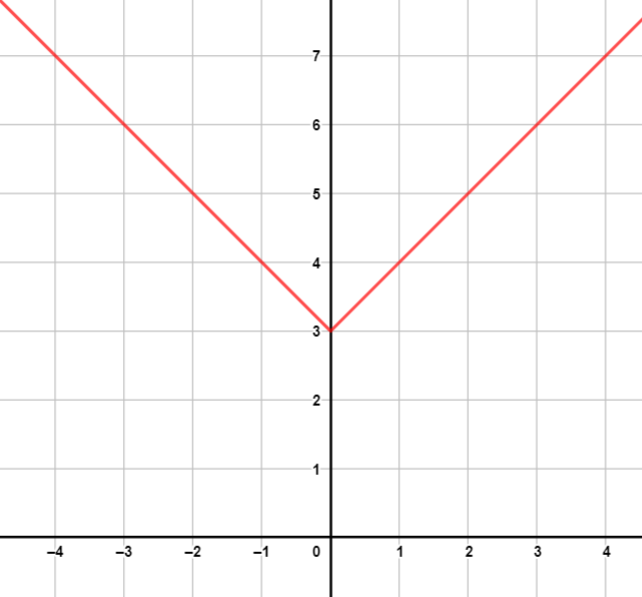
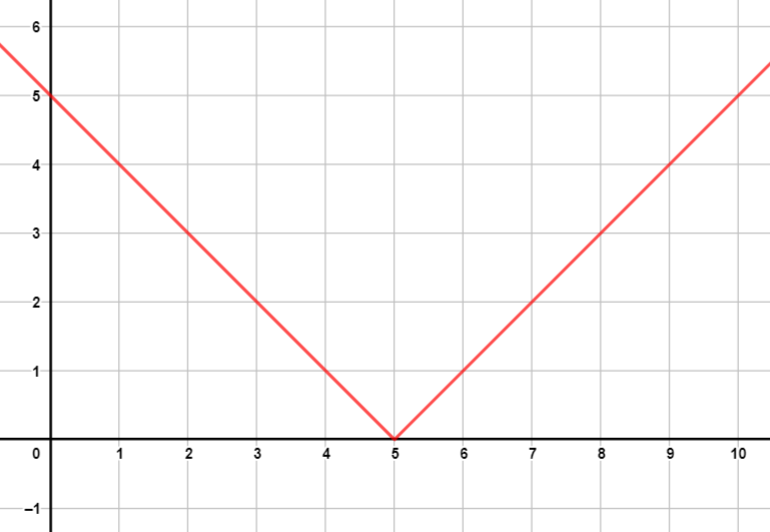
أُمثل بيانيًا كل اقتران مما يأتي، مُحددًا مجاله ومداه:
 |
 |
|
| المجال: ، المدى: |
المجال: ، المدى: |
 |
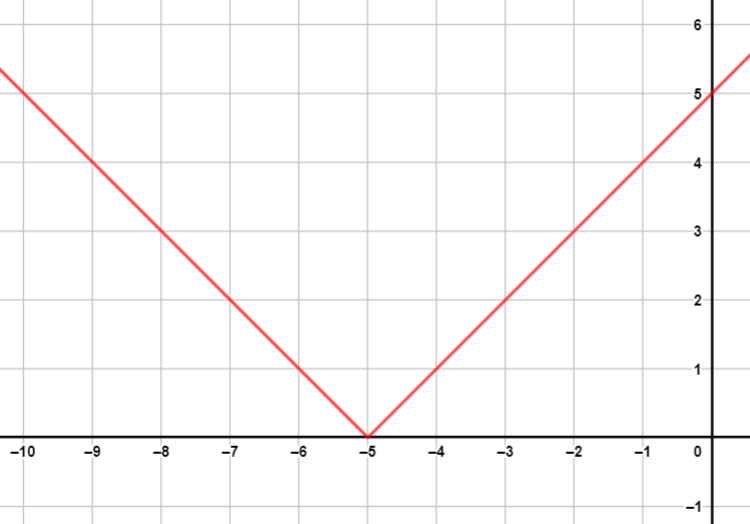 |
|
| المجال: ، المدى: | المجال: ، المدى: |
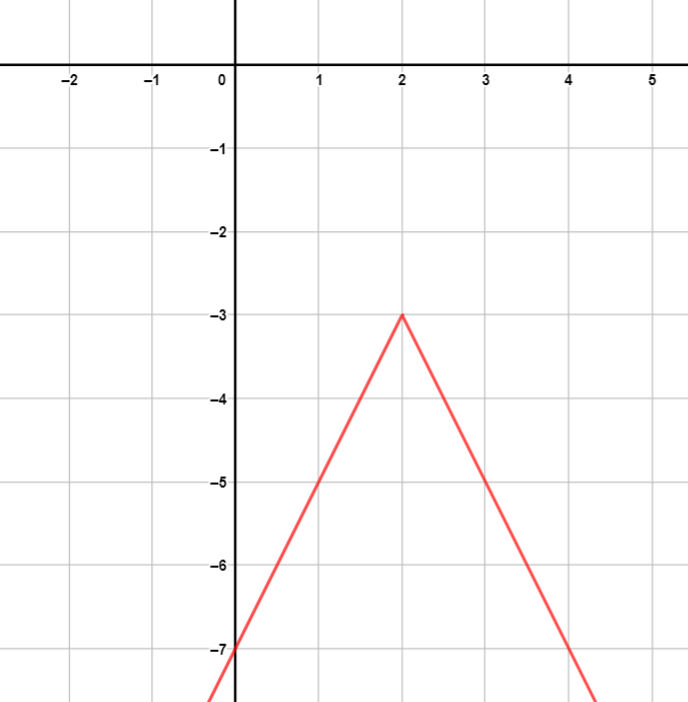 |
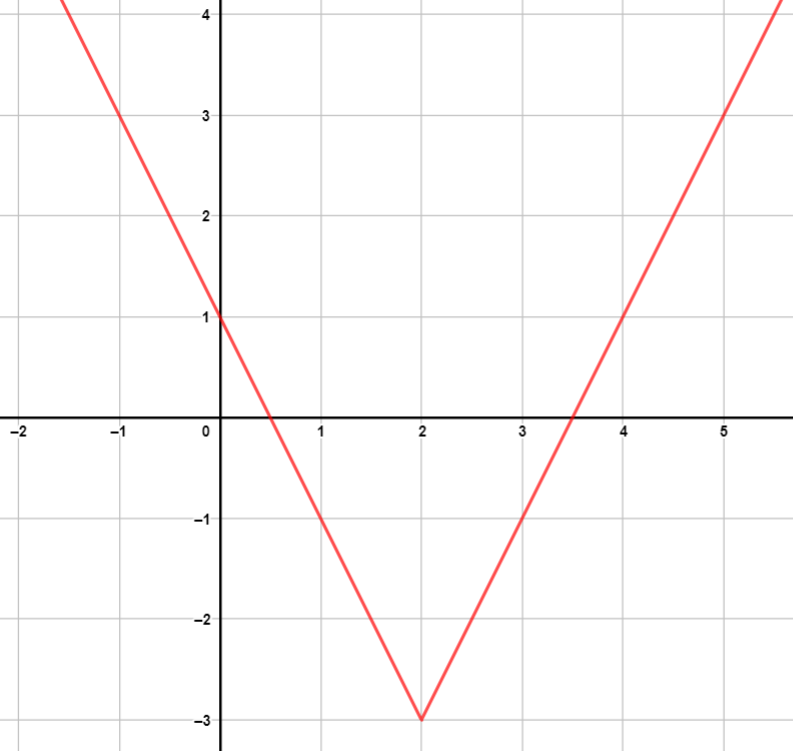 |
|
| المجال: ، المدى: | المجال: ، المدى: |
أكتب قاعدة اقتران القيمة المُطلقة الممثل بيانيًا في كل مما يأتي:
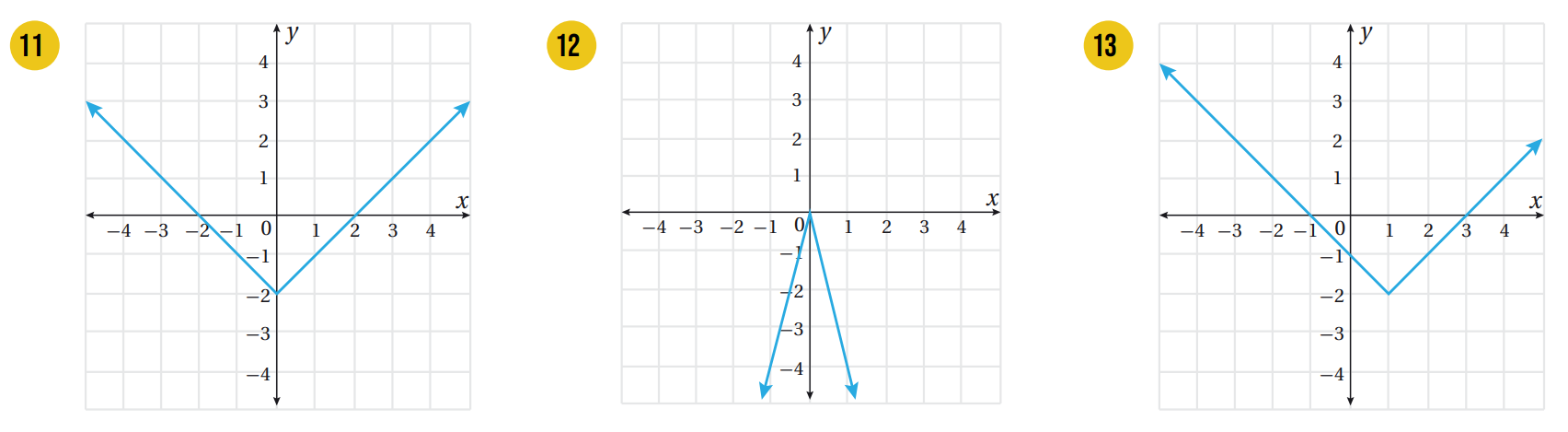 |
حلول أسئلة مهارات التفكير العُليا
14) تبرير : أيُّ الآتية تُمثل الاقتران ، مُبررًا إجابتي؟
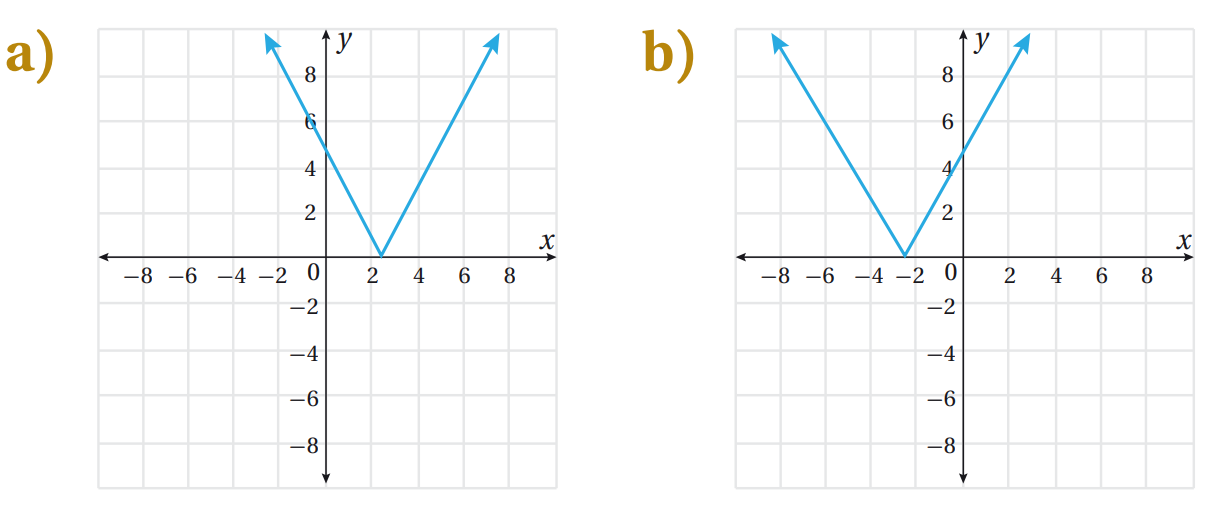
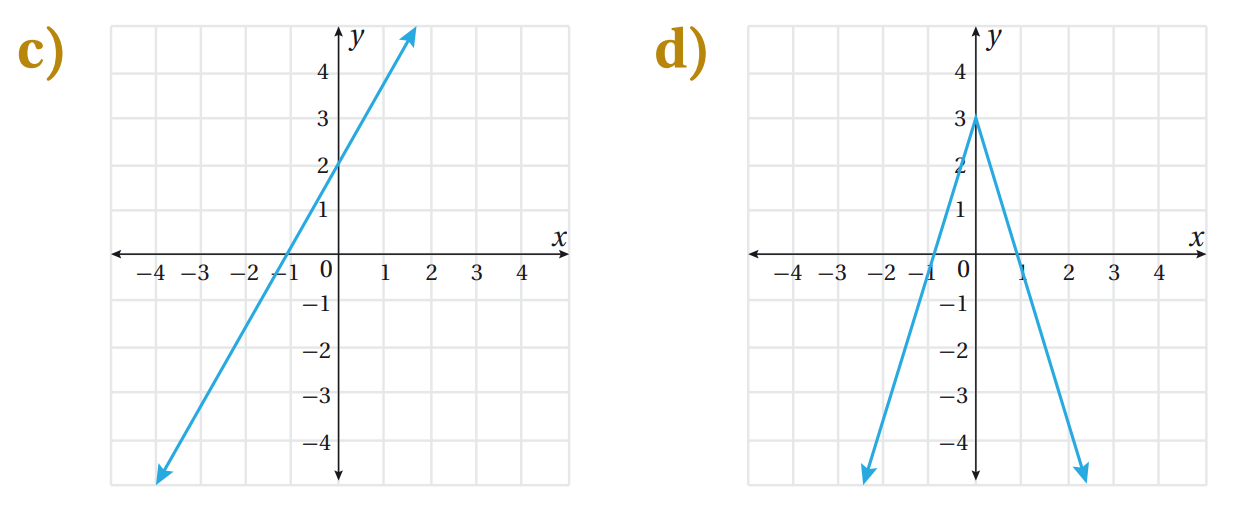
الحل:
بما أن a = 1 )عدد موجب) إذن منحنى الاقتران f(x) مفتوح للأعلى
رأس اقتران القيمة المطلقة
رأس الاقتران هو:
لذا : الخيار a هو التمثيل البياني للاقتران f(x).
15) مسألة مفتوحة: أكتب اقتران قيمة مطلقة ، مجاله مجموعة الأعداد الحقيقية ومداه (-∞ , 3].
الحل:
حلول أسئلة كتاب التمارين
إذا كان ، فأجيب على السؤالين الآتيين:
1) أعيد تعريف الاقترانf .
2) أجد كلًا من:
إذا كان : ، فأجيب على السؤالين الآتيين:
1) أعيد تعريف الاقترانf .
2) أجد كلًا من:
أمثل بيانيًا كل اقتران مما يأتي، محددًا مجله ومداه.
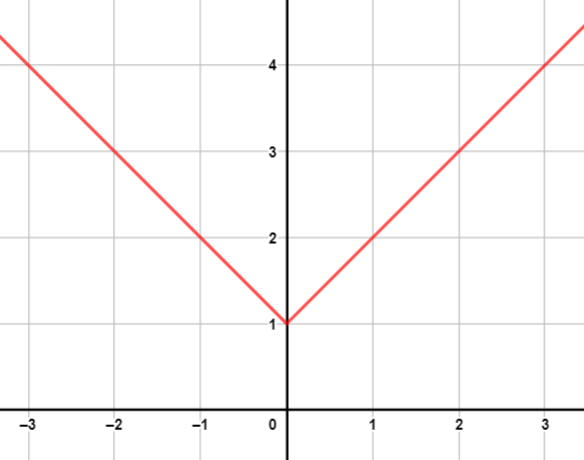 |
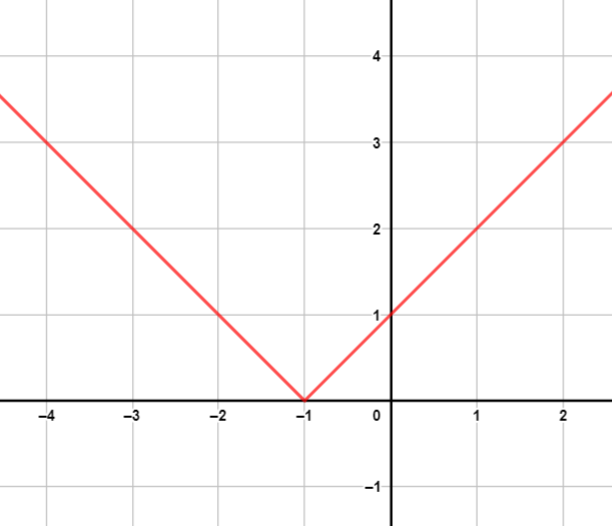 |
| المجال: ، المدى: | المجال: ، المدى: |
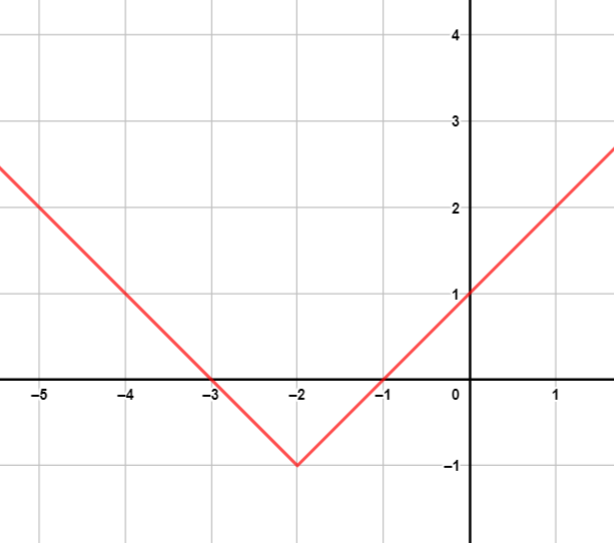 |
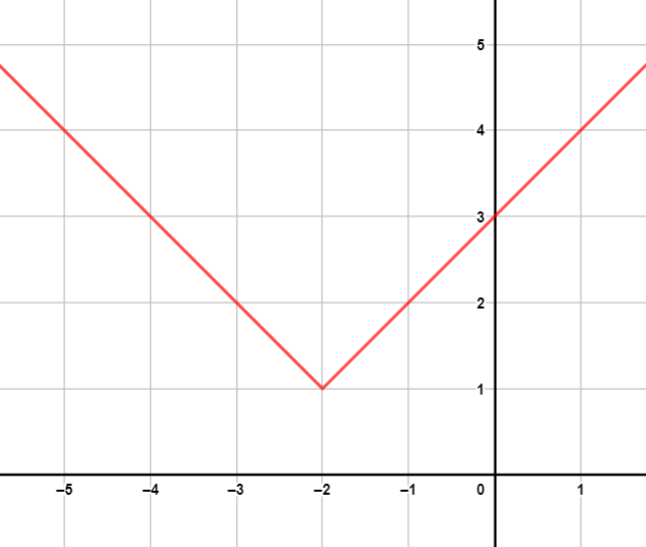 |
| المجال: ، المدى: | المجال: ، المدى: |
أكتب قاعدة اقتران القيمة المطلقة الممثل بيانيًا في كل مما يأتي:
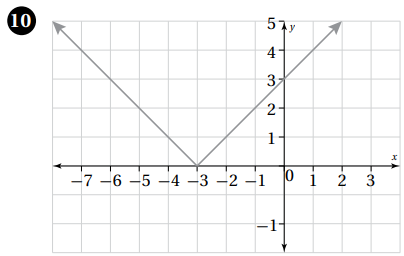 |
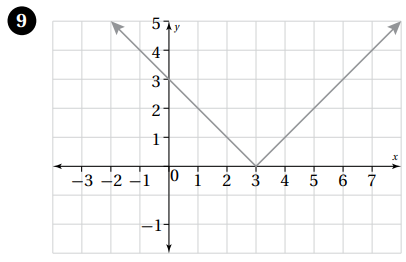 |
 |
 |