حلول أسئلة كتاب الطالب وكتاب التمارين
أتحقق من فهمي
أتحقق من فهمي صفحة 89 :
أحدد كل عدد من الأعداد الآتية إذا كان أوليا أم غير أولي :
|
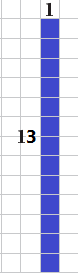
1) العدد 13 . الجواب :
العدد 13 أولي : لأنه أكبر من 1 وله عاملان فقط وهما 1 والعدد 13 نفسه . |
2) العدد 10 . الجواب :
العدد 10 غير أولي : لأن له أكثر من عاملين وهي : 10 , 5, 2, 1 . |
أتحقق من فهمي صفحة 90 :
أحدد العدد إذا كان أوليا أم غير أولي مما يأتي :
|
1) العدد 47 . الجواب : العدد 47 يقبل القسمة على 1 وعلى نفسه أيضا لكنه لا يقبل القسمة على أي عدد غيرهما . لذا فإن العدد 47 عدد أولي . |
2) العدد 85. الجواب : العدد 85 يقبل القسمة على 1 وعلى نفسه أيضا وهو يقبل القسمة على 5 لأن آحاد العدد 85 هي 5 لذا يوجد للعدد 85 أكثر من عاملين . إذن العدد 85 غير أولي . |
أتدرب وأحل المسائل
1) أحدد كل عدد من الأعداد الآتية إذا كان أوليا أم غير أولي :

الجواب :
|
الأعداد الأولية : 13, 29 , 37 , 59 لأن كل واحد منهم يقبل القسمة على نفسه وعلى 1 فقط .
|
الأعداد غير الأولية : 15 : لأنه يقبل القسمة على نفسه وعلى 1 ويقبل القسمة على 5 أيضا إذن له أكثر من عاملين . 22 : لأنه يقبل القسمة على نفسه وعلى 1 ويقبل القسمة على 2 أيضا . 48 : لأنه يقبل القسمة على نفسه وعلى 1 ويقبل القسمة على 2 . 75 : لأنه يقبل القسمة على نفسه وعلى 1 ويقبل القسمة على 5 . |
2) أكمل الجدول الآتي :
| العدد | عوامله | أولي أم غير أولي |
| 11 | 11 ,1 | أولي |
| 28 | 28 , 14, 7, 4, 2, 1 | غير أولي |
| 21 | 21, 7, 3, 1 | غير أولي |
| 36 | 36, 18, 12, 9, 6, 4, 3, 2, 1 | غير أولي |
3) بكم طريقة يمكنني ترتيب 13 طاولة مربعة على شكل مستطيل ؟ أبرر إجابتي .
الجواب :
بطريقة واحدة بحيث تكون 13 طاولة في صف واحد. (لأن العدد 13 عدد أولي).
4) أرادت تالا أن ترتب 25 لوحة على الحائط في صفوف متساوية , هل يمكنها أن تفعل ذلك ؟ أبرر إجابتي ؟
الجواب :
نعم تستطيع , بحيث تضع 25 لوحة في صف واحد أو أن تضع 5 لوحات في 5 صفوف .
مهارات التفكير
5) اكتشف المختلف : أحدد العدد المختلف عن الأعداد الأخرى وأفسر إجابتي .

الجواب :
العدد 51 عدد غير أولي لأن عوامله هي : 51 , 17, 3 , 1 أما بقية الأعداد فهي أعداد أولية تقبل القسمة على نفسها و 1 فقط .
6) تبرير : أضع كلمة ( صح ) أمام الجملة الصحيحة وكلمة ( خطأ) أمام الجملة غير الصحيحة في كل مما يأتي , وابرر إجابتي .
- الأعداد الفردية جميعها أعداد أولية. (خطأ).
فمثلا العدد 9 هو عدد فردي ولكنه ليس عددا أوليا لأن له أكثر من عاملين .
- لا يوجد عدد زوجي أولي. (خطأ).
فمثلا العدد 2 هو عدد زوجي وأولي لأن له عاملين فقط هما 2 و 1 .
- 1 , 2 , 3, 5 هي الأعداد الأولية الأربعة الأولية. (خطأ).
لأن العدد 1 لا يصنف ضمن الأعداد الأولية والأعداد غير الأولية فهو له عامل واحد فقط .
- العدد الأولي له عاملان فقط ( صح).
- 2 هو العدد الأولي الزوجي الوحيد ( صح).
لأن العدد 2 هو العدد الزوجي الوحيد الذي له عاملان فقط بينما بقية الأعداد الزوجية لها على الأقل 3 عوامل لأن كل عدد زوجي يقبل القسمة على 2 .
- لا يوجد عددان أوليان متتاليان ( خطـأ).
يوجد عددان أوليان متتاليان هما 2 , 3 .
7) تبرير : يقول سامي إن مجموع أي عددين أوليين يكون عددا زوجيا , هل هو على صواب ؟ أفسر إجابتي .
الجواب :
ليس على صواب , لأن العددين 2 و 3 أوليين لكن ناتج جمعهم هو 5 وهو عدد فردي .
8) تبرير : هل يوجد عدد أولي أكبر من 5 آحاده 5 , أبرر إجابتي .
الجواب :
لا يوجد , لأن الأعداد الأولية تقبل القسمة على نفسها وعلى 1 فقط , ولكن إذا كانت آحاد العدد 5 فهذا يعني أنه يقبل القسمة على 5 وهو ما يتنافى مع مفهوم العدد الأولي .
كتاب التمارين
1) أحدد كل عدد من الأعداد الآتية , إذا كان أوليا أم غير أولي :
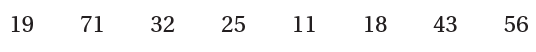
الجواب :
| الأعداد الأولية | الأعداد غير الأولية |
| 11 , 71 , 19, 43 | 18, 25, 32, 56 |
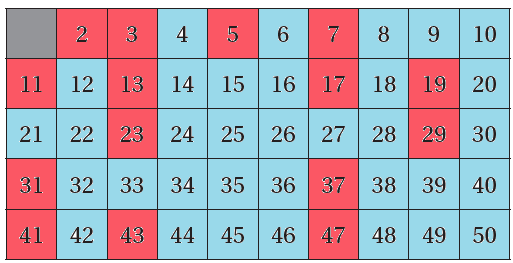
2) ألون الأعداد الأولية في لوحة المئة باللون الأحمر والأعداد غير الأولية باللون الأزرق .
3) أكتب الطرائق جميعها التي يمكن لنادر بها زراعة 37 نبتة فراولة في صفوف تحتوي على العدد نفسه من النباتات .
الجواب :
إما أن تكون في صف واحد أفقي وعددها 37 نبتة فراولة وإما أن تكون في صف عمودي وعددها 37 نبتة فراولة .
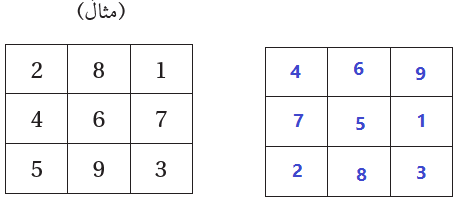
4) تحد : أرتب الأرقام من ( 1 إلى 9 ) في الشبكة أدناه بحيث يكون ناتج الجمع في كل صف وكل عمود عددا أوليا كما في المثال المعطى .
5) تفكير منطقي : الأعداد 13 , 17 أعداد أولية عند تغير ترتيب أرقام العددين ينتج 31 , 71 وهما عددان أوليان أيضا , هل إعادة ترتيب أرقام عدد أولي يعطي عددا أوليا دائما ؟
الجواب:
لا تصلح هذه العملية دائما على كل الأعداد فالعدد 41 عدد أولي فإذا بدلنا ترتيب المنازل يصبح 14 وهو عدد غير أولي .