رياضيات 7 فصل ثاني

حلول أسئلة أتحقق من فهمي 

5) احتمالَ سحبِ قطعةِ حلوى خضراءَ.

${\mathrm{P}}_{\left(\mathrm{خضراء}\right)}=\frac{3}{12}=\frac{1}{4}$                 عدد القطع الحمراء 3 والفضاء العيني للتجربة 12

6) احتمالَ سحبِ قطعةِ حلوى صفراءَ أَوْ خضراءَ.

${\mathrm{P}}_{\left(\mathrm{خضراءُ} \mathrm{أَوْ} \mathrm{صفراء}\right)}=\frac{5}{12}$            عدد القطع الصفراء 2 والخضراء 3 والفضاء العيني للتجربة 12

7) احتمالَ سحبِ قطعةِ حلوى ليسَتْ حمراءَ.

${\mathrm{P}}_{\left(\mathrm{حمراء} \mathrm{ليست}\right)}=\frac{7}{12}$                 عدد القطع الحمراء 5 أي أن القطع الاخرى 7 ليست حمراء والفضاء العيني للتجربة 12

8) احتمالَ سحبِ قطعةِ حلوى سوداءَ.

${\mathrm{P}}_{\left(\mathrm{سوداءٌ}\right)}=\frac{0}{12}$                        عدد القطع السوداء 0 والفضاء العيني للتجربة 12

 

3) إذا إذا كانَ احتمالُ خسارةِ الفريقِ المباراةَ 0.4 ، فَما احتمالُ أَلّأ يخسرَ الفريقُ المباراةَ؟ 

$$\begin{gathered} {\mathrm{P}}_{\left(\mathrm{الخسارة} \mathrm{عدم}\right)}=1-{\mathrm{P}}_{\left(\mathrm{الفريق} \mathrm{خسارة}\right)} \\ =1-0.4 \\ =0.6 \end{gathered}$$

4) إذا كانَ احتمالُ اختيارِ طالبةٍ مِنَ الصفِّ السابعِ ترتدي نظّارةً يساوي $\frac{\mathbf{1}}{\mathbf{9}}$فَما احتمالُ اختيارِ طالبةٍ لا ترتدي نظّارةً؟ 

$$\begin{gathered} {\mathrm{P}}_{\left(\mathrm{ترتدي} \mathrm{لا} \right)}=1-{\mathrm{P}}_{\left( \mathrm{نظارة} \mathrm{ترتدي}\right)} \\ =1-\frac{1}{9} \\ =\frac{8}{9} \end{gathered}$$

 

لدى أماني 32 بطاقةً مقسَّمةً كَما يأتي: (15 خضراءُ ، 18 مستطيلةٌ  5 حمراءُ مربعةٌ) أنظّمُ هذِهِ البياناتِ في جدولٍ ذي اتجاهَينِ.

يجب أن يظهر الجدول الوان البطاقات (خضراء أو حمراء) و شكلها (مستطيلة أو مربعة) 

الخطوة 1: ننظم جدولاً ونضيف اليه صفأً وعموداً لكتابة المجموع ، ونضيف المعلومات الواردة في المسألة 

المجموع	مستطيلة	مربعة
15			خضراء
		5	حمراء
32	18		المجموع

الخطوة 2: استعمل المجموعَ الكلّيَّ للبطاقات لَِأجِدَ القِيَمَ المجهولةَ. 

المجموع	مستطيلة	مربعة
15	6	9	خضراء
17	12	5	حمراء
32	18	14	المجموع

 

4) إذا اختيرَ طفلٌ عشوائيًّا، فَما احتمالُ أنْ تكونَ بنتًا تفضلُ اللونَ الأخضرَ؟

$$\begin{gathered} {\mathrm{P}}_{\left({\mathrm{الأخضر} \mathrm{تفضل}}^{}\mathrm{بنت}\right)}=\frac{{\mathrm{الأخضر} \mathrm{تفضل}}^{}\text{بنت}}{{\mathrm{الكلي}}^{}\mathrm{الاطفال} \mathrm{عدد}} \\ = \frac{8}{60} \end{gathered}$$

5) إذا اختيرَ طفلٌ عشوائيًّا، فَما احتمالُ أنْ يكونَ طفلً يفضلُ اللونَ الأحمرَ؟

$$\begin{gathered} {\mathrm{P}}_{\left({\mathrm{الأحمر} \mathrm{يفضل}}^{}\mathrm{طفل}\right)}=\frac{ \mathrm{الأحمر}{\mathrm{يفضل}}^{}\text{طفل}}{{\mathrm{الكلي}}^{}\mathrm{الاطفال} \mathrm{عدد}} \\ = \frac{16+8}{60} \\ =\frac{24}{60} \end{gathered}$$

6) إذا اختيرَ طفلٌ عشوائيًّا، فَما احتمالُ ألّأ تكونَ بنتًا؟

$$\begin{gathered} {\mathrm{P}}_{\left( \mathrm{بنتاً} \mathrm{لاتكون} \right)}=\frac{ \mathrm{الاولاد} \mathrm{الاطفال} \mathrm{عدد}}{{\mathrm{الكلي}}^{}\mathrm{الاطفال} \mathrm{عدد}} \\ =\frac{12+8+8}{60} \\ = \frac{28}{60} \\ = \frac{7}{15} \end{gathered}$$

---

---

حلول أسئلة أتدرب وأحل المسائل 

أيُّ التجاربِ العشوائيةِ الآتيةِ نواتجُها متساويةُ الاحتمالِ؟

1) تدويرُ مؤشرِ القرصِ المجاورِ. 

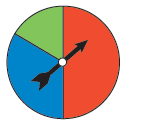
النواتج ليست متساوية الاحتمال لأن فرص ظهور الألوان مختلفةً،

2) اختيارُ كرةٍ زجاجيةٍ مِنْ وعاءٍ يحتوي على 5 كراتٍ حمراءَ وَ 5 كراتٍ خضراءَ.

النواتج متساوية الاحتمال لأن لِكلِّ كرة فرصةُ الظهورِ نفسُها

 

3) إذا كانَ احتمالُ فوزِ فريقِ كرةِ القدمِ الّذي تشجعُهُ ناديا يساوي $\frac{\mathbf{3}}{\mathbf{7}}$فَما احتمالُ أَلّا يفوزَ الفريقُ؟

$$\begin{gathered} {\mathrm{P}}_{\left(\mathrm{الفوز} \mathrm{عدم} \right)}=1-{\mathrm{P}}_{\left( \mathrm{الفوز}\right)} \\ =1-\frac{3}{7} \\ =\frac{4}{7} \end{gathered}$$

4)  إذا كانَ احتمالُ أنَ تصلَ الحافلةُ في موعدِها يساوي $\frac{\mathbf{8}}{\mathbf{11}}$فَما احتمالُ أَنْ تتأخرَ الحافلةُ

$$\begin{gathered} {\mathrm{P}}_{\left( \mathrm{التأخر} \right)}=1-{\mathrm{P}}_{\left( \mathrm{الموعد} \mathrm{في} \right)} \\ =1-\frac{8}{11} \\ =\frac{3}{11} \end{gathered}$$

 

أدارَ فادي مؤشرَ القرصِ المجاورِ، أَجِدُ احتمالَ أَنْ يقفَ المؤشرُ عندَ:

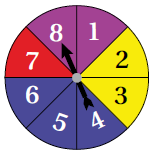
5) قطاعٍ أزرقَ.

${\mathrm{P}}_{\left(\mathrm{أزرق} \mathrm{قطاع}\right)}=\frac{3}{8}$      

6) قطاعٍ يحملُ رقْمًا سالبًا.

${\mathrm{P}}_{\left( \mathrm{سالب} \mathrm{رقم}\right)}=\frac{0}{8}$ 

7) قطاعٍ لونُهُ ليسَ أحمرَ.

$$\begin{gathered} {\mathrm{P}}_{\left(\mathrm{أحمر} \mathrm{ليس}\right)}=1-{\mathrm{P}}_{\left(\mathrm{أحمر} \mathrm{لونه}\right)} \\ =1-\frac{1}{8} \\ =\frac{7}{8} \end{gathered}$$

8) قطاعٍ أصفرَ يحملُ رقْمًا زوجيًّا.

${\mathrm{P}}_{\left(\mathrm{زوجي} \mathrm{أصفر}\right)}=\frac{1}{8}$

9) قطاعٍ يحملُ رقْمًا أكبرَ مِنْ 3

${\mathrm{P}}_{\left(3\mathrm{من} \mathrm{أكبر} \right)}=\frac{5}{8}$

10) قطاعٍ يحملُ رقْمًا أقلَّ مِنْ 10

${\mathrm{P}}_{\left(10\mathrm{من} \mathrm{أقل}\right)}=\frac{8}{8}$

11) قطاعٍ أصفرَ أَوْ يحملُ رقْمًا أكبرَ مِنْ 3

${\mathrm{P}}_{\left(3<\mathrm{أو} \mathrm{أصفر}\right)}=\frac{2+5}{8}=\frac{7}{8}$

 

أكملُ الجدولَ الآتيَ الّذي يُظهرُ أعدادَ الأقراصِ الملونةِ المجاورةِ لَهُ وَألوانَها:

أصفر  وردي أزرق   2 0 4 A 2 2 1 B 2 1 3 C 0 3 0 D

 

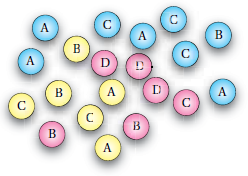إذا اختيرَ قرصٌ واحدٌ عشوائيًّا مِنْ مجموعةِ الأقراصِ في السؤالِ السابقِ، فَأَجِدُ:

12) احتمالَ اختيارِ حرفِ A مكتوبًا على قرصٍ أصفرَ. 

${\mathrm{P}}_{\left( \mathrm{اصفر} \mathrm{على} \mathrm{A} \right)}=\frac{2}{20}$

13) احتمالَ اختيارِ قرصٍ أزرقَ.

${\mathrm{P}}_{\left( \mathrm{ازرق} \right)}=\frac{8}{20}$

14) احتمالَ اختيارِ قرصٍ مكتوبٍ عَلَيْهِ الحرفُ C

${\mathrm{P}}_{\left( \mathrm{C} \mathrm{حرف} \right)}=\frac{6}{20}$

 

اختيرَ 38 شخصًا مِنْ محافظتَيِ الزرقاءِ وَالعقبةِ لِلمشاركةِ في دراسةٍ طبّيةٍ، وَكانَ توزيعُهُمْ كَما يأتي، أنظّمُ هذِهِ البياناتِ في جدولٍ ذي اتجاهَينِ، ثمَّ أستعملُهُ لِلإجابةِ عَنِ الأسئلةِ الآتيةِ:

"18 شخصًا مِنْ محافظةِ الزرقاءِ مِنْهُمْ 7 رجالٍ و 8 نساءٍ مِنْ محافظةِ العقبةِ."

أنظم الجدول مستعيناً بالمعلومات الواردة في السؤال 

المجموع	الزرقاء	العقبة
19	7	12	رجال
19	11	8	نساء
38	18	20	المجموع

15) ما عددُ الأشخاصِ الّذين شاركوا في الدراسةِ مِنْ محافظةِ العقبةِ؟

20 شخص 

16) ما عددُ الرجالِ الّذين شاركوا في الدراسةِ؟

19 شخص 

17) ما عددُ الرجالِ الّذين شاركوا في الدراسةِ مِنْ محافظةِ العقبةِ؟

12 شخص 

 

تبريرٌ: يبيّنُ الجدولُ المجاورُ عددَ قطعِ الحلوى المغلَّفةِ وَغيرِ المغلَّفةِ الّتي اشترَتْها فدوى، وَهِيَ بِثلاثِ نكهاتٍ مختلفةٍ، إذا اختارَتْ فدوى قطعةَ حلوى عشوائيًّا، فَأُكملُ الجملَ الآتيةَ بِما يناسبُها مبررًا إجابتي:

شوكولاتة	فراولة	برتقال
2	4	3	مغلفة
5	3	8	غير مغلفة

18) احتمالُ أنْ تكونَ قطعةُ الحلوى الّتي اختيرَتْ مغلفةً وَبِنكهةِ البرتقالِ يساوي

${\mathrm{P}}_{\left(\mathrm{البرتقال} \mathrm{بنكهة} \mathrm{مغلفة}\right)}=\frac{3}{25}$

19) احتمالُ أنْ تكونَ قطعةُ الحلوى الّتي اختيرَتْ غيرَ مغلفةٍ وَبنكهةِ الشوكولاته يساوي

${\mathrm{P}}_{\left(\mathrm{الشوكولاتة} \mathrm{بنكهة} \mathrm{مغلفة} \mathrm{غير} \right)}=\frac{5}{25}$

20) احتمالُ أنْ تكونَ قطعةُ الحلوى الّتي اختيرَتْ بِنكهةِ الفراوِلةِ يساوي ${\mathrm{P}}_{\left(\mathrm{الفراولة} \mathrm{بنكهة} \right)}=\frac{7}{25}$

21)مغلفة وبنكهة الفراولة يساوي 16%

22) مغلفة  بنكهة الفراولة أو غير مغلفة وبنكهة البرتقال يساوي 48%

 

23) أكتبُُ ما الفرقُ بينَ الحادثِ وَاحتمالِ الحادثِ؟

الحادث: هو ناتج واحد أو أكثر من نواتج التجربة العشوائية

احتمال وقوع الحادث: هو فرصة وقوع الحادث و يساوي نسبةَ عددِ عناصرِ الحادثِ إلى عددِ النواتجِ الممكنةِ جميعِها(الفضاءُ العينِيُّ).

---

---

حلول أسئلة كتاب التمارين 

اختارَتْ ناديا بطاقةً عشوائيًّا مِنْ بينِ البطاقاتِ المجاورةِ، أجِدُ احتمالَ اختيارِ:

1) بطاقةٍ تحملُ دائرةً.

${\mathrm{P}}_{\left(\mathrm{دائرة} \mathrm{تحمل} \mathrm{بطاقة}\right)}=\frac{3}{12}$

2) بطاقةٍ تحملُ مستطيلً وَالعددَ 3

${\mathrm{P}}_{\left(3 \mathrm{والعدد} \mathrm{مستطيل} \mathrm{تحمل} \mathrm{بطاقة}\right)}=\frac{2}{12}$

3) بطاقةٍ تحملُ العددَ 1

${\mathrm{P}}_{\left( 1\mathrm{العدد} \mathrm{تحمل} \mathrm{بطاقة}\right)}=\frac{3}{12}$

4) بطاقةٍ تحملُ شكلاً لَهُ أضلاعٌ.

${\mathrm{P}}_{\left(\mathrm{اضلاع} \mathrm{له} \mathrm{شكل} \mathrm{تحمل} \mathrm{بطاقة}\right)}=\frac{9}{12}$

 

يبيّنُ الشكلُ المجاورُ 10 كُراتٍ مرقَّمةً بِالأرقامِ 1 وَ 2 وَ 3 وَ 4 أكملُ ترقيمَ الكراتِ إذا علمْتُ أَنَّهُ عندَ اختيارِ كُرةٍ عشوائيًّا فَإِنَّ:

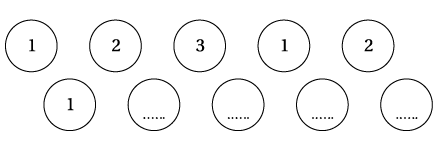
•فرصةَ ظهورِ الرقْمِ 4 مساويةٌ لِفرصةِ ظهورِ الرقْمِ 3 

أي أن الكرات التي تحمل الرقم 4 = الكرات التي تحمل الرقم 3

•فرصةَ ظهورِ الرقْمِ 1 هِيَ الأعلى بينَ الأرقامِ.

الكرات تحمل رقم 1 هي الأكثر 

 

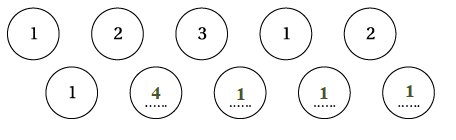
اختارَتْ نسرينُ عشوائيًّا بطاقةً مِنْ بينِ البطاقاتِ المجاورةِ. أضعُ إشارةً على مقياسِ الاحتمالِ لِتدلَّ على احتمالِ وقوعِ الحوادثِ الآتيةِ:

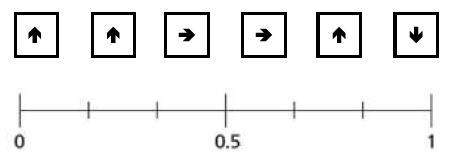
5) A: بطاقةٌ تحملُ سهمًا. 

${\text{P}}_{\left(\mathrm{سهم} \mathrm{تحمل}\right)}\text{=}\frac{6}{6}\text{=1}$

6) B:بطاقةٌ تحملُ سهمًا متجهًا لِلأسفلِ $\downarrow$

${\text{P}}_{\left(\downarrow \mathrm{سهم} \mathrm{تحمل}\right)}\text{=}\frac{1}{6}$

7) B: بطاقةٌ تحملُ سهمًا متجهًا لِلأعلى $\uparrow$

${\text{P}}_{\left(\uparrow \mathrm{سهم} \mathrm{تحمل}\right)}\text{=}\frac{3}{6}\text{=0.5}$

8) D: بطاقةٌ تحملُ سهمًا متجهًا لِليسارِ $\leftarrow$

${\text{P}}_{\left(\leftarrow \mathrm{سهم} \mathrm{تحمل}\right)}\text{=}\frac{0}{6}\text{=0}$

التمثيل على مقياس الإحتمال 

 

يبيّنُ الجدولُ المجاورُ ألوانَ المركباتِ في موقفٍ لِلسيّاراتِ، إذا اختيرَتْ مركبةٌ عشوائيًّا، أَجِدُ احتمالَ:

شاحنةٌ	سيّارةٌ
2	7	أحمرُ
7	3	أبيضُ
0	11	أسودُ
1	4	أزرقُ

9) اختيارِ شاحنةٍ.

${\mathrm{P}}_{\left(\mathrm{شاحنة} \mathrm{اختيار}\right)}=\frac{10}{35}$

10) اختيارِ سيّارةٍ زرقاءَ.

${\mathrm{P}}_{\left(\mathrm{زرقاء} \mathrm{سيارة}\right)}=\frac{4}{35}$

11) اختيارِ شاحنةٍ سوداءَ أَوْ سيّارةٍ.

${\mathrm{P}}_{\left(\mathrm{شاحنة} \mathrm{او} \mathrm{سيارة}\right)}=\frac{25}{35}$