الرياضيات فصل أول

كتاب التمارين صفحة 6:

قبل دراسة وحدة الاقترانات الأسية واللوغاريتمية، على الطالب التأكد من إتقانه لمهارات أساسية قد تعلمها في صفوف سابقة مثل:

1. تبسيط المقادير الأسية

2. حل المعادلات الأسية

3. إيجاد الاقتران العكسي

---

أولًا: تبسيط المقادير الأسية:

لتبسيط المقادير الأسية يتم استخدام قوانين الأسس التي تعلمناها سابقًا.

حيث لأي عددين حقيقين a,b وعددين صحيحين n,m فإنّ:

- تنطبق خصائص ضرب القوى وقسمتها على الأسس النسبية كذلك.

 

- تكون العبارة الأسية في أبسط صورة إذا:

1) ظهر الأساس مرة واحدة، وكانت الأسس جميعها موجبة

2) لم تتضمن العبارة قوة القوى

3) كانت الكسور والجذور جميعها في أبسط صورة.

 

1) جد ناتج كل مما يأتي بأبسط صورة:

 

                   $a) {\left(625\right)}^{\frac{3}{4}} b) \sqrt[4]{81 a^{12}} c) \frac{64 a^{7 } b^6}{48 a^2 b^{-5}}$        

الحل:

 $a) {\left(625\right)}^{\frac{3}{4}}$

${\left(625\right)}^{\frac{3}{4}} = {\left(\sqrt[4]{625}\right)}^3$	الصورة الأسية للجذر
$= {\left(5\right)}^3$	$\sqrt[4]{625}=\sqrt[4]{5^4}=5$
$=125$	$5^3=5\times 5\times 5=125$

 

 

$b) \sqrt[4]{81 a^{12}}$

$\sqrt[4]{81 a^{12}} =\sqrt[4]{81} \sqrt[4]{a^{12}}$	خصائص الجذور
$=\sqrt[4]{81} a^{\frac{12}{4}}$	الصورة الأسية للجذر
$= 3 a^3$	بالتبسيط: $\sqrt[4]{81}=\sqrt[4]{3^4}=3$

 

 $c) \frac{64 a^7 b^6}{48 a^2 b^{-5}}$

$\frac{64 a^7 b^6}{48 a^2 b^{-5}} = \frac{64}{48} \times \frac{a^7}{a^2}\times \frac{b^6}{b^{-5}}$	خصائص الكسور
$= \frac{64}{48}( a^{7-2}) \left(b^{6--5}\right)$	خصائص الأسس
$=\frac{4}{3} a^5 b^{11}$	بالتبسيط

---

ثانيًا: حل المعادلات الأسية:

1) تعريفها: المعادلة الأسية هي عبارة رياضية أساسها عددًا حقيقيًا والأس متغير وتحتوي إشارة المساواة.

 

2) حل المعادلة الأسية: عند حل المعادلة الأسية عليك:

        - كتابة طرفي المعادلة بصورة أسية وبدلالة الأساس نفسه.

        - تبسيط المعادلة مستعملًا قوانين الأسس.

        - حل المعادلة بمساواة الأساسات.

 

3)  جد حل كل من المعادلات الأسية الآتية:

                                                   $a) 2^{x+3}=128 b) {\left(\frac{1}{9}\right)}^x=729 c) 3^{-x}=\frac{1}{243}$            

الحل:

$a) 2^{x+3}=128$ 

$2^{x+3}=128$	المعادلة الأصلية
$2^{x+3}=2^7$	بكتابة العدد 128 بالصورة الأسية
$x+3 = 7$	بمساواة الأسس
$x = 4$	بحل المعادلة الخطية

 

 $b) {\left(\frac{1}{9}\right)}^x=729$

${\left(\frac{1}{9}\right)}^x=729$	المعادلة الأصلية
${\left(\frac{1}{9}\right)}^x=9^3$	بكتابة العدد 729 بالصورة الأسية
$9^{-x}= 9^3$	بكتابة طرفي المعادلة بدلالة الأساس نفسه مستخدمًا قوانين الأسس (قاعدة الأس السالب)
$-x=3\to x=-3$	بما أن الأساسات متساوية فإن الأسس متساوية

 

 $c) 3^{-x}=\frac{1}{243}$

$3^{-x}=\frac{1}{243}$	المعادلة الأصلية
$3^{-x}=\frac{1}{3^5}$	بكتابة العدد 243 بالصورة الأسية
$3^{-x}=3^{-5}$	بكتابة طرفي المعادلة بدلالة الأساس نفسه مستخدمًا قوانين الأسس
$-x=-5 \to x=5$	بما أن الأساسات متساوية فإن الأسس متساوية

 

---

ثالثًا: الاقتران العكسي للاقترانات:

 

 الاقتران: هو علاقة تربط كل عنصر في المجال بعنصر واحد فقط في المدى.

    - بما أن كل اقتران هو علاقة فإنه يمكن إيجاد علاقة عكسية للاقتران (معكوس للاقتران)

   - يرمز إلى الاقتران العكسي للاقتران $f\left(x\right)$ بالرمز $f^{-1}\left(x\right)$ ويُقرأ معكوس الاقتران $f\left(x\right)$

 

يمكن تحديد إذا كان معكوس الاقتران يمثل اقترانًا أم لا بــ:

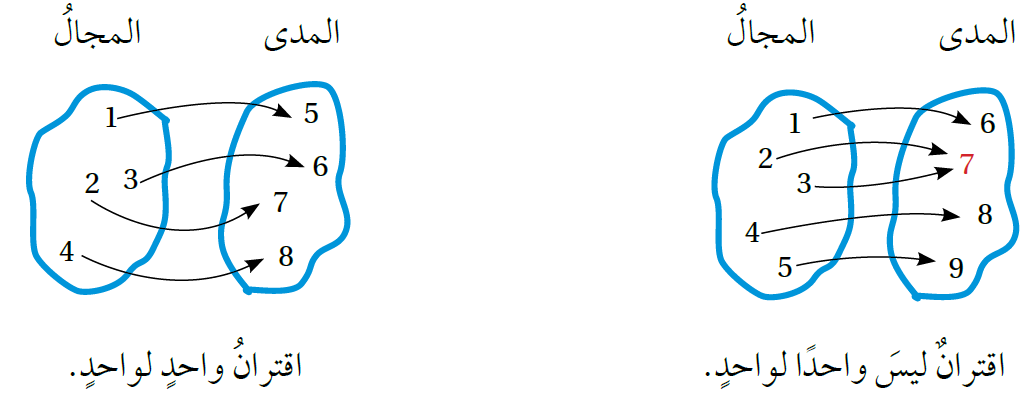
1) النظر إلى $f\left(x\right)$ نفسه؛ فإذا ارتبط كل عنصر في المدى بعنصر واحد فقط في المجال كان المعكوس اقترانًا وسُمي الاقتران $f\left(x\right)$اقترانًا  واحدًا لواحد.

 

 

 

 

 

 

 

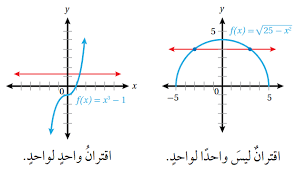
2) باستعمال طريقة اختبار الخط الأفقي ؛ وذلك برسم أي خط أفقي للتأكد أنه لا يقطع منحنى $f\left(x\right)$ في أكثر من نقطة.

 

يمكن إيجاد الاقتران العكسي باتباع الخطوات الآتية:

      1) كتابة الاقتران بصورة $y=f\left(x\right)$

      2) إعادة ترتيب المعادلة بجعل x موضوع القانون

     3) تغيير الرمز x  إلى y ، والرمز y إلى  x بالصيغة الناتجة بالخطوة السابقة.

     4) كتابة $f^{-1}\left(x\right)$ مكان y لينتج قاعدة الاقتران العكسي $f^{-1}\left(x\right)$

 

 

1) جد الاقتران العكسي لكل اقتران مما يأتي:

 $a) f(x)=x+8 b)f\left(x\right)=\frac{x}{5}+2 c) f\left(x\right)=6x^3$           

 

 

الحل:

$a) f(x)=x+8$ 

$y=x+8$	اكتب الاقتران بصورة $y=f\left(x\right)$
$x=y-8$	أعد ترتيب المعادلة بجعل x في طرف لوحدها
$y=x-8$	غير الرمز  x بـــ y وَ y بـــ x  في الصيغة السابقة
$f^{-1}\left(x\right)=x-8$	اكتب $f^{-1}\left(x\right)$ مكان y لتنتج قاعدة الاقتران العكسي $f^{-1}\left(x\right)$

 

 

$b) f(x)=\frac{x}{5}+2$

$y=\frac{x}{5}+2$	اكتب الاقتران بصورة$y=f\left(x\right)$
$y-2=\frac{x}{5}$$5(y-2)=x$ $5y-10=x$ $x=5y-10$	أعد ترتيب المعادلة بجعل x في طرف لوحدها
$y=5x-10$	غير الرمز  x بـــ y وَ y بـــ x  في الصيغة السابقة
$f^{-1}\left(x\right)=5x-10$	اكتب $f^{-1}\left(x\right)$ مكان y لينتج قاعدة الاقتران العكسي $f^{-1}\left(x\right)$

 

 $c) f(x)=6x^3$

$y=6x^3$	اكتب الاقتران بصورة$y=f\left(x\right)$
$$\begin{gathered} \frac{y}{6}=x^3 \\ \sqrt[3]{\frac{y}{6}}=x \end{gathered}$$	أعد ترتيب المعادلة بجعل x في طرف لوحدها
$y=\sqrt[3]{\frac{x}{6}}$	غير الر مز  x بـــ y وَ y بـــ x  في الصيغة السابقة
$f^{-1}\left(x\right)=\sqrt[3]{\frac{x}{6}}$	اكتب $f^{-1}\left(x\right)$ مكان y لينتج قاعدة الاقتران العكسي $f^{-1}\left(x\right)$