التشابه

مَفاهِيمُ أَساسِيَّةٌ :

يكونُ الشكلانِ متشابهَينِ إذا كانَ لَهُما الشكلُ نفسُهُ، وَليسَ بِالضرورةِ أنْ يكونَ لَهُما المقاسُ نفسُهُ. وَيُستخدَمُ الرّمزُ (~) لِلدلالةِ على أنَّ الشكلَينِ متشابهانِ.

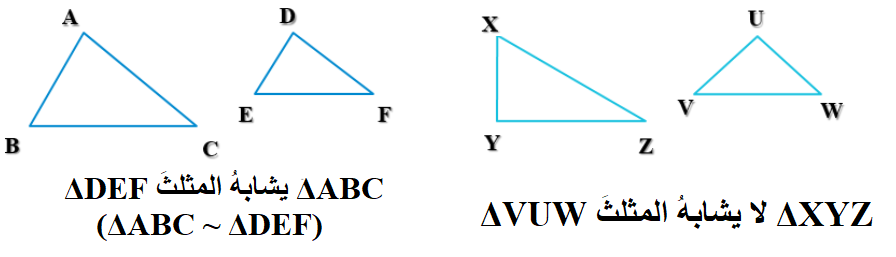
المضلعات المتشابهة :مضلعاتٌ زواياها المتناظرةُ متطابقةٌ، وَأطوالُ أضلاعِها المتناظرةِ متناسبةٌ.

إذا تشابهَ مضلعانِ فَإنَّ زواياهُما المتناظرةَ متطابقةٌ ،وَأطوالَ أضلاعِهِما المتناظرةِ متناسبةٌ.

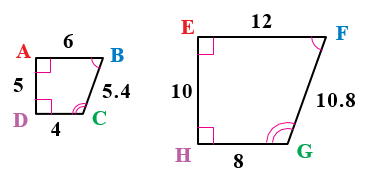
بِالرّموزِ إذا كانَ ABCD ~ EFGH  

∠A ≅ ∠E , ∠B ≅ ∠F , ∠C ≅ ∠G , ∠D ≅ ∠H : الزوايا المتطابقةَ

 وَالنسبةَ بينَ أطوالِ الأضلاعِ المتناظرةِ متساويةٌ $\frac{EF}{AB}=\frac{FG}{BC}=\frac{GH}{CD}=\frac{HE}{DA}=\frac{2}{1}$

مثال 1: في الشكلِ المجاورِ ΔRST ~ ΔXYZ 

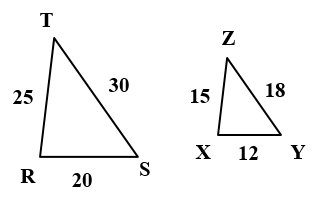
1)أكتبُ أزواجَ الزوايا المتناظرةِ:

∠R ≅ ∠X , ∠S ≅ ∠Y , ∠T ≅ ∠Z

2)أَجِدُ النسبةَ بينَ طولَيْ كُلِّ ضلعَينِ متناظِرَينِ بِأبسطِ صورةٍ، ثمَّ أكتبُ جملةَ التناسُبِ: 

$$\begin{gathered} \frac{\mathrm{RS}}{\mathrm{XY}}=\frac{20}{12}=\frac{5}{3} \\ \frac{\mathrm{ST}}{\mathrm{YZ}}=\frac{30}{18}=\frac{5}{3} \\ \frac{\mathrm{TR}}{\mathrm{ZX}}=\frac{25}{15}=\frac{5}{3} \end{gathered}$$

إذنْ، جملةُ التناسُبِ هِيَ $\frac{\mathrm{RS}}{\mathrm{XY}}=\frac{\mathrm{ST}}{\mathrm{YZ}}=\frac{\mathrm{TR}}{\mathrm{ZX}}$

 

تُسمّى النسبةُ بينَ طولَيِ الضلعَينِ المتناظِرَينِ في المضلعَينِ المتشابهَينِ عاملَ المقياسِ.

مثال 2: أبيّنُ ما إذا كانَ المثلثانِ المجاورانِ متشابهَينِ، ثمَّ أَجِدُ عاملَ المقياسِ:

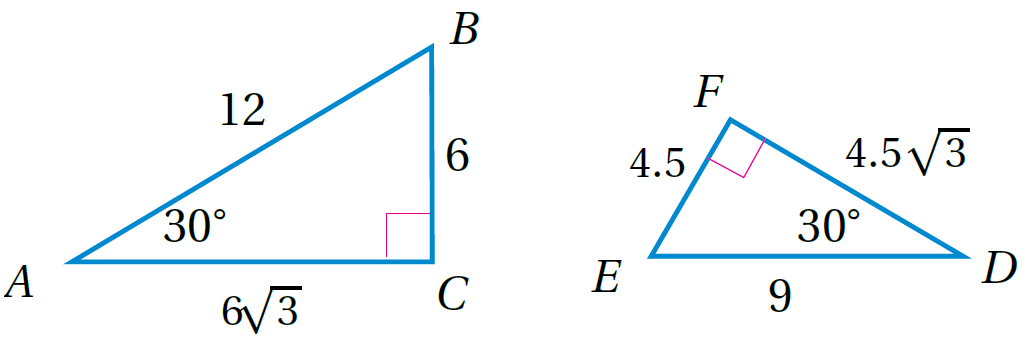
الْخُطْوَةُ 1: أَجِدُ قياسَ الزاويةِ الثالثةِ في كلٍّ مِنَ المثلثَينِ:

 $\mathrm{m}\angle \mathrm{A} + \mathrm{m}\angle \mathrm{B} + \mathrm{m}\angle \mathrm{C} ={180}^{°}$               مجموع قياس زوايا المثلث = 180 درجة

$$\begin{gathered} {30}^{°}+m\angle B+{90}^{°}={180}^{°} \\ m\angle B+{120}^{°}={180}^{°} \\ m\angle B={60}^{°} \end{gathered}$$                           وبتعويض قياس الزوايا A,C نجد قياس الزاوية B

يساوي ° 60 ∠B إذنْ، قياسُ

 

               مجموع قياس زوايا المثلث = 180 درجة               $\mathrm{m}\angle \mathrm{D} + \mathrm{m}\angle \mathrm{E} + \mathrm{m}\angle \mathrm{F} ={180}^{°}$

 $$\begin{gathered} {30}^{°}+\mathrm{m}\angle \mathrm{E}+{90}^{°}={180}^{°} \\ \mathrm{m}\angle \mathrm{B}+{120}^{°}={180}^{°} \\ \mathrm{m}\angle \mathrm{E}={60}^{°} \end{gathered}$$                             وبتعويض قياس الزوايا D,F نجد قياس الزاوية E

يساوي ° 60 ∠E إذنْ، قياسُ
∠B ≅ ∠E , ∠A ≅ ∠D , ∠C ≅ ∠F وَمِنْهُ
إذنْ، الزوايا المتناظرةُ متطابقةٌ

 

الْخُطْوَةُ 2:أَجِدُ النسبةَ بينَ طولَيْ كُلِّ ضلعَينِ متناظِرَينِ:

$$\begin{gathered} \frac{\mathrm{AB}}{\mathrm{DE}}=\frac{12}{9}=\frac{4}{3} \\ \frac{\mathrm{AC}}{\mathrm{DF}}=\frac{6\sqrt{3}}{4.5\sqrt{3}}=\frac{4}{3} \\ \frac{\mathrm{BC}}{\mathrm{EF}}=\frac{6}{4.5}=\frac{4}{3} \end{gathered}$$

النِّسبُ متساويةٌ، إذنْ، أطوالُ الأضلاعِ المتناظرةِ متناسبةٌ. 

بِما أنَّ الزوايا المتناظرةَ متطابقةٌ، وَأطوالَ الأضلاعِ المتناظرةِ متناسبةٌ، إذنْΔABC ~ ΔDEF وَعاملُ المقياسِ يساوي $\frac{4}{3}$

 

يمكنُ استعمالُ خواصِّ المضلَّعاتِ المتشابهةِ في إيجادِ القياساتِ المجهولةِ.

مثال3:  في الشكلِ المجاورِ ΔDEF ~ ΔMNP أَجِدُ قيمةَ المتغيِّرِ  x 

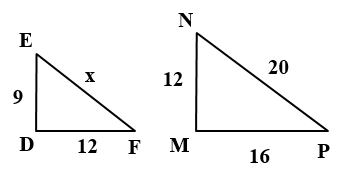
$\frac{\mathrm{MP}}{\mathrm{DF}}=\frac{\mathrm{NP}}{\mathrm{EF}}$                                          نكتب تناسباً ونعوض القيم لايجاد المتغير  x

$$\begin{gathered} \frac{16}{12}=\frac{20}{\mathrm{x}} \\ 16\mathrm{x}=240 \\ \mathrm{x}=15 \end{gathered}$$                                             بالضرب التبادلي بعد تعويض القيم x=15

 

.ايضًا k فَإِنَّ النسبةَ بينَ محيطَيهِما تساوي ،k إذا تشابهَ مضلّعانِ وَكانَ عاملُ المقياسِ لَهُما يساوي

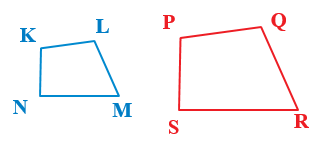
إذا تشابهَ مضلعانِ فإنَّ النسبةَ بينَ محيطَيْهِما تساوي النسبةَ بينَ الأضلاعِ المتناظرةِ 

اذا كان KLMN ~ PQRS فإن: 

$\frac{PQ + QR + RS + SP}{KL + LM + MN + NK}=\frac{PQ }{KL}=\frac{QR}{LM}=\frac{RS}{MN}=\frac{SP}{NK}$

 

مثال 4: منَ الحياةِ : مسابحُ: مسبحٌ في صالةٍ رياضيةٍ، طولُهُ 50m وَعَرضُهُ 25m بُنِيَ مسبحٌ آخَرُ  في الصالةِ مشابهٌ لِلمسبحِ القديمِ طولُهُ 40m جِدُ محيطَ المسبحِ الجديدِ.

الْخُطْوَةُ 1 :أَجِدُ عاملَ المقياسِ: 

بِما أنَّ المسبحَ الأولَ يشابهُ المسبحَ الثانيَ فَإنَّ عاملَ المقياسِ يساوي النسبةَ بينَ أطوالِ الأضلاعِ المتناظرةِ $\frac{40}{50}=\frac{4}{5}$ إذنْ، عاملُ المقياسِ $\frac{4}{5}$

الْخُطْوَةُ 2 :أَجِدُ محيطَ المسبحِ القديمِ:

$$\begin{gathered} \mathrm{P} = 2\mathrm{l} + 2\mathrm{w} \\ =2\left(50\right)+2\left(20\right) \\ =150 \end{gathered}$$             محيط المستطيل وبتعويض القيم L,W 

إذنْ، محيطُ المسبحِ القديمِ 150m

الْخُطْوَةُ 3: أَجِدُ محيطَ المسبحِ الجديدِ بِاستعمالِ عاملِ المقياسِ:

$\frac{\mathrm{x}}{150}=\frac{4}{5}$                      النسبةُ بينَ محيطَيْ مضلعَينِ متشابهَينِ

$$\begin{gathered} 5\mathrm{x}=600 \\ \mathrm{x}=120 \end{gathered}$$                       بالضرب التبادلي نجد قيمة x والتي تمثل محيط المسبح الجديد 

إذنْ، محيطُ المسبحِ الجديدِ 120m