حلول أسئلة أتحقق من فهمي
:ABCD ~ EFGH في الشكلِ المجاورِ
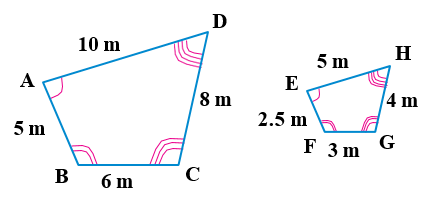
3)أكتبُ أزواجَ الزوايا المتناظرةِ.
∠A ≅ ∠E , ∠B ≅ ∠F , ∠C ≅ ∠G , ∠D ≅ ∠H
4)أَجِدُ النسبةَ بينَ طولَيْ كلِّ ضلعَينِ متناظِرَينِ بِأبسطِ صورةٍ، ثمَّ أكتبُ جملةَ التناسُبِ.
اذن جملة التناسب هي :
2)أبيّنُ ما إذا كانَ المستطيلانِ المجاورانِ متشابهَينِ، : ثمَّ أَجِدُ عاملَ المقياسِ

الزوايا المتناظرة في المستطيلان متطابقة جميعها قائمة،
أَجِدُ النسبةَ بينَ طولَيْ كُلِّ ضلعَينِ متناظِرَينِ:
والأضلاع المتناظرة متناسبة ،عامل القياس
m أَجِدُ قيمةَ المتغيِّرِ ، ABCD ~ WXYZ في الشكلِ المجاورِ
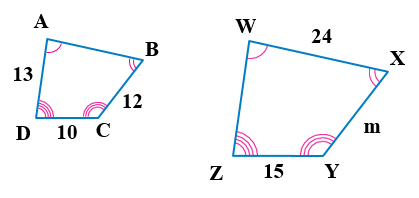
x نكتب تناسباً ونعوض القيم لايجاد المتغير
بالضرب التبادلي بعد تعويض القيم x=18
نافذتانِ زجاجيتانِ متشابهتانِ على شكلِ مضلَّعٍ خماسيٍّ، أَجِدُ محيطَ النافذةِ الصغيرةِ.

الْخُطْوَةُ 1 :أَجِدُ عاملَ المقياسِ:
بِما أنَّ النافذتان متشابهتان فإن عاملَ المقياسِ يساوي النسبةَ بينَ أطوالِ الأضلاعِ المتناظرةِ
الْخُطْوَةُ 2 :أَجِدُ محيطَ النافذة الكبيرة
محيط المضلع الخماسي يساوي مجموع اضلاعه
الْخُطْوَةُ 3: أَجِدُ محيطَ النافذة الصغيرة بِاستعمالِ عاملِ المقياسِ:
النسبةُ بينَ محيطَيْ مضلعَينِ متشابهَينِ
بالضرب التبادلي نجد قيمة x والتي تمثل محيط النافذة الصغيرة
اذن محيطَ النافذة الصغيرة = 46 متر
حلول أسئلة أتدرب وأحل المسائل
أكتبُ أزواجَ الزوايا المتناظرةِ، ثمَّ أَجِدُ عاملَ المقياسِ لكلٍّ مِنْ أزواجِ المضلعاتِ المتشابهةِ الآتيةِ:
1)

∠A ≅ ∠H , ∠B ≅ ∠J , ∠C ≅ ∠K , ∠D ≅ ∠L :الزوايا المتناظرة
عامل المقياس :
2)
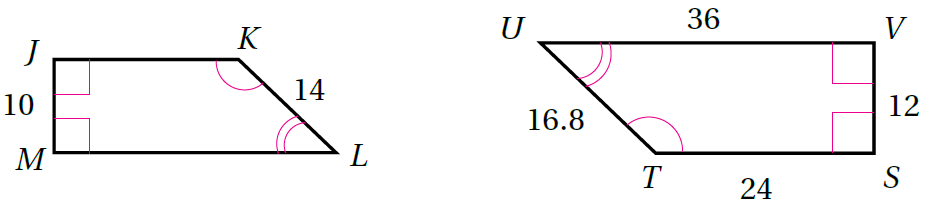
∠J ≅ ∠S , ∠M ≅ ∠V , ∠L≅ ∠U , ∠K ≅ ∠T :الزوايا المتناظرة
عامل المقياس :
أبيّنُ ما إذا كانَ كلُّ زَوجٍ مِنَ المضلعاتِ الآتيةِ متشابهَينِ، ثمَّ أَجِدُ عاملَ المقياسِ لِلمتشابِهِ منها:
3)
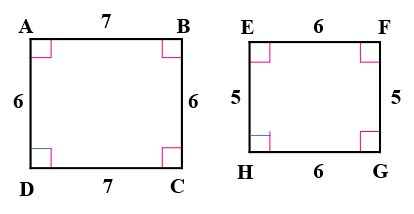
الزوايا المتناظرة متطابقة
نجد النسبة بين الاضلاع :
المضلعان غير متشابهيين لأن الاضلاع غير متناسبة
4)

الزوايا المتناظرة متطابقة
نجد النسبة بين الاضلاع :
المضلعان متشابهان عامل المقياس
5)أَجِدُ قيمةَ كلٍّ مِنَ المتغيِّرَينِ x,y في زَوجِ المضلعاتِ المتشابهِ الآتي:
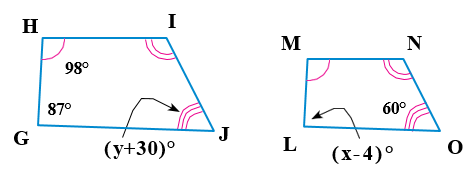
من تطابق الزاويا المتناظرة نجد قيمة x
من تطابق الزاويا المتناظرة نجد قيمة y
6)أثاثٌ: يبيّنُ الشكلُ المجاورُ طاولتَينِ متشابهتَينِ إِحداهُما مخصَّصةٌ لِلأطفالِ وَالأُخرى لِلكبارِ. أَجِدُ طولَ طاولةِ الأطفالِ
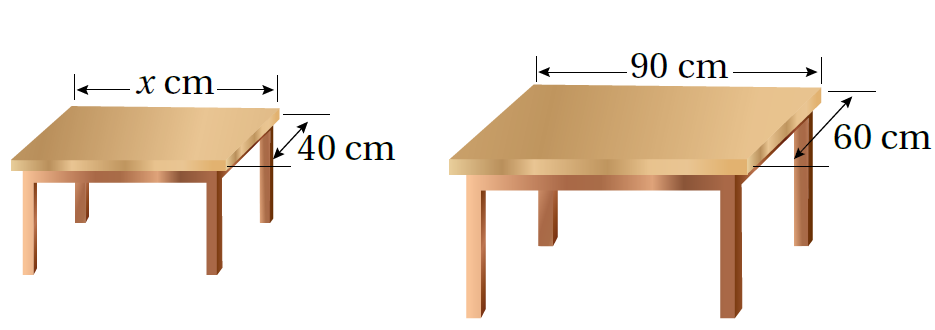
نكتب تناسب ونعوض القيم لايجاد قيمة x والتي تمثل طول طاولة الاطفال
7) حديقةٌ: وقفَتْ مَيارُ بِجانبِ لعبةٍ في حديقة إذا كانَ طولُ ميارَ 5ft وَطولُ ظِلِّها 4ft وَكانَ طولُ ظِلِّ اللعبةِ 4.8ft فَأَجِدُ ارتفاعَ اللعبةِ، علمًا أنَّ المثلثاتِ متشابهةٌ.
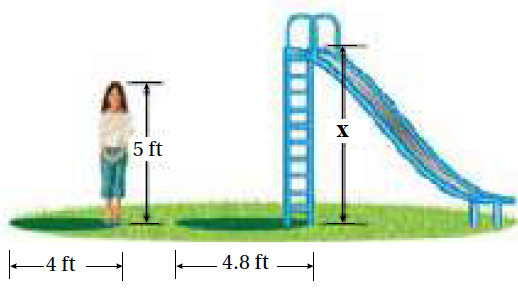
بما أن المثلثات متشابه نكتب النسب بين الأضلاع لايجاد ارتفاع اللعبة x
اذن ارتفاع اللعبة 6ft
أَجِدُ: ، JKLM ~ EFGH في الشكلِ المجاورِ
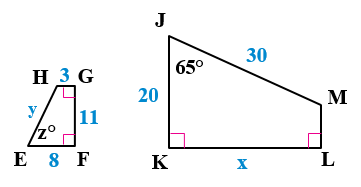
8) عاملَ المقياسِ.
9)قيمةَ كلٍّ مِنَ المتغيِّراتِ x و y و z
قيمة المتغير x ,والتي تمثل طول القطعة KL
قيمة المتغير y , والتي تمثل طول القطعة EH
قيمة المتغير z , والتي تمثل الزاوية
∠E≅ ∠J
10) محيطَ كلِّ مضلعٍ.
محيط المضلع الأصغر
محيط المضلع الأكبر باستخدام معامل القياس
11)تحدٍّ: مستطيلانِ متشابهانِ، النسبةُ بينَ أضلاعِهِما المتناظرةِ هِيَ 1:4 أَجِدُ النسبةَ بينَ مساحتَيهِما.
طول الضلع في المستطيل الثاني = 4 × طول الضلع في المستطيل الأول
مساحة الأول = الطول(X) × العرض(Y)
= XY
مساحة الثاني = 4الطول الاول(X) ×4 العرض الاول(Y)
= 16XY
النسبة بين المساحتين 1:16
12) أكتشفُ الخطأَ: أحدّدُ الخطأَ، وَأصححُهُ في كيفيةِ إيجاد محيط ΔZWY علمًا أنَّ ΔABC وَ ΔZWY متشابهانِ
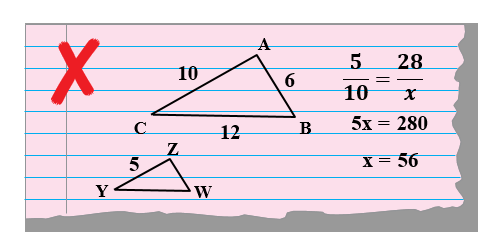
جملة التناسب خاطئة
تصحيح : ومنه المحيط x=14
13)تبريرٌ: في الشكلِ المجاورِ، أغيّرُ موقعَ رأسٍ واحدٍ في الشكلِ (1) لِيصبحَ الشكلانِ (1) و (2) متشابهَينِ. أبرّرُ إجابتي.
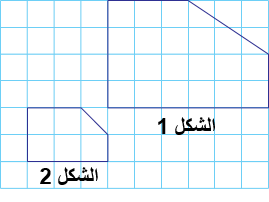
الحل : لجعل الشكلين متشابهين يجب أن تكون نسب الاضلاع المتناظرة جميعها متناسبة وتساوي
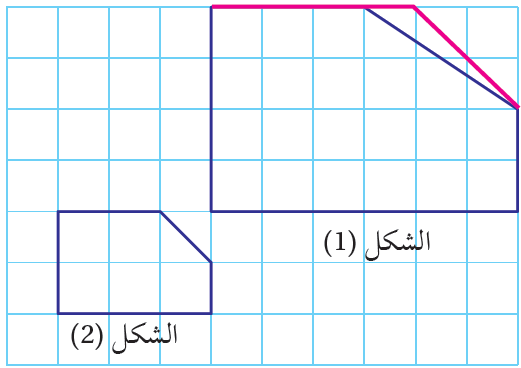
14) تبريرٌ: أبيّنُ صحةَ العبارةِ الآتيةِ،"أيُّ مضلعَينِ منتظمَينِ لَهُما العددُ نفسُهُ مِنَ الأضلاعِ متشابهانِ." مبررًا إجابتي.
العبارة صحيحة ، لأن المضلع المنتظم جميع زواياه متساوية ومنه الزوايا المتناظرة في المضلعين متطابقة ونسبة طول أي ضلع من المضلع الأول إلى طول أي ضلع من المضلع الثاني ثابتة.
15) تبريرٌ: في الشكلِ المجاورِ ΔXPZ ~ ΔTPR أَجِدُ طولَ وَأبرّرُ إجابتي.

تنصيف المثلثين المتشابهيين باستخدام خط مستقيم يتنج عنه مثلثات متشابهة
16)أكتبُُ كيفَ أحدّدُ ما إذا كانَ مضلعانِ متشابهَينِ أَمْ لا؟
أتأكد من أن الزوايا المتناظرة متطابقة، وأطوال أضلاعهما المتناظرة متناسبة.
حلول أسئلة كتاب التمارين
أَجِدُ عاملَ مقياسٍ لكلٍّ مِنْ أزواجِ المثلَّثاتِ المتشابهةِ الآتيةِ:
1)
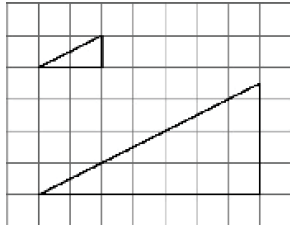
الحل: نجد عامل القياس من عدد المربعات
2)
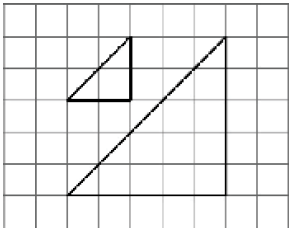
الحل: نجد عامل القياس من عدد المربعات
3)أظلّلُ الأشكالَ المشابهةَ لِلشكلِ S
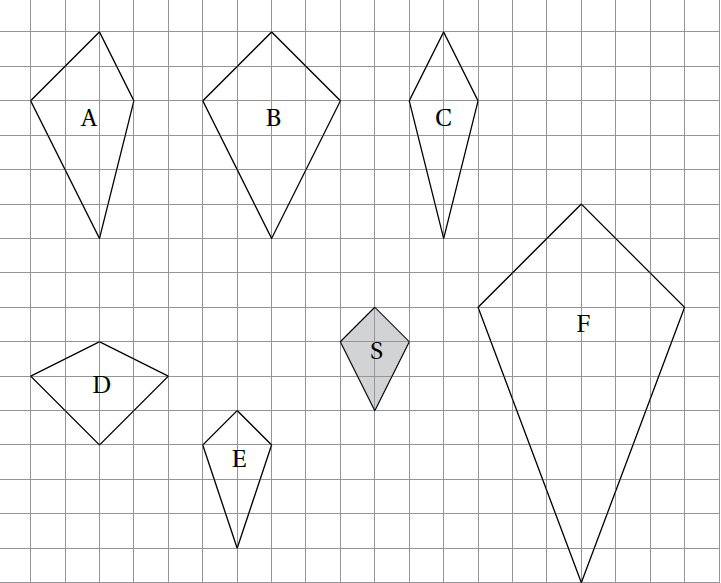
الحل: الشكل الذي يحقق مفهوم التشابه هو B
في كلٍّ مِنْ أزواجِ المضلَّعاتِ المتشابهةِ الآتيةِ: x أَجِدُ قيمةَ
4)
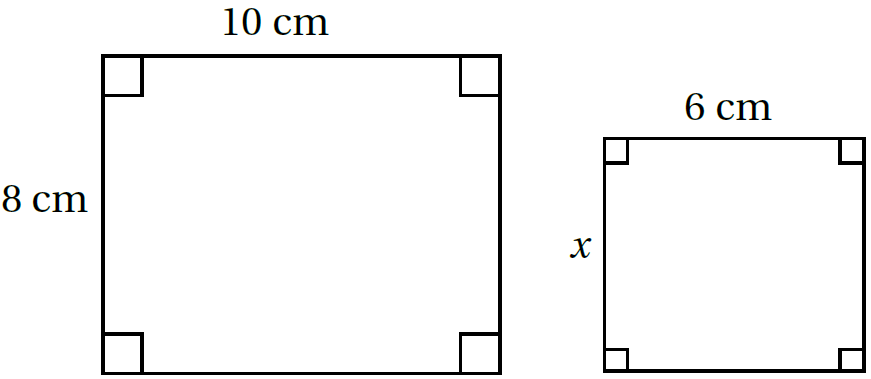
الحل:
5)
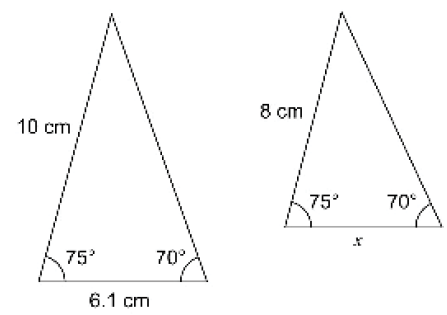
الحل:
6) في الشكلِ المجاورِ ΔABC~ΔDEB أَجِدُ طولَ AC
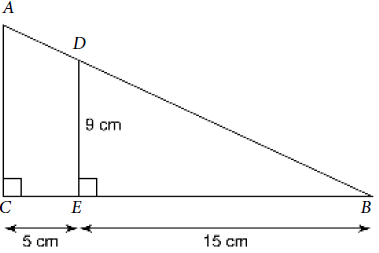
الحل: