رياضيات 7 فصل ثاني

حلول أسئلة اتحقق من فهمي

يمثّلُ الجدولُ المجاورُ علاقةً بينَ المتغيّرَينِ x,y 

y	x
1	3
2	6
3	9
???	12

3) أبيّنُ أنَّ العلاقةَ بينَ x وَ y  تمثّلُ تغيّرًا طرديًّا، ثمَّ أَجِدُ ثابتَ التغيّرِ $k$

أَجِدُ النسبةَ $\frac{y}{x}$ لِلقيمِ المتناظرةِ جميعِها

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{1}{3} , \frac{2}{6} = \frac{1}{3} , \frac{3}{9} =\frac{1}{3}$ 

 تمثل العلاقة بينَ المتغيّرَينِ x,y تغيّرًا طرديًّا، لأن النسب متساوية، والزيادة في أحدهما تؤدي إلى زيادة في الأخرى. وثابتُ التغيّرِ   $\mathrm{k}=\frac{1}{3}$

4) أكتبُ معادلةَ التغير الطرديِّ، ثم أَجِدُ القيمةَ المجهولةَ في الجدولِ 

   $\mathrm{y}=\frac{1}{3}\mathrm{X}$        أكتبُ معادلةَ التغير الطرديِّ

$\mathrm{y}=\frac{1}{3}\left(12\right)$        أُعوّضُ X=12 في المعادلةِ

        $y=4$        أَجِدُ الناتجَ

 

يبيّنُ الجدولُ المجاورُ علاقةَ تناسُبٍ بينَ الزمنِ بالثواني اللازمِ لضخِّ عددٍ مِنْ لتراتِ البنزينِ في إحدى محطاتِ الوَقودِ: 

الزمن s	عدد اللترات
74	9.25
84	10.5
96	12
136	17

3) أبيّنُ أنَّ العلاقةَ بينَ عددَ اللتراتِ والزمنَ تمثّلُ تغيّرًا طرديًّا، ثمَّ أَجِدُ ثابتَ التغيّرِ  k  

أَجِدُ النسبةَ $\frac{\mathrm{y}}{\mathrm{x}}$ لِلقيمِ المتناظرةِ جميعِها

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{9.25}{74} =\frac{10.5}{84} = \frac{12}{96} =\frac{17}{136}=0.125$

 y,x متناسبان طرديا لأن النسب متساوية، والزيادة في أحدهما تؤدي إلى زيادة في الأخرى. وثابتُ التناسُبِ k=0.125

4) أكتبُ معادلةَ التغير الطرديِّ.

y=0.125X

 

يبيّنُ التمثيلُ البيانيُّ المجاورُ علاقةَ تغيّرٍ طرديٍّ بينَ عددِ أكوابِ الطحينِ وعددِ أكوابِ الحليبِ في وصفةٍ لإعدادِ الكعكِ. أكتبُ معادلةً هذا التغيّرِ الطرديِّ

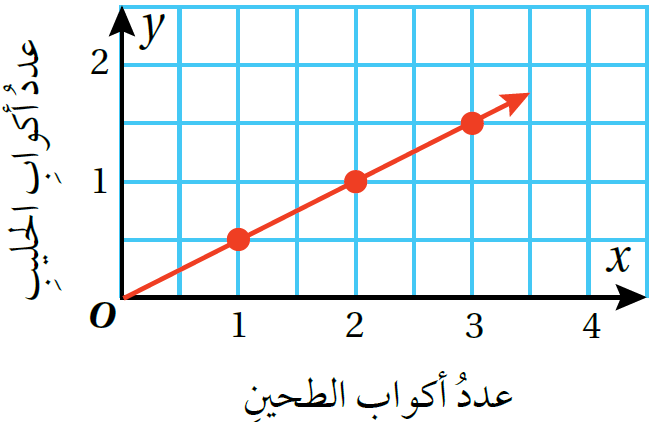
من الرسم البياني أجد ثابت التغير  y عندما x=1  $\mathrm{k}=\frac{1}{2}$ 

 أكتبُ معادلةَ التغير الطرديِّ  $\mathrm{y}=\frac{1}{2}\mathrm{x}$

 

 

 

 يزدادُ طولُ نبتةٍ بمقدارِ 1.5cm كلَّ أُسبوعٍ:

5) أبيّنُ أنَّ العلاقةَ تمثّلُ تغيرًا طرديًّا.

نكتب جدول يمثل العلاقة 

الزمن (اسبوع)	1	2	3
الزيادة في الطول cm	1.5	3	4.5

 

 

أَجِدُ النسبةَ $\frac{y}{x}$ لِلقيمِ المتناظرةِ جميعِها

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow 1.5 ,\frac{3}{2}=1.5,\frac{4.5}{3}=1.5$   

 تمثل العلاقة بينَ الزمن والزيادة في طول النبتة تغيّرًا طرديًّا لأن النسب متساوية، والزيادة في أحدهما تؤدي إلى زيادة في الأخرى.

6) أكتبُ معادلةً لهذهِ العلاقةِ.

ثابتُ التغير   k=1.5

أكتبُ معادلةَ التغير الطرديِّ     y=1.5x      

---

---

حلول أسئلة أتدرب وأحل المسائل

أحددُ أيُّ العلاقاتِ الخطّيةِ الآتيةِ تمثّلُ تغيرًا طرديًّا، وإنْ كانَتْ كذلكَ أَجِدُ ثابتَ التغير لَها:

1)  

أَجِدُ النسبةَ $\frac{\mathrm{y}}{\mathrm{x}}$  لِلقيمِ المتناظرةِ جميعِها

y	x
5	2
10	4
15	6

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{5}{2}=\frac{10}{4} = \frac{15}{6}=2.5$ 

  تمثل العلاقة بينَ المتغيّرَينِ x,y   تغيّرًا طرديًّا لأن النسب متساوية، والزيادة في أحدهما تؤدي إلى زيادة في الأخرى. k=2.5وثابت التغيّر   

 

2)

 أَجِدُ النسبةَ$\frac{\mathrm{y}}{\mathrm{x}}$ لِلقيمِ المتناظرةِ جميعِها

y	x
60	185
32	235
40	275

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{60}{185}\approx 0.32 , \frac{32}{235}\approx 0.14 , \frac{40}{275}\approx 0.15$

 العلاقة بينَ المتغيّرَينِ x,y  لا تمثل تغيّرًا طرديًّا لأن النسب غير متساوية.

 

3)

 أَجِدُ النسبةَ $\frac{\mathrm{y}}{\mathrm{x}}$ لِلقيمِ المتناظرةِ جميعِها

y	x
6	3
8	4
10	5

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{6}{3}=\frac{8}{4} = \frac{10}{5}=2$

 تمثل العلاقة بينَ المتغيّرَينِ

 

x,y  تغيّرًا طرديًّا لأن النسب متساوية، والزيادة في أحدهما تؤدي إلى زيادة في الأخرى. وثابت التغيّر  k=2

 

 

 

 

 

 

 

 

 

4) 

أَجِدُ النسبةَ$\frac{y}{x}$ لِلقيمِ المتناظرةِ جميعِها

y	x
6	4
8	5
10	6

$\frac{\mathbf{y}}{\mathbf{x}} \Rightarrow \frac{6}{4}=1.5 , \frac{8}{5}=1.6 , \frac{10}{6}=1.6$

العلاقة بينَ المتغيّرَينِ x,y  لا تمثل تغيّرًا طرديًّا، لأن النسب غير متساوية.

 

أكتبُ معادلةَ التغير الطرديِّ في كلٍّ ممّا يأتي:

5) 

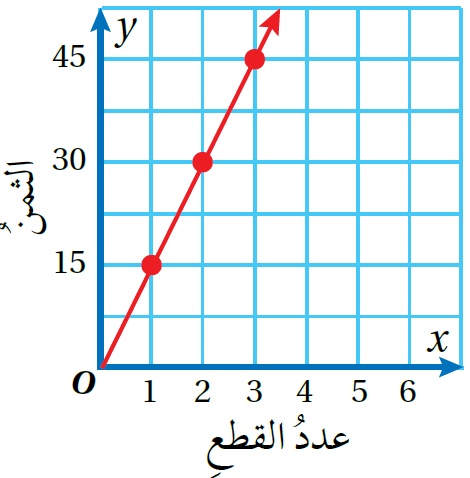
من الرسم البياني أجد ثابت التغير

$\mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{15}{1}=15$

 أكتبُ معادلةَ التغير الطرديِّ

y=15x

 

6) 

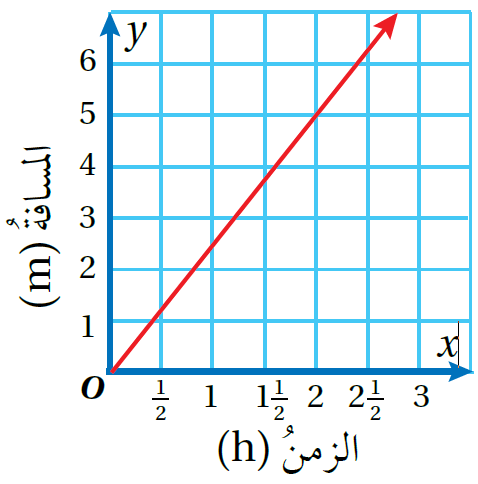
من الرسم البياني أجد ثابت التغير k ويمثل y عندما x=1 

2.5=k

 أكتبُ معادلةَ التغير الطرديِّ

y=2.5x

 

 

 

 

 طائراتٌ: انطلقَتْ طائرتانِ عموديَّتانِ A و B  في الوقتِ نفسِهِ، ويمثّلُ الشكلُ المجاورُ العلاقةَ بينَ ارتفاعِ كلٍّ منهُما بالأمتارِ والزمنِ بالدقائقِ.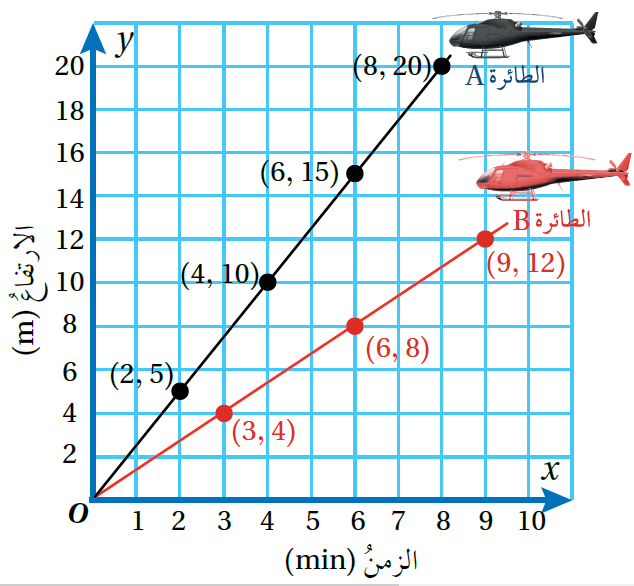

7) هل توجَدُ علاقةُ تغير طرديٍّ بينَ ارتفاعِ كلِّ طائرةٍ والزمنِ؟ أبرّرُ إجابتي.

توجد علاقة تغيّر طردي في الحالتين لأن التمثيل البياني في كل منهما مستقيم يمر بنقطة الأصل.

8) إذا كانَتِ العلاقةُ تمثّلُ تغيرًا طرديًّا؛ أَجِدُ ثابتَ التغير.

$\mathrm{B}\Rightarrow \mathrm{k} =\frac{\mathrm{y}}{\mathrm{x}}=\frac{4}{3}$

$\mathrm{A}\Rightarrow \mathrm{k} =\frac{\mathrm{y}}{\mathrm{x}}=\frac{5}{2}$

9) أوضّحُ سببَ ارتفاعِ الطائرةِ A  بصورةٍ أسرعَ مِنَ الطائرةِ B

لأن ثابت التغير (معدّل الوحدة) للطائرة A أكبر منه للطائرة B 

 

يمثّلُ كلٌّ مِنَ الجدولَينِ الآتيَينِ علاقةَ تغير طرديٍّ. أَجِدُ القِيَمَ المجهولةَ في كلٍّ منهُما:

10) 

       

12	6	4	2	x
30	15	10	5	y

   أجد ثابت التغير و أكتبُ معادلةَ التغير الطرديِّ ثم بالتعويض في المعادلة اجد القيم المجهولة 

   $\mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{30}{12}=2.5 \Rightarrow \mathrm{y}=\mathrm{kx} = 2.5\mathrm{x}$

 

11)

16	12	10	8	x
24	18	15	12	y

    أجد ثابت التغير و أكتبُ معادلةَ التغير الطرديِّ ، ثم بالتعويض في المعادلة اجد القيم المجهولة 

   $\mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{12}{8}=1.5 \Rightarrow \mathrm{y}=\mathrm{kx} = 1.5\mathrm{x}$

 

 

12) رحلاتٌ: نظّمَتْ مدرسةُ ريّانَ رحلةً إلى غاباتِ جرشَ وعجلونَ، بحيثُ يرافقُ كلَّ 14 طالبًا معلمٌ واحدٌ. أكتبُ معادلةً تمثّلُ هذهِ العلاقةَ، وأمثّلُها بيانيًّا.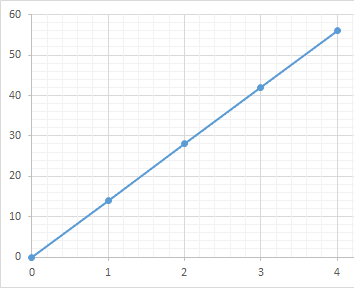

نكتب جدول يمثل العلاقة 

عدد المعلمين x	1	2	3
عدد الطلبة y	14	28	42

 

 

 أجد ثابت التغير و أكتبُ معادلةَ التغير الطرديِّ  

$\mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{14}{1}=14 \Rightarrow \mathrm{y}=\mathrm{kx} = 14\mathrm{x}$

 

 

 

 

يبيّنُ الشكلُ المجاورُ عددَ ضرباتِ جناحَيْ طائرِ الطنّانِ بالنسبةِ للزمنِ بالثواني (s)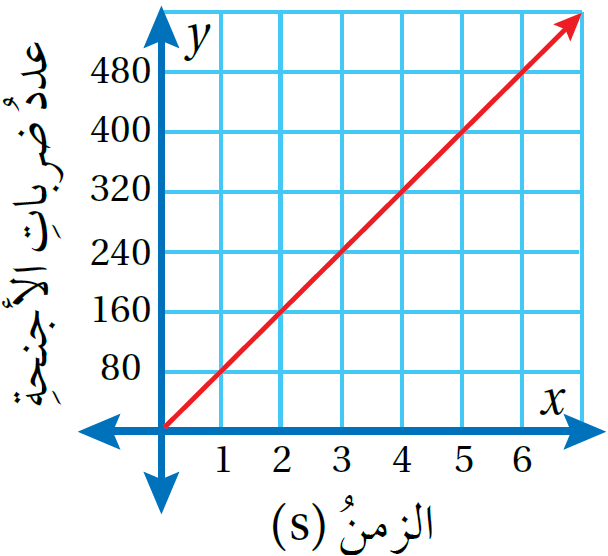 

13) ماذا تمثّلُ النقطةُ (2,160) 

عدد ضرباتِ جناحَيْ طائرِ الطنّانِ (160) في زمن 2s                                                                    

14) أكتبُ معادلةً تمثّلُ هذهِ العلاقةَ.

 أجد ثابت التغير و أكتبُ معادلةَ التغير الطرديِّ  

$\mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{80}{1}=80 \Rightarrow \mathrm{y}=\mathrm{kx} = 80\mathrm{x}$

15) أَجِدُ عددَ ضرباتِ الجناحِ في 6 دقائقَ.

 أُعوّضُ الزمن في المعادلةِ - مع الانتباه على تحويل ال6 دقائق الى ثواني بالضرب ب 60 ثانية 

y=80x

y=80(360)

y=28800

 

يمثّلُ الشكلُ المجاورُ العلاقةَ بينَ الزمنِ بالساعاتِ (h)  والمسافةِ بالكيلومتراتِ الّتي يقطعُها متسابقُ رياضةِ تسلّقِ جبالٍ:

16) أكتبُ معادلةً تمثّلُ هذهِ العلاقةَ.

من الرسم البياني أجد ثابت التغير و أكتبُ معادلةَ التغير الطرديِّ  

$\mathrm{k}=\frac{\mathrm{y}}{\mathrm{x}}=\frac{6}{5} \Rightarrow \mathrm{y}=\mathrm{kx} =\frac{6}{5}\mathrm{x}$

17) كَمْ ساعةً يحتاجُ المتسابقُ لقطعِ مسافةِ 30Km

 أُعوّضُ المسافة في المعادلةِ لايجاد الزمن عندما y=30 

$$\begin{gathered} \mathrm{y}=\frac{6}{5}\mathrm{x} \\ 30=\frac{6}{5}\mathrm{x} \\ \mathrm{x}=25 \Rightarrow \mathrm{ساعة} 25 \mathrm{بعد} \end{gathered}$$         

 

18) مسألةٌ مفتوحةٌ: أكتبُ مسألةً حياتيةً يكونُ ثابتُ التغير فيها 6Km

يوجد إجابات متعددة 

إجابة مقترحة : تستهلك سيارة كمية 1 لتر من الوقود عند قطع مسافة 6km ، علاقة استهلاك الوقود مع المسافة المقطوعة تمثل علاقة تغير طردي ثابت التغير فيها 6Km

19) تبريرٌ: إذا كانَ ثابتُ تغير العلاقةِ الطرديةِ الممثَّلةِ في الجدولِ المجاورِ يساوي 5. أَجِدُ القِيَمَ المجهولةَ في الجدولِ، وأبرّرُ خطواتِ الحلِّ جميعَها.

السعر (JD)	الزمن (h)
50=X	10
100= Y	20
150	30=Z

       أكتبُ معادلةَ التغير الطرديِّ y=5x 

       أُعوّضُ الزمن x=10 في المعادلة لايجاد X

       أُعوّضُ الزمن x=20 في المعادلة لايجاد Y

                                              أُعوّضُ السعر y=150 في المعادلة لايجاد Z

 

20) أكتبُُ كيفَ أحددُ ما إذا كانَتِ العلاقةُ بينَ متغيّرَينِ تمثّلُ علاقةَ تغير طرديٍّ؟

إذا كانَتِ النسبةُ بينَ جميعِ قِيَمِهِما ثابتة حسب المعادلة y=kx  حيثُ تؤدي الزيادةُ في إحدى الكمّيتَينِ إلى زيادةِ الأُخرى وكذلكَ العكسُ

---

---

حلول أسئلة كتاب التمارين 

يبيّنُ الجدولُ المجاورُ علاقةً بينَ عددِ عبوّاتِ عصيرٍ (x) وثمنها (y)  

؟؟	5	2	1	X
1.6	1	0.4	0.2	Y

1) أبيّنُ أنَّ العلاقة بين المتغيرين x,y تمثل تغير طردي، ثمَّ أَجِدُ ثابتَ التغير k

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{0.2}{1}=\frac{0.4}{2} = \frac{1}{5}=0.2 \Rightarrow \mathrm{k}=0.2$
2) أكتبُ معادلةَ التغير الطرديِّ.

     y=0.2x
3) أَجِدُ القيمةَ المجهولةَ في الجدولِ.

$$\begin{gathered} \mathrm{y}=0.2\mathrm{x} \\ 1.6=0.2\mathrm{x} \\ \mathrm{x}=8 \end{gathered}$$

تسيرُ شاحنةٌ بِسرعةٍ ثابتةٍ بِمعدَّلِ 60km/h   

4) أكملُ الجدولَ الآتِيَ الّذي يبيّنُ العلاقةَ بينَ الزمنِ بِالساعاتِ (h) والمسافة (d km)

من العلاقة المعطاه 

         

2	1.5	1	0.5	h
120	90	60	30	d

 

 

 

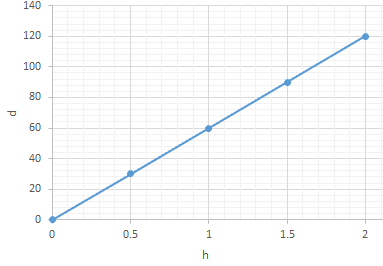
5) أمثّلُ العلاقةَ بيانيًّا.

6) أبيّنُ أنَّ العلاقةَ تمثّلُ تغيرًا طرديًّا.

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{30}{0.5}=\frac{60}{1} = \frac{90}{1.5}=\frac{120}{2}=60$

  تمثل العلاقة بينَ المتغيّرَينِ  x,y  تغيّرًا طرديًّا،لأن النسب متساوية، k=60

7) أكتبُ معادلةَ التغير الطرديِّ.

y=60x

 

يمزِجُ صائغٌ الذهبَ مَعَ البلاتينيومِ لِصنعِ الذهبِ الأبيضِ. يبيّنُ التمثيلُ البيانيُّ  المجاورُ العلاقةَ بينَ كمّيّةِ الذهبِ (g) بالغِرامِ وَكمّيّةِ البلاتينيومِ (p) الّتي يستعملُها الصائغُ بالغِرامِ أيضًا:

8)أكملُ الجدولَ الآتِيَ:

 

من الرسم البياني

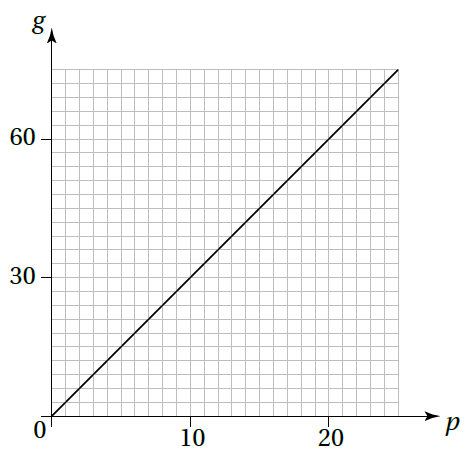
20	15	10	5	0	p
60	45	30	15	0	g

9) أكتبُ معادلةً تمثّلُ هذهِ العلاقةَ.

g=3p

10) أستعملُ المعادلةَ لِيجادِ كمّيّةِ البلاتينيومِ الّتي يحتاجُ الصائغُ إلى مَزجِها مَعَ 10.5g مِنَ الذهبِ.

$$\begin{gathered} \mathrm{g}=3\mathrm{p} \\ 10.5=3\mathrm{p} \\ \mathrm{p}=3.5 \end{gathered}$$

 

 

11) يبيّنُ التمثيلُ البيانيُّ المجاورُ علاقةَ تغير طرديٍّ بينَ حجمِ مكعّبٍ مِنَ الفضّةِ (V cm³) وَكتلتِهِ (m Kg)  أَجِدُ كتلةَ مكعّبِ فضّةٍ طولُ ضلعِهِ 4.8cm مقرّبًا إجابتي لِقربِ منزلتَينِ عشريّتَينِ.

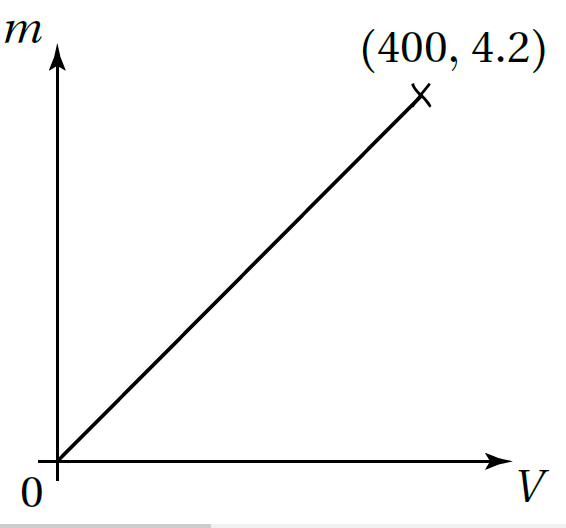
نجد قيمة x مستعيناً بالنقطة المعطاه في الرسم البياني ( مع الانتباه اننا سنعوض حجم المكعب 4.8³)

$$\begin{gathered} \frac{4.2}{400}=\frac{\mathrm{x}}{{(4.8)}^3} \\ \mathrm{x}=1.16 \mathrm{kg} \end{gathered}$$

 

 

 

 

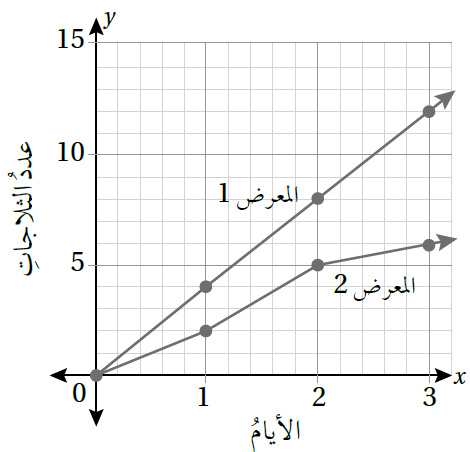
يبيّنُ التمثيلُ البيانيُّ المجاورُ العلاقةَ بينَ عددِ الثلاجاتِ المبيعَةِ في معرضَينِ خلالَ 3 أيامٍ:

12) هلْ توجَدُ علاقةُ تغير طرديٍّ بينَ عددِ الثلاجاتِ المبيعةِ وَعددِ الأيامِ لِكلِّ معرِضٍ؟ أبرّرُ إجابتي.

• توجد علاقة تغيّر طردي في المعرض 1 لأن التمثيل البياني مستقيم يمر بنقطة الأصل.
• لا توجد علاقة تغيّر طردي في المعرض 2 لأن لأن النقاط لا تقع على مستقيم واحد.

13) أَجِدُ ثابتَ التغير وَمعادلتَهُ للعلاقةِ الّتي تمثلُ تغيرًا طرديًّا.

في المعرض الأول :

 $$\begin{gathered} \frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{4}{1}=4\Rightarrow \mathrm{k}=4 \\ \mathrm{y}=4\mathrm{x} \end{gathered}$$

14) أَجِدُ مبيعاتِ المعرضِ في اليومِ السادسِ اعتمادًا على العلاقةِ الّتي تمثلُ تغيرًا طرديًّا. 

$$\begin{gathered} \mathrm{y}=4\mathrm{x} \\ \mathrm{y}=4\left(6\right) \\ \mathrm{y}=24 \end{gathered}$$

15) هلْ يمكنُ التنبّؤُ بِعددِ الثلاجاتِ الّتي بيعَتْ في اليومِ الرابعِ اعتمادًا على العلاقةِ التي لا تمثلُ تغيرًا طرديًّا؟ أبرّرُ إجابتي

لا, لأن نسبة المبيعات غير ثابتة في الأيام الثلاثة الأولى.

 

يخلِطُ محلُّ بيعِ مكسَّراتٍ الجَوزَ وَالبُندقَ بِنسبةِ 5:2 وَيعبّئُها في أكياسٍ. إذا احتوى كيسٌ على w Kg مِنَ الجَوزِ و h Kg مِنَ البُندقِ:

16) أكتبُ معادلةً تمثّلُ العلاقةَ بينَ كمّيّةِ الجَوزِ وَكمّيّةِ البُندقِ.

$\mathrm{h}=\frac{2}{5}\mathrm{w}$
17) أحوطُ التمثيلَ البيانيَّ الّذي يناسِبُ المعادلةَ الّتي كتبْتُها، مبررًا إجابتي.

 

 

 

 

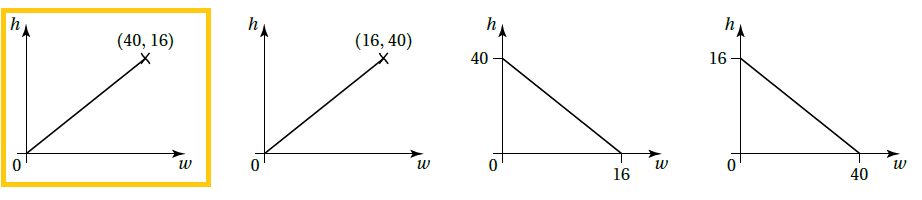
لان النقطة (40,16) تحقق المعادلة $\mathrm{h}=\frac{2}{5}\mathrm{w}$