أتحقق من فهمي (مثال 1) :
3) أجد النسبة بين طول أحد الأضلاع في الصورة إلى طول ضلع مناظر له في الشكل الأصلي كالتالي :
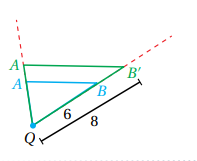
لاحظ أن الشكل تعرض إلى تكبير
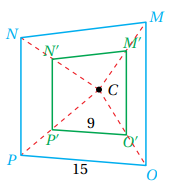
4) أجد النسبة بين طول أحد الأضلاع في الصورة إلى طول ضلع مناظر له في الشكل الأصلي كالتالي :
لاحظ أن الشكل تعرض إلى تكبير.
أتحقق من فهمي (مثال 2) :
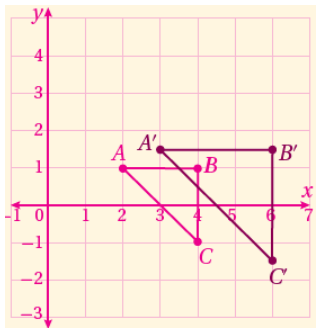
3) بعد ضرب إحداثيات الشكل الأصلي ب 1.5 تنتج صورة إحداثياتها : 𝐴 ′ (3, 1.5),𝐵 ′ (6, 1.5), 𝐶 ′ (6, −1.5)
ويمكن تمثيل الصورة كما هو موضح في الرسم المجاور .
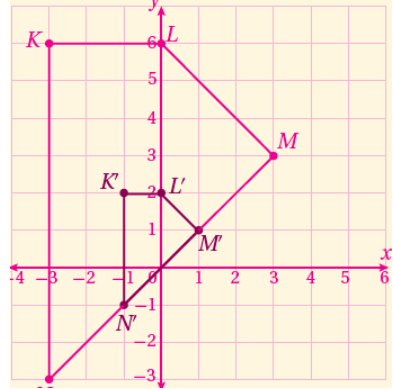
4)بعد ضرب إحداثيات الشكل الأصلي ب تنتج صورة إحداثياتها K'(-1,2), L'(0,2), M'(1,1), N'(-1,-1)
ويمكن تمثيل الصورة كما هو موضح في الرسم المجاور
أتحقق من فهمي (مثال 3) :
3) بعد ضرب إحداثيات الشكل الأصلي ب تنتج صورة إحداثياتها : 𝑃 ′ (−2, −4),𝑄 ′ (−6, −2), 𝑅 ′ (−2, 6)
بعد الرسم لاحظ أن الشكل قد تعرض لتكبير ودوران بمقدار .
أتدرب وأحل مسائل ص(110-111).
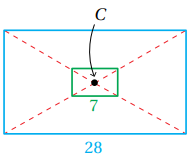
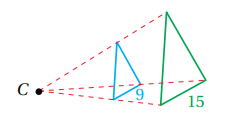
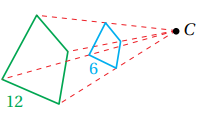
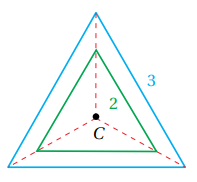
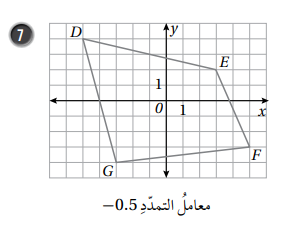
إذا كان الشكل باللون الأخضر صورة للشكل باللون الأزرق تحت تأثير تمدد مركزه C ، فأجد معامل التمدد في كل مما يأتي ، ثم أحدد ما إذا كان التمدد تكبيراً أم تصغيراً .
1) أجد النسبة بين طول أحد الأضلاع في الصورة إلى طول ضلع مناظر له في الشكل الأصلي كالتالي : ، بما أن K أصغر من 1 وأكبر من 0 فإن الشكل سيتعرض إلى تصغير
2) أجد النسبة بين طول أحد الأضلاع في الصورة إلى طول ضلع مناظر له في الشكل الأصلي كالتالي : ، بما أن K أكبر من 1 فإن الشكل سيتعرض إلى تكبير .
3) أجد النسبة بين طول أحد الأضلاع في الصورة إلى طول ضلع مناظر له في الشكل الأصلي كالتالي : ، بما أن K أكبر من 1 فإن الشكل سيتعرض إلى تكبير
4) أجد النسبة بين طول أحد الأضلاع في الصورة إلى طول ضلع مناظر له في الشكل الأصلي كالتالي : ، بما أن K أصغر من 1 وأكبر من 0 فإن الشكل سيتعرض إلى تصغير.
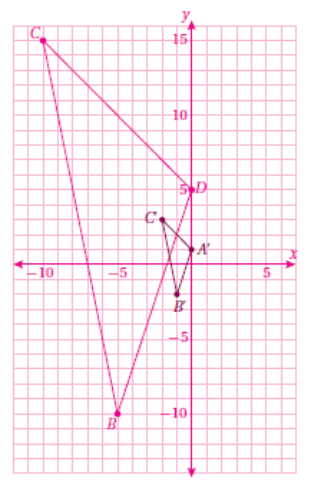
5) أقوم بضرب إحداثيات الشكل الأصلي ب 1.5 لتنتج صورة إحداثياتها :
Q'(4.5, 1.5), P'(1.5, 4.5), R'(1.5, 1.5)
لاحظ بعد الرسم أنَّ الشكل قد تعرض إلى تكبير.
6) أقوم بضرب إحداثيات الشكل الأصلي ب 0.5 لتنتج صورة إحداثياتها :
A'(-2,1), B'(0 , 2.5) , C'(2,1) , D'(1,-2) , E'(-1,-2)
لاحظ بعد الرسم أنَّ الشكل قد تعرض إلى تصغير .
7) أرسم الشكل الأصلي ، ثم أقوم بضرب إحداثيات الشكل الأصلي ب لتنتج صورة إحداثياتها :
B'(-1,-2) , C'(-2,3) , D'(0,1)
لاحظ بعد الرسم أنَّ الشكل قد تعرض إلى تصغير.
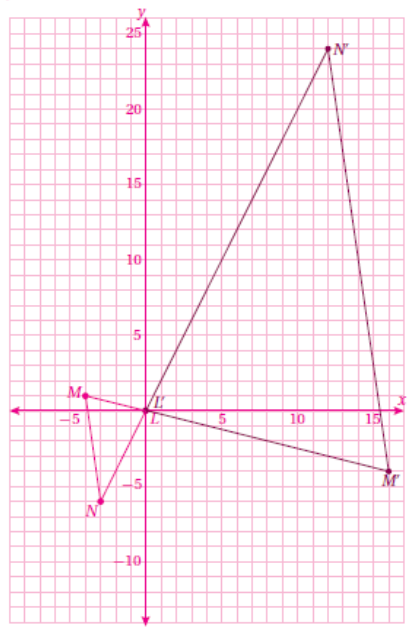
8) أرسم الشكل الأصلي ، ثم أقوم بضرب إحداثيات الشكل الأصلي ب لتنتج صورة إحداثياتها
L'(0,0), M'(16,-4), N'(12,24)
لاحظ بعد الرسم أنَّ الشكل قد تعرض إلى تكبير ، وتعرض إلى دوران بمقدار .
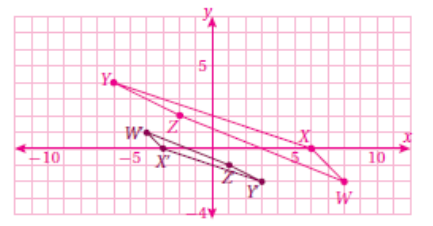
9) أرسم الشكل الأصلي ، ثم أقوم بضرب إحداثيات الشكل الأصلي ب لتنتج صورة إحداثياتها
W'(-4,1), X'(-3,0), Y'(3,-2), Z'(1, -1)
لاحظ بعد الرسم أنَّ الشكل قد تعرض إلى تصغير ، وتعرض إلى دوران بمقدار .
10) أرسم الشكل الأصلي ، ثم أقوم بضرب إحداثيات الشكل الأصلي ب
X'(-7/2 ,7) , Y'(7, 7/2) , Z'(-7/2 , -21/2 )
لاحظ بعد الرسم أنَّ الشكل قد تعرض إلى تكبير .
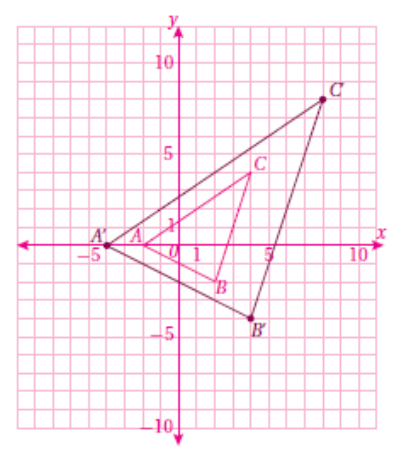
11) اكتشف الخطأ: في الحل الآتي , أوجد سمير معامل التمدد الذي يجعل المثلث الأخضر صورة للمثلث الأزرق تحت تأثير تمدد مركزه نقطة الأصل . اكتشفُ الخطأ في حله , وأصححه.
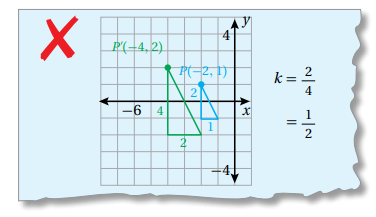 الحل :
الحل :
الخطأ أنه حسب نسبة طول أحد أضلاع الشكل االأصلي إلى طول الضلع المناظر له في الصورة . الصحيح هو العكس
فيكون الجواب : 2 = 4/2
12) تحدٍ : المثلث المبين في الشكل الآتي هو صورة لمثلث تحت تأثير تحويلين هندسيين : تمدد معامله 2 ومركزه مقطة الأصل ،ثم انعكاس حول محور y . أجدُ إحداثيات رؤوس المثلث الأصلي ،مبرراً خطوات الحل.
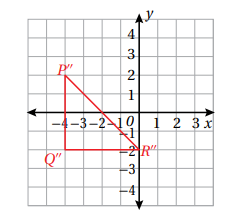 الحل :
الحل :
نقوم بإرجاع إحداثيات الشكل عكسياً حسب ترتيب التحويلات التي حدثت على الشكل .
ففي البداية سنجد إحداثيات الرؤوس قبل الإنعكاس و بعد التمدد وذلك بعكس إحداثيات X :
P′(4, 2),𝑄 ′(4, −2),𝑅 ′(0, −2)
ثم نقسم الإحداثيات على 2 لنجد الرؤوس الأصلية .
الرؤوس الأصلية : 𝑃(2, 1),𝑄(2, −1),𝑅(0, −1)
13) مسألة مفتوحة : أرسم مضلعاً في المستوى الإحداثي ، ثم ارسم تكبيراً وتصغيراً باختيار معامل ومركز تمدد مناسبين.
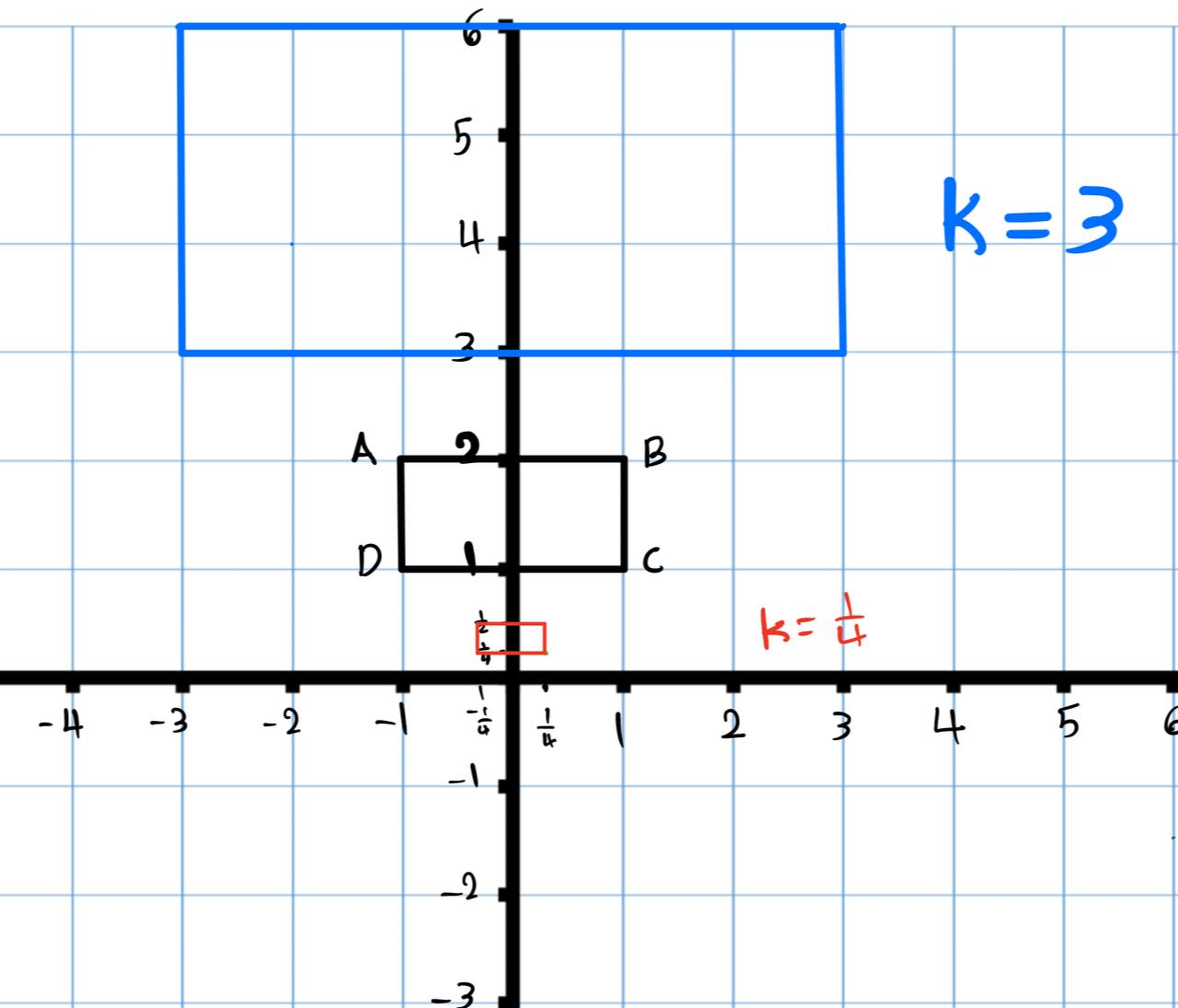
المضلع باللون الأزرق معرض لتكبير معامله 3.
المضلع باللون الأحمر معرض لتصغير معامله 1/4
14) أكتب : كيف أجد صورة لمضلع في المستوى الإحداثي تحت تأثير تمدد مركزه نقطة الأصل ومعامله K ؟
وذلك بضرب إحداثيات النقاط للمضلع المراد تكبيره أو تصغيره بعامل التكبير K .
أسئلة كتاب التمارين :
جد معامل التمدد في كل مما يأتي :
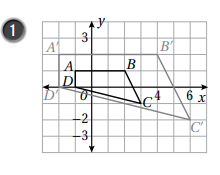 بملاحظة احداثيات الشكل الاصلي والصورة يتضح أن معامل التمدد هو :
بملاحظة احداثيات الشكل الاصلي والصورة يتضح أن معامل التمدد هو :
K=2
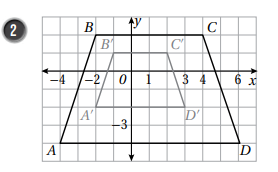 بملاحظة احداثيات الشكل الاصلي والصورة يتضح أن معامل التمدد هو :
بملاحظة احداثيات الشكل الاصلي والصورة يتضح أن معامل التمدد هو :
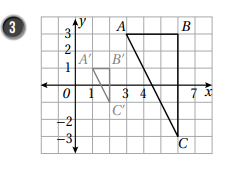
:بملاحظة احداثيات الشكل الاصلي والصورة يتضح أن معامل التمدد هو
أنسخ كل مضلع مما يأتي على ورقة مربعات ثم أرسم صورة له تحت تأثير تمدد مركزه نقطة الأصل ، مستعملاً معامل التمدد المعطى أسفله :
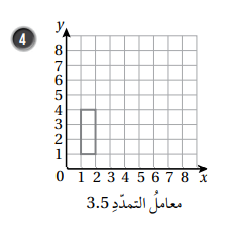
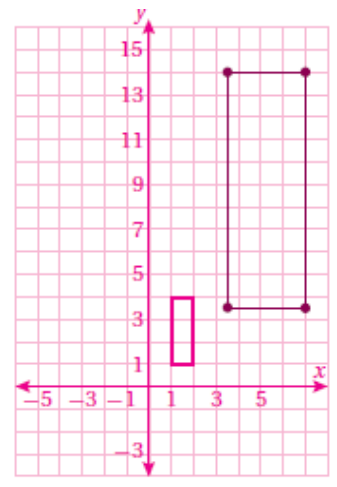
نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب 3.5 ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
(3.5, 3.5), (3.5, 14), (7, 3.5), (7, 14)
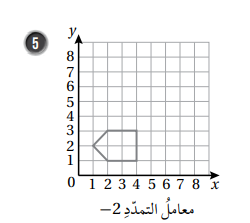
نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب 2- ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
(−2, −4), (−4, −2), (−8, −2), (−8, −6), (−4, −6)
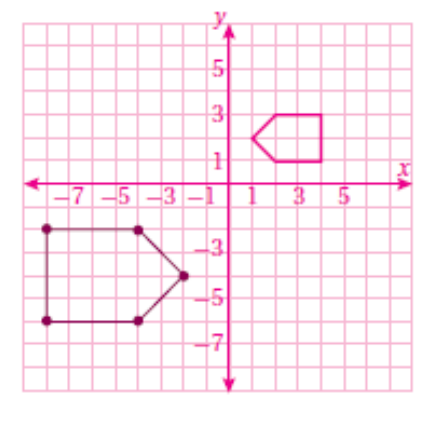
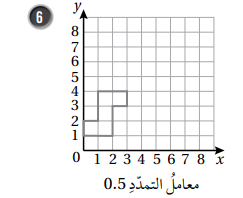
نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب 0.5 ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
(0, 0.5), (0, 1), (0.5, 1), (0.5, 2)
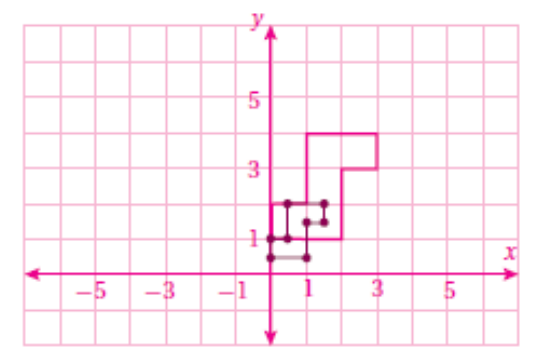
نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب 0.5- ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
𝐷 ′ (2.5, −2), 𝐸 ′ (−1.5, −1), 𝐹 ′ (−2.5, 1.5), 𝐺 ′ (1.5, 2)
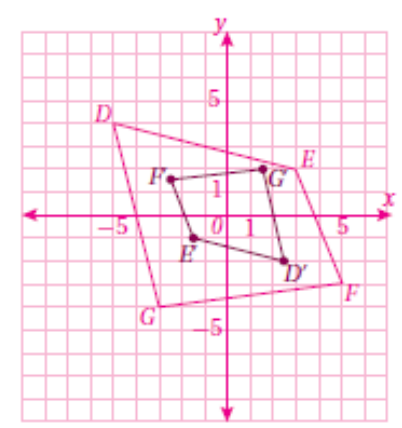
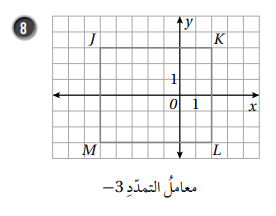
نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب 3 - ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
J′ (15, −9), 𝐾 ′ (−6, −9), 𝐿 ′ (−6, 9) , M ′ (15, 9)
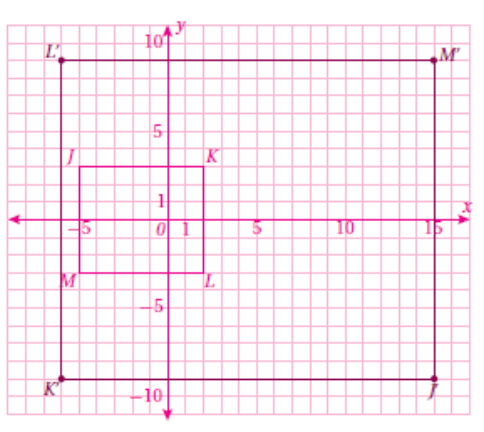
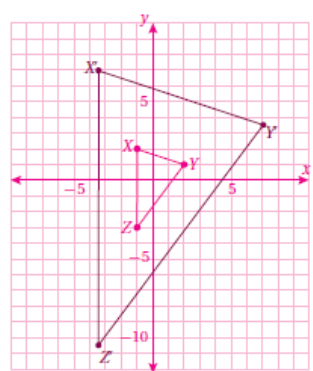
9)
أمثل المضلع المعطاة إحداثيات رؤوسه بيانياً ، ثم أمثل صورته الناتجة عن تمدد مركزه نقطة الأصل ومعامله العدد k المحدد في كل من المسألتين الآتيتين :
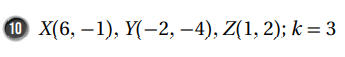
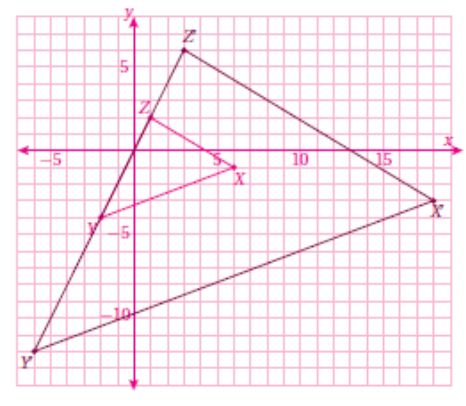
نمثل الشكل الأصلي حسب الإحداثيات المعطاة
ثم نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب 3 ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
X ′(18, −3), 𝑌 ′ (−6, −12), 𝑍 (6, 3)
نلاحظ أن الشكل قد تعرض للتكبير وذلك لأن معامل التكبير أكبر من 1 .
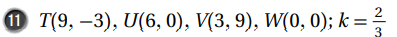
نمثل الشكل الأصلي حسب الإحداثيات المعطاة
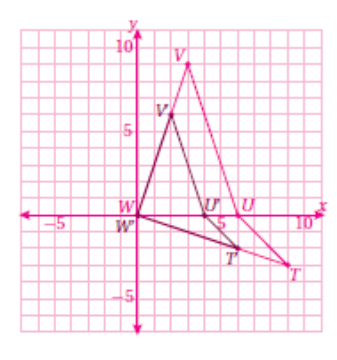
ثم نجد إحداثيات الصورة وذلك بضرب إحداثيات الشكل الاصلي ب ثم نرسم .
وبناءً على ما سبق ستكون إحداثيات الصورة الناتجة :
T ′ (6, −2), 𝑈 ′ (4, 0), 𝑉 ′ (2, 6), 𝑊′ (0, 0)
نلاحظ أن الشكل قد تعرض للتصغير وذلك لأن معامل التكبير أكبر من صفر وأصغر من 1.