رياضيات 9 فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 32

إذا كانَتِ النقطةُ Q هيَ مركزَ $△LMN$ ، وكانَ $NP = 20$ ، فأجدُ كُلًّ ممّا يأتي :  a) طول $\stackrel{—}{NQ}$ b) طول $\stackrel{—}{QP}$

الحل : 

a) طول $\stackrel{—}{NQ}$

$NQ=\frac{2}{3}NP=\frac{2}{3}\left(20\right)=\frac{40}{3}$

 

b) طول $\stackrel{—}{QP}$

نظرية مركز المثلث: $QP+QN=NP$

$QP+\frac{40}{3}=20\to QP=\frac{20}{3}$

---

أتحقق من فهمي صفحة 34

يظهرُ المُثلَّثُ ΔABC في المستوى الإحداثيِّ المُجاوِرِ. أجدُ إحداثييْ مركزِ هذا المُثلَّثِ.

الحل : 

الخطوةُ 1: أجدُ نقطةَ منتصفِ أحدِ أضلاعِ المُثلَّثِ.

أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ AB ولتكنْ K

$K(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\to K(\frac{-2-4}{2},\frac{1+5}{2})\to K(-3,3)$

الخطوةُ 2: أجدُ مركزَ المُثلَّثِ.

•أُعيِّنُ النقطةَ K في المستوى الإحداثيِّ، ثمَّ أرسمُ $CK$ · أُلاحِظُ أنَّ $CK$ أفقية، وأنَّهُ يُمكِنُ إيجادُ طولِها على النحوِ الآتي :  صيغةُ طولِ قطعةٍ مستقيمةٍ أفقية     $CK=|x_2-x_1|$ بالتعويضِ $x_2=-3,x_1=0$      $CK=|-3-0|$ بالتبسيطِ، وإيجادِ القيمةِ المُطلَقةِ     $CK=3$

إذنْ، طولُ $CK$ هوَ 3 وحداتٍ.

 • أفترضُ أنَّ النقطةَ P هيَ مركزُ  ΔABC . ومنْ ثَمَّ ، فإنَّ $CP=\frac{2}{3}CK$؛ لذا يقعُ المركزُ على بُعْدِ  $\frac{2}{3}\left(3\right) = 2$ وحدةٍ إلى يسار الرأسِ C 

 إذنْ، إحداثيّا مركزِ هذا المُثلَّثِ (إحداثيّا النقطةِ P) هما: $(-2 , 3)$

---

أتحقق من فهمي صفحة 36

إذا كانَتْ:$A(-5,-1),B(-2,4),C(3,-1)$ ، فأجدُ إحداثييْ ملتقى ارتفاعاتِ رؤوسِ $△ABC$

الحل: 

الخطوةُ 1: أُمثِّلُ ΔABC بيانيًّا.

الخطوةُ 2: أجدُ ميليْ ضلعينِ منْ أضلاعِ المُثلَّثِ.

$m_{\stackrel{—}{AB}}=\frac{4-(-1)}{-2-(-5)}=\frac{5}{3}$

$m_{\stackrel{—}{AC}}=\frac{-1-4}{3-(-2)}=-1$

الخطوةُ 3: أجدُ معادلةَ الارتفاعِ العموديِّ على كلٍّ منَ الضلعينِ اللذينِ اخترْتُهُما في الخطوةِ السابقةِ.

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{AB}$

صيغةُ الميلِ ونقطةٍ	$y-y_1=m(x-x_1)$
بالتعويضِ $(x_1, y_1)=(3,-1),m=-\frac{3}{5}$	$y+3=-\frac{3}{5}(x-3)$
بالتبسيطِ، وإعادةِ ترتيبِ المعادلةِ	$5y=-3x-6$

تذكر : الرأسُ C هوَ الرأسُ المُقابِلُ ل AB ؛ لذا يقعُ على الارتفاعِ العموديِّ على AB 
· ميلُ الارتفاعِ العموديِّ على AB يساوي سالبَ مقلوبِ ميلِ AB ؛ أيْ إنَّهُ يساوي $-\frac{3}{5}$

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{AC}$

صيغةُ الميلِ ونقطةٍ	$y - y_{1 }= m(x - x_1)$
بالتعويضِ $(x_1, y_1)=(-5,-1),m=1$	$y +1= 1(x + 5)$
بالتبسيطِ، وإعادةِ ترتيبِ المعادلةِ	$y = x + 4$

تذكر  : الرأسُ B هوَ الرأسُ المُقابِلُ ل AC ؛ لذا يقعُ على الارتفاعِ العموديِّ على AC 

· ميلُ الارتفاعِ العموديِّ على AC يساوي سالبَ مقلوبِ ميلِ AC ؛ أيْ إنَّهُ يساوي $-1$

 

الخطوةُ 4 : أحُلُّ نظامَ المعادلتينِ الناتجَ لإيجادِ إحداثييْ ملتقى الارتفاعاتِ. 

المعادلةُ الأولى	$5y=-3x-6$
بالتعويضِ عن y بـ (4 + x)	$5(x+4)=-3x-6$
بالتبسيط	$5x+20=-3x-6$
بحل المعادلة	$x=-3.25$

بما أنَّ x = - 3.25 ، فإنَّ y = 0.75 ، وذلكَ بتعويضِ قيمةِ x في أيٍّ منَ المعادلتينِ.

إذنْ، إحداثيّا ملتقى ارتفاعاتِ رؤوسِ ΔABC هما : (0.75 , 3.25-).

---

أسئلة أتدرب وأحل المسائل

إذا كانَتِ النقطةُ $W$ هي مركز $△QRS$، وكان $RX=48, QW=30$، فأجدُ كُلًّ ممّا يأتي:

$\mathbf{1}\mathbf{)} RW \mathbf{ }\mathbf{2}\mathbf{)} WX \mathbf{3}\mathbf{)} QZ \mathbf{4}\mathbf{)} WZ$

الحل : 

1) $RW =\frac{2}{3} RX=\frac{2}{3}\left(48\right)=32$

---

2) $RX=RW+WX$

$48=32+WX\Rightarrow WX=16$

---

3) $QW=\frac{2}{3}QZ$

$30=\frac{2}{3}QZ\Rightarrow QZ=45$

---

4) $QZ=QW+WZ$

$45=30+WZ\Rightarrow WZ=15$

---

أجدُ كُلًّ ممّا يأتي :

$\mathbf{5}\mathbf{)} PZ \mathbf{ }\mathbf{ }\mathbf{6}\mathbf{)} PX \mathbf{7}\mathbf{)} QZ \mathbf{ }\mathbf{8}\mathbf{)} YZ$

الحل: 

5) $PZ=2ZX=2\left(27\right)=54$

---

6) $PX=PZ+ZX=54+27=81$

---

7) أجد قيمة n

$PZ=2n+17$

$54=2n+17\Rightarrow n=18.5$

$QZ=4n-26=4(18.5)-26=48$

---

8) $YZ=\frac{1}{2}QZ=\frac{1}{2}\left(48\right)=24$

---

9) يظهرُ المُثلَّثُ $△ABC$في المستوى الإحداثيِّ المُجاوِرِ.

أجدُ إحداثييْ مركزِ هذا المُثلَّثِ.

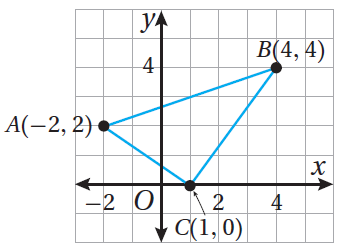
الحل: 

الخطوةُ 1: أجدُ نقطةَ منتصفِ أحدِ أضلاعِ المُثلَّثِ.

أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ AB ولتكنْ M

$M(\frac{x_1+ x_2}{2},\frac{y_1+y_2}{2})$

$M(\frac{4+(-2)}{2},\frac{4+2}{2})\to M(1 , 3)$

 

الخطوةُ 2 : أجدُ مركزَ المُثلَّثِ.

• أُعيِّنُ النقطةَ M في المستوى الإحداثيِّ، ثمَّ أرسمُ CM

أجد طول CM 

صيغةُ طولِ قطعةٍ مستقيمةٍ رأسية 

$CM=|y_2-y_1|=|3 - 0|=3$

• أفترضُ أنَّ النقطةَ P هيَ مركزُ  ΔABC . ومنْ ثَمَّ ، فإنَّ $CP = \frac{2}{3}CM$ ؛ لذا يقعُ المركزُ على بُعْدِ $\frac{2}{3}\left(3\right) = 2$  وحدةٍ أعلى الرأسِ C 

 إذنْ، إحداثيّا مركزِ هذا المُثلَّثِ (إحداثيّا النقطةِ P) هما : (2 ، 1)

---

أجدُ إحداثييْ مركزِ المُثلَّثِ المعطاةِ إحداثياتُ رؤوسِهِ في كلٍّ ممّا يأتي :  

$\mathbf{10}\mathbf{)}\mathbf{ }F(1,5),G(-2,7), H(-6,3)$

الخطوةُ 1 : أرسم المثلث في المستوى الإحداثي ، ثمّ أجدُ نقطةَ منتصفِ أحدِ أضلاعِ المُثلَّثِ.

أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ HG ولتكنْ N

$N(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\to N(\frac{-6-2 }{2},\frac{3+7}{2})\to N(-4,5)$

الخطوةُ 2 : أجدُ مركزَ المُثلَّثِ.

• أُعيِّنُ النقطةَ N في المستوى الإحداثيِّ، ثمَّ أرسمُ FN أجد طول FN صيغةُ طولِ قطعةٍ مستقيمةٍ أفقية :  $FN=|x_2-x_1|=|-4-1|=5$ • أفترضُ أنَّ النقطةَ P هيَ مركزُ  ΔFGH . ومنْ ثَمَّ ، فإنَّ $FP=\frac{2}{3}FN$  ؛ لذا يقعُ المركزُ على بُعْدِ  $\frac{2}{3}\left(5\right)=\frac{10}{3}\approx 3.3$ وحدةٍ إلى يسار الرأسِ F  إذنْ، إحداثيّا مركزِ هذا المُثلَّثِ (إحداثيّا النقطةِ P) هما: $(-3.3,5)$

 

---

$\mathbf{11}\mathbf{)} A(5,5),B(11,-3),C(-1,1)$

الخطوةُ 1 : أرسم المثلث في المستوى الإحداثي، ثمّ أجدُ نقطةَ منتصفِ أحدِ أضلاعِ المُثلَّثِ.

أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ AB  ولتكنْ R

$R(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\to R(\frac{5+11}{2},\frac{5-3}{2})\to R(8,1)$

الخطوةُ 2 : أجدُ مركزَ المُثلَّثِ.

• أُعيِّنُ النقطةَ R في المستوى الإحداثيِّ، ثمَّ أرسمُ  RC أجد طول  RC صيغةُ طولِ قطعةٍ مستقيمةٍ أفقية :  $RC=|x_2-x_1|=|8-(-1\left)\right|=9$ • أفترضُ أنَّ النقطةَ H هيَ مركزُ  ΔABC . ومنْ ثَمَّ ، فإنَّ $CH=\frac{2}{3}CR$؛ لذا يقعُ المركزُ على بُعْدِ $\frac{2}{3}\left(9\right)=6$ وحدةٍ إلى يمين الرأسِ C إذنْ، إحداثيّا مركزِ هذا المُثلَّثِ (إحداثيّا النقطةِ H) هما: $(5,1)$

---

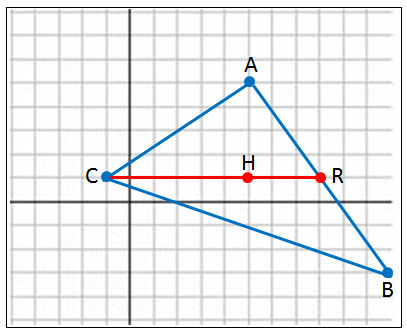يظهرُ $△ABC$و $△GFH$ في الشكلِ المُجاوِرِ. أُحدِّدُ إذا كانَتْ كلُّ قطعةٍ مستقيمةٍ في ما يأتي تُمثِّلُ ارتفاعًا، أوْ عمودًا مُنصِّفًا، أوْ قطعةً مُتوسِّطةً، أوْ مُنصِّفَ زاويةٍ:

$\mathbf{12}\mathbf{)} BD \mathbf{ }\mathbf{13}\mathbf{)}\mathbf{ }FJ \mathbf{14}\mathbf{)} CE \mathbf{ }\mathbf{15}\mathbf{)} KL$

الحل : 

12) $BD$: مُنصف الزاوية CBA

13) $FJ$: قطعة متوسطة .

14) $CE$: ارتفاع .

15) $KL$: عمودًا مُنصفًا . 

---

أجدُ إحداثييْ ملتقى ارتفاعاتِ المُثلَّثِ المعطاةِ إحداثياتُ رؤوسِهِ في كلٍّ ممّا يأتي:  

$\mathbf{16}\mathbf{)} X(-2,-2),Y(6,10),Z(6,6)$

الخطوةُ 1 : أُمثِّلُ ΔXYZ بيانيًّا. الخطوةُ 2 : أجدُ ميليْ ضلعينِ منْ أضلاعِ المُثلَّثِ. $m_{\stackrel{—}{XY}}=\frac{10-(-2)}{6-(-2)}=\frac{3}{2}$ $m_{\stackrel{—}{XZ}}=\frac{6-(-2)}{6-(-2)}=1$

الخطوةُ 3 : أجدُ معادلةَ الارتفاعِ العموديِّ على كلٍّ منَ الضلعينِ اللذينِ اخترْتُهُما في الخطوةِ السابقةِ.

• معادلةُ الارتفاعِ العموديِّ على $\overline{XY}$

صيغة الميل ونقطة	$y - y_{1 }= m(x - x_1)$
بتعويض $(x_1, y_1)=(6,6),m=-\frac{2}{3}$	$y-6=-\frac{2}{3}(x-6)$
بالتبسيط	$y=-\frac{2}{3}x+10$
بضرب المعادلة في 3 للتخلص من الكسر	$3y=-2x+30$

 

تذكر  : الرأسُ Z هوَ الرأسُ المُقابِلُ لـ XY ؛ لذا يقعُ على الارتفاعِ العموديِّ على XY 
· ميلُ الارتفاعِ العموديِّ على XY يساوي سالبَ مقلوبِ ميلِ XY ؛ أيْ إنَّهُ يساوي $-\frac{2}{3}$ 

• معادلةُ الارتفاعِ العموديِّ على $\overline{XZ}$

صيغة الميل ونقطة	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(6,10) ,m=-1$	$y-10=-1(x-6)$
بالتبسيط وإعادة ترتيب المعادلة	$y=-x+16$

 

تذكر  : الرأسُ Y هوَ الرأسُ المُقابِلُ لـ XZ ؛ لذا يقعُ على الارتفاعِ العموديِّ على XZ 
· ميلُ الارتفاعِ العموديِّ على XZ يساوي سالبَ مقلوبِ ميلِ XZ ؛ أيْ إنَّهُ يساوي $-1$

 

الخطوةُ 4 : أحُلُّ نظامَ المعادلتينِ الناتجَ لإيجادِ إحداثييْ ملتقى الارتفاعاتِ.

المعادلة الأولى	$3y=-2x+30$
بالتعويض بدلًا من y  بـ  $(-x+16)$	$-x+16=-\frac{2}{3}x+10$
بحل المعادلة	$x=18$

بما أنَّ x =18 ، فإنَّ y = -2 ، وذلكَ بتعويضِ قيمةِ x في أيٍّ منَ المعادلتينِ.

إذنْ، إحداثيّا ملتقى ارتفاعاتِ رؤوسِ ΔXYZ هما:$(18,-2)$.

---

$\mathbf{17}\mathbf{)} A(4,-3),B(8,5),C(8,-8)$

الخطوةُ 1 : أُمثِّلُ ΔABC بيانيًّا. الخطوةُ 2 : أجدُ ميليْ ضلعينِ منْ أضلاعِ المُثلَّثِ. $m_{\stackrel{—}{AB}}=\frac{5-(-3)}{8-4}=2$ $m_{\stackrel{—}{AC}}=\frac{-8-(-3)}{8 - 4}=-\frac{5}{4}$

 

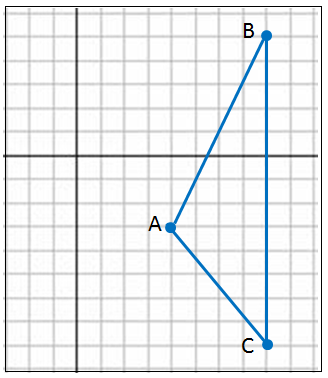الخطوةُ 3 : أجدُ معادلةَ الارتفاعِ العموديِّ على كلٍّ منَ الضلعينِ اللذينِ اخترْتُهُما في الخطوةِ السابقةِ.

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{AB}$

صيغة الميل ونقطة	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(8,-8),m=-\frac{1}{2}$	$y+8=-\frac{1}{2}(x-8)$
بالتبسيط	$y=-\frac{1}{2}x-4$
بضرب المعادلة في 2 للتخلص من الكسر	$2y=-x-8$

 

تذكر : الرأسُ C هوَ الرأسُ المُقابِلُ لـ AB ؛ لذا يقعُ على الارتفاعِ العموديِّ على AB 
· ميلُ الارتفاعِ العموديِّ على AB يساوي سالبَ مقلوبِ ميلِ AB ؛ أيْ إنَّهُ يساوي $-\frac{1}{2}$

 

• معادلةُ الارتفاعِ العموديِّ على $\overline{AC}$

صيغة الميل ونقطة	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(8,5),m=\frac{4}{5}$	$y-5=\frac{4}{5}(x-8)$
بالتبسيط	$y=\frac{4}{5}x-\frac{7}{5}$
بضرب المعادلة في 5 للتخلص من الكسر	$5y=4x-7$

تذكر  : الرأسُ B هوَ الرأسُ المُقابِلُ لـ AC ؛ لذا يقعُ على الارتفاعِ العموديِّ على AC 
· ميلُ الارتفاعِ العموديِّ على AC يساوي سالبَ مقلوبِ ميلِ AC ؛ أيْ إنَّهُ يساوي $\frac{4}{5}$

الخطوةُ 4 : أحُلُّ نظامَ المعادلتينِ الناتجَ لإيجادِ إحداثييْ ملتقى الارتفاعاتِ.

بحل المعادلتين بالحذف ينتج أنّ x = - 2  ،   y = -3   

إذنْ، إحداثيّا ملتقى ارتفاعاتِ رؤوسِ ΔABC  هما : ( 3- ,  2-). 

---

18) أحُلُّ المسألةَ الواردةَ بدايةَ الدرسِ.

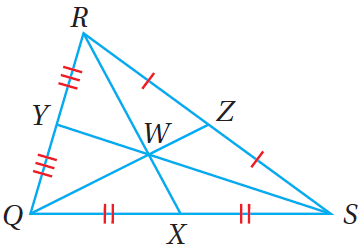
مسألةُ اليومِ: تُمثِّلُ النقطةُ P في الشكلِ المُجاوِرِ موقعَ مستشفى حكوميٍّ في إحدى المحافظاتِ الأردنيةِ، وتُمثِّلُ النقاطُ الأُخرى في الشكلِ عددًا منَ المناطقِ السكنيةِ القريبةِ منْهُ. إذا كانَ بُعْدُ المنطقةِ S عنِ المنطقةِ Z هوَ 8Km، فما بُعْدُ المستشفى عنِ المنطقةِ Z؟

الحل: 

$PZ=\frac{2}{3}SZ=\frac{2}{3}\left(8\right)=\frac{16}{3}\approx 5.3Km$

---

مهاراتُ التفكيرِ العليا

19) أكتشفُ الخطأَ: يُمثِّلُ الشكلُ المُجاوِرُ حَلَّ خالدٍ لإيجادِ طولِ DE في $△ABC$، حيث D مركز المثلث. 

أكتشفُ الخطأَ في حَلِّ خالدٍ، ثمَّ أُصحِّحُهُ.

الحل: 

أخطأ خالد باستخدام النسبة  $\frac{2}{3}$ حيث المطلوب طول القطعة المستقيمة DE الواصلة بين مركز المثلث ومنتصف الضلع BC

والصحيح أنّ DE تُمثل $\frac{1}{3}$ القطعة المستقيمة AE الواصلة بين الرأس A ومنتصف الضلع المقابل للرأس .

$DE=\frac{1}{3}AE=\frac{1}{3}\left(12\right)=4$

---

20) تبريرٌ : يظهرُ في المستوى الإحداثيِّ المُجاوِرِ ΔABC الذي مركزُهُ النقطةُ P إذا حُرِّكَتِ النقطةُ B إلى اليمينِ على المحورِ x ، وظلَّتْ كلٌّ منَ النقطةِ A والنقطةِ C في موقعِها، فما تأثيرُ ذلكَ في موقعِ كلٍّ منْ مركزِ ΔABC وملتقى ارتفاعاتِهِ؟ أُبرِّرُ إجابتي.

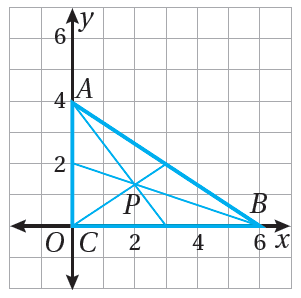
الحل: 

• إذا حُرِّكَتِ النقطةُ B إلى اليمينِ على المحورِ x ، وظلَّتْ كلٌّ منَ النقطةِ A والنقطةِ C في موقعِها، فإنّ الإحداثي x لمركز المثلث (P) سيتحرك إلى اليمين مع بقاء الإحداثي y ثابتًا .

• ملتقى ارتفاعات المثلث سيبقى ثابتًا في رأس القائمة .

---

تحدٍّ : يُبيِّنُ الشكلُ المُجاوِرُ ΔJKL . أستعملُ المعلوماتِ المعطاةَ في الشكلِ

للإجابةِ عنِ السؤالينِ الآتيينِ:

 

21) أجدُ مساحةَ كلٍّ منَ ΔJKM ، و ΔKML بدلالةِ h، مُقارِنًا بينَ مساحتيِ المُثلَّثينِ.

22) في السؤالِ السابقِ، هلْ تختلفُ العلاقةُ بينَ مساحتيِ المُثلَّثينِ الناتجينِ منَ القطعةِ المُتوسِّطةِ للمُثلَّثِ تبعًا لاختلافِ نوعِ المُثلَّثِ، مُبرِّرًا إجابتي؟

الحل : 

21) مساحةَ كلٍّ منَ ΔJKM ، و ΔKML بدلالةِ h 

مساحة ΔJKM 

$A_1=\frac{1}{2}JM\times h=\frac{1}{2}\left(9\right)\times h=\frac{9}{2}h$

مساحة ΔKML 

$A_2=\frac{1}{2}LM\times h=\frac{1}{2}\left(9\right)\times h=\frac{9}{2}h$

المثلثين لهما نفس المساحة . 

22) لا تختلفُ العلاقةُ بينَ مساحتيِ المُثلَّثينِ الناتجينِ منَ  القطعةِ المُتوسِّطةِ للمُثلَّثِ تبعًا لاختلافِ نوعِ المُثلَّثِ؛ لأنّ لهما قاعدتين متساويتين ولهما نفس الارتفاع .  

---

أسئلة كتاب التمارين   

أُحدِّدُ مركزَ كلِّ مُثلَّثٍ ممّا يأتي : 

الحل : مركز المثلث النقطة H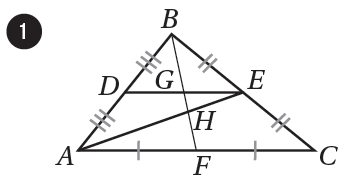
الحل : مركز المثلث النقطة M

---

إذا كانَتِ النقطةُ B هيَ مركزَ $△HJK$، وكان: $HD=21, BK=18$ ، فأجدُ قياسَ كلٍّ ممّا يأتي:

$\mathbf{3}\mathbf{)} HB \mathbf{4}\mathbf{)}\mathbf{ }BD \mathbf{5}\mathbf{)} CK \mathbf{6}\mathbf{)} CB$

الحل: 

3) $HB=\frac{2}{3}HD=\frac{2}{3}\left(21\right)=14$

---

4) $HD=HB+BD$

$21=14+BD\Rightarrow BD=7$

---

5) $BK=\frac{2}{3}CK$

$18=\frac{2}{3}CK\Rightarrow CK=27$

---

6) $CK=BK+CB$

$27=18+CB\Rightarrow CB=9$

---

أجدُ قياسَ كلٍّ ممّا يأتي:

$\mathbf{7}\mathbf{)} BP \mathbf{ }\mathbf{8}\mathbf{)}\mathbf{ }BD \mathbf{9}\mathbf{)} CP \mathbf{ }\mathbf{10}\mathbf{)} PE$

الحل: 

7) أجد قيمة x 

$AE=EB$

$x+8=2x-3 \Rightarrow x=11$

$BP=x-1=11-1=10$

---

8) $PB=\frac{2}{3}BD$

$10=\frac{2}{3}BD\Rightarrow BD=15$

---

9) $BD=DP+BP$

$15=DP+10$

$DP=5\Rightarrow y=5$

$CP=3y+3=3\left(5\right)+3=18$

---

10) $PE=y+4=5+4=9$

---

11) يظهرُ المُثلَّثُ ΔABC في المستوى الإحداثيِّ المُجاوِرِ.

أجدُ إحداثييْ مركزِ هذا المُثلَّثِ.

الحل : 

أجدُ نقطةَ منتصفِ ضلعين في المُثلَّثِ. أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ AB  ولتكنْ F $F(\frac{-1+6 }{2},\frac{-1+6}{2})\to F(2.5,2.5)$  • أُعيِّنُ النقطةَ F في المستوى الإحداثيِّ، ثمَّ أرسمُ CF أستعملُ صيغةَ نقطةِ المنتصفِ لإيجادِ منتصفِ BC  ولتكنْ G $G(\frac{6+6 }{2},\frac{2+6}{2})\to G(6,4)$ • أُعيِّنُ النقطةَ G في المستوى الإحداثيِّ، ثمَّ أرسمُ AG

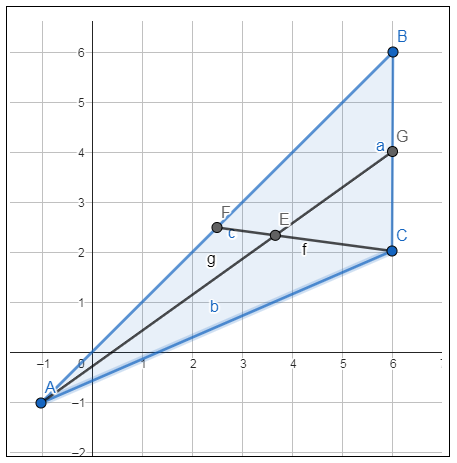 نقطة التقاء القطعتين المتوسطتين هي مركز المثلث $E(3.7,2.3)$ (بالتقريب).

---

أجدُ إحداثييْ ملتقى ارتفاعاتِ المُثلَّثِ المعطاةِ إحداثياتُ رؤوسِهِ في كلٍّ ممّا يأتي: 

$\mathbf{12}\mathbf{)} X(2,-2),Y(4,6),Z(8,-2)$

الخطوةُ 1 : أُمثِّلُ ΔXYZ بيانيًّا. الخطوةُ 2 : أجدُ ميليْ ضلعينِ منْ أضلاعِ المُثلَّثِ. $m_{\stackrel{—}{XY}}=\frac{4-(-2)}{6 -2}=\frac{3}{2}$ $m_{\stackrel{—}{YZ}}=\frac{-2 - 4}{8-6}=-3$

 

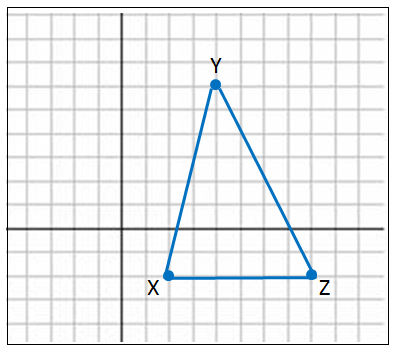الخطوةُ 3 : أجدُ معادلةَ الارتفاعِ العموديِّ على كلٍّ منَ الضلعينِ اللذينِ اخترْتُهُما في الخطوةِ السابقةِ.

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{XY}$

صيغةُ الميلِ ونقطةٍ	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(8,-2),m=-\frac{2}{3}$	$y+2=-\frac{2}{3}(x-8)$
بالتبسيط	$y=-\frac{2}{3}x+\frac{10}{3}$
بضرب المعادلة في 3 للتخلص من الكسر	$3y=-2x+10$

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{YZ}$

صيغةُ الميلِ ونقطةٍ	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(2,-2),m=\frac{1}{3}$	$y+2=\frac{1}{3}(x-2)$
بالتبسيط	$y=\frac{1}{3}x-\frac{8}{3}$
بضرب المعادلة في 3 للتخلص من الكسر	$3y=x-8$

بحل المعادلتين بالتعويض ينتج أنّ x = 6، وبتعويض قيمة x في إخدى المعادلتين فإنّ $y=-\frac{2}{3}$

إذنْ، إحداثيّا ملتقى ارتفاعاتِ رؤوسِ ΔXYZ هما:$(6,-\frac{2}{3})$

---

$\mathbf{13}\mathbf{)} A(-5,8),B(4,5),C(-2,5)$

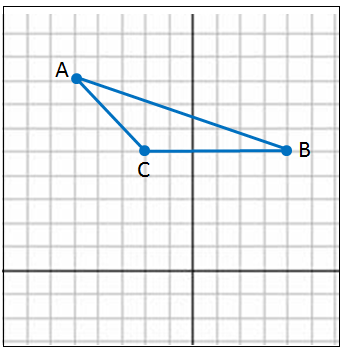
الخطوةُ 1: أُمثِّلُ ΔABC بيانيًّا. الخطوةُ 2: أجدُ ميليْ ضلعينِ منْ أضلاعِ المُثلَّثِ. $m_{\stackrel{—}{AB}}=\frac{8-5}{-5 -4}=-\frac{1}{3}$ $m_{\stackrel{—}{AC}}=\frac{8-5}{-5 -(-2)}=-1$

الخطوةُ 3 : أجدُ معادلةَ الارتفاعِ العموديِّ على كلٍّ منَ الضلعينِ اللذينِ اخترْتُهُما في الخطوةِ السابقةِ.

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{AB}$ 

صيغةُ الميلِ ونقطةٍ	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(-2,5),m=3$	$y-5=3(x+2)$
بالتبسيط	$y = 3x + 11$

 

• معادلةُ الارتفاعِ العموديِّ على $\stackrel{—}{AC}$

صيغةُ الميلِ ونقطةٍ	$y-y_1=m(x-x_1)$
بتعويض $(x_1, y_1)=(4,5),m=1$	$y - 5= 1(x - 4)$
بالتبسيط	$y=x+1$

بحل المعادلتين بالتعويض ينتج أنّ x =  -5 ، وبتعويض قيمة x في إخدى المعادلتين فإنّ y = -4

إذنْ، إحداثيّا ملتقى ارتفاعاتِ رؤوسِ ΔABC هما : $(-5,-4)$

---