أولًا : أيجاد المشتقة باستخدام التعريف العام
تعلّمت سابقًا أنّه يُمكن إيجاد ميل منحنى الاقتران عند نقطة ما عن طريق المشتقة، وذلك بإيجاد ميل المماس عند هذه النقطة.
|
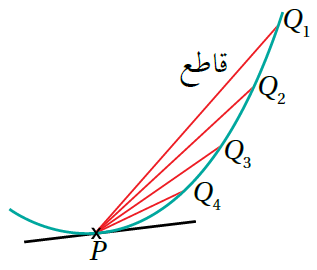
يُمثّل الشكل المجاور مماسًا لمنحنى اقتران عند النقطة P . أُلاحِظ أنَّ النقطة Q1 في أثناء حركتها على منحنى الاقتران نحو النقطة P تمرّ بالنقاط : Q2 و Q3 و Q4 ، وأنّ ميل كل من القواطع : يقترب شيئًا فشيئًا من ميل المماس عند النقطة P
|
 |
اعتمادًا على ذلك ، يُمكِن إيجاد مشتقة اقتران قاعدته معلومة ، مثل :
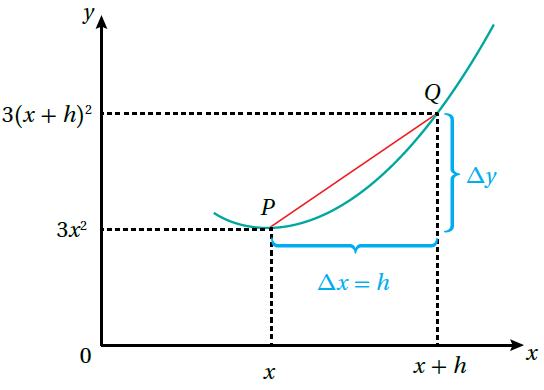
فمثاً، إذا كانت النقطة Q تبعد مسافة أفقية صغيرة مقدارها h عن النقطة ، فإنَّ إحداثيي النقطة Q هما : (إذن: ميل القاطع PQ يساوي :
 |
|
وعند اقتراب النقطة Q من النقطة P ، فإنَّ المسافة الأفقية h تصبح أصغر فأصغر ؛ ما يعني أنّ هذه المسافة تقترب من الصفر ، وهي تُكتَب كما يأتي: .h → 0 وبذلك ، فإنَّ ميل المماس عند النقطة P يساوي نهاية 6x + 3h عندما h → 0 :
وتُسمى 6x مشتقة الاقتران ، ويُرمَز إليها بالرمز
إذن : إذا كان فإنّ : .
يُطلَق على هذه الطريقة في إيجاد مشتقة اقتران عند نقطة ما اسم التعريف العام للمشتقة ( definition of the derivative )
ملاحظة : (يُرمز إلى مشتقة الاقتران : ، بالرموز : ، ، )
مفهوم أساسي ( التعريف العام للمشتقة)
مشتقة الاقتران f بالنسبة إلى المُتغيِّر x هي الاقتران ' f الذي قيمته عند x :
، بشرط وجود النهاية.
مثال :
أجد مشتقة الاقتران : باستخدام التعريف العام للمشتقة عندما
االحل :
| التعريف العام للمشتقة | |
| بتعويض | |
| بتعويض | |
| بالتبسيط | |
| بإخراج h عامل مشترك واختصاره من البسط والمقام | |
| بتعويض |
يُمكن استعمال التعريف العام للمشتقة لإيجاد اقتران جديد يُمثل مشتقة الاقتران الأصلي.
مثال :
أجد مشتقة الاقتران: y = 6x - 5 باستخدام التعريف العام للمشتقة.
الحل :
| التعريف العام للمشتقة | |
| بتعويض | |
| بفك الاقواس والتبسيط | |
| باختصار h من البسط والمقام | |
| نهاية الثابت |
ثانيًا : أيجاد المشتقة باستخدام قواعد الاشتقاق
1) مشتقة اقتران القوة
يُطلق على الاقتران : الذي فيه n عدد حقيقي اسم اقتران القوَّة ( power function )، ومن أمثلته :
يُمكن اشتقاق اقترانات القوة باستخدام قاعدة مشتقة اقتران القوة.
مفهوم أساسي (مشتقة اقترانات القوة)
بالكلمات : عند اشتقاق الاقتران : ، فإنَّ أُسّ x في المشتقة يكون أقل بواحد من أُسّ x في الاقتران الأصلي ، ومعامل x في المشتقة يساوي أُسّ x في الاقتران الأصلي.
بالرموز : إذا كان ، حيث n عدد حقيقي ، فإنّ :
مثال :
أجد مشتقة كل اقتران في كل مما يأتي :
|
الحل : |
|
|
قاعدة مشتقة القوة |
|
| الحل : | |
| كتابة الاقتران في صورة أُسّية | |
| قاعدة مشتقة القوة | |
| التبسيط | |
| تعريف الأس السالب | |
| الحل : | |
| تحويل الصيغة الجذرية إلى صيغة أسية | |
| قاعدة مشتقة القوة | |
| التبسيط | |
| تحويل الصيغة الأسية إلى الصيغة الجذرية |
توجد أيضًا بعض القواعد التي تُسهِّل عملية إيجاد مشتقة الاقترانات التي تتضمَّن حدودها اقترانات القوة.
مفهوم أساسي (قواعد أخرى للمشتقة)
مشتقة الثابت :
إذا كان y = c ، حيث c عدد حقيقي ، فإنّ : ، أي أنّ مشتقة الثابت تساوي صفرًا.
مشتقة مضاعفات القوة :
إذا كان ، حيث n و a عددان حقيقيان ، فإنّ : .
مشتقة المجموع أو الفرق :
إذا كان y = u ± v ، حيث u و v اقترانا قوة ، فإنّ : .
مثال :
أجد مشتقة كل اقتران في كل مما يأتي :
| الحل : | |
| تحويل الصيغة الجذرية إلى صيغة أسية | |
| قاعدة مشتقة اقتران القوة، وقاعدة مشتقة المجموع | |
| التبسيط بتحويل الأس السالب إلى موجب وتحويل الصيغة الأسية إلى الصيغة الجذرية | |
| الحل : | |
| بتوزيع البسط على المقام | |
| بالإختصار وكتابة الاقتران في الصيغة الأسية | |
| قواعد مشتقات الثابت ، ومضاعفات القوة ، والفرق | |
| التبسيط |
ثالثًا : أيجاد السرعة اللحظية لجسم متحرك (استخدام قواعد المشتقة)
تَعلَم أنّ : السرعة اللحظية لجسم مُتحرك تساوي مشتقة اقتران المسافة المقطوعة عند لحظة مُعيّنة ، والآن سأستخدم قواعد المشتقة التي تعرّفتها في هذا الدرس لإيجاد السرعة اللحظية.
مثال :
يُمثل الاقتران : المسافة التي يقطعها جسم متحرك بالأمتار (m) ، حيث t الزمن بالثواني (s) ، أجد سرعة الجسم بعد (5) ثوانٍ من بدء حركته.
الحل :
السرعة = مشتقة اقتران المسافة ، والمطلوب إيجاد السرعة عندما t = 5
| مشتقة اقتران المسافة | |
| تعويض t = 5 | |
| بالتبسيط |
إذن سرعة الجسم بعد 5 ثوانٍ من بدء حركته هي 45m/s