رياضيات فصل أول

الثامن

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

تحليلُ ثلاثياتِ الحدود $x^{2} + b x + c$

أتحقق من فهمي 1 : أحلل ما يأتي :

$1) x^{2} + 11 x + 10$

نبحث عن عددين موجبين ناتج ضربهما 10 ومجموعهما 11 .

$x^{2} + 11 x + 10 = (x + 5) (x + 6)$

$2) x^{2} + 9 x + 14$

نبحث عن عددين موجبين ناتج ضربهما14 ومجموعهما 9 .

$x^{2} + 9 x + 14 = (x + 7) (x + 2)$

أتحقق من فهمي 2 : أحلل ما يأتي :

$1) y^{2} - 5 y + 6$

نبحث عن عددين سالبين ناتج ضربهما 6 ومجموعهما 5- .

$y^{2} - 5 y + 6 = (y - 3) (y - 2)$

$2) x^{2} - 11 x + 30$

نبحث عن عددين سالبين ناتج ضربهما 30 ومجموعهما 11-

$x^{2} - 11 x + 30 = (x - 6) (x - 5)$

أتحقق من فهمي 3 : أحلل ما يأتي :

$1) x^{2} + 2 x - 8$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 8- و مجموعهما 2+

$x^{2} + 2 x - 8 = (x + 4) (x - 2)$

$2) x^{2} - x - 42$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 42 - و مجموعهما 2-

$x^{2} - x - 42 = (x - 7) (x + 6)$

يمثلُ ثلاثيُّ الحدودِ $x^{2} - 25 x + 100$ مساحةَ بابٍ مستطيلِ الشكلِ بالمترِ المربعِ. إذا كانَ عرضُ البابِ $(x - 5)$ مترًا، فأجدُ كلًّ مِنْ طولِهِ ومحيطِهِ بدلالةِ x .

الحل :

مساحة الباب = طوله*عرضه .

ومنه :

$A = L * W$

$x^{2} - 25 x + 100 = L * (x - 5)$

$(x - 5) (x - 20) = L * (x - 5)$

$\frac{(x - 5) (x - 20)}{(x - 5)} = \frac{L * (x - 5)}{(x - 5)}$

$x - 20 = L$

الآن نجد المحيط :

$P = 2 l + 2 w$

$= 2 (x - 20) + 2 (x - 5)$

$= 2 ((x - 20) + (x - 5))$

$= 2 (2 x - 25) = 4 x - 50$

أتدرب وأحل المسائل :

أحللُ كلًّ ممّا يأتي:

$1) x^{2} + 2 x - 24$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 24- ومجموعهما 2+ .

$x^{2} + 2 x - 24 = (x - 4) (x + 6)$

$2) y^{2} + 3 y - 10$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 10- ومجموعهما 3+ .

$y^{2} + 3 y - 10 = (y - 2) (y + 5)$

$3) x^{2} + 29 x + 100$

نبحث عن عددين موجبين ناتج ضربهما 100 ومجموعهما 29 .

$x^{2} + 29 x + 100 = (x + 25) (x + 4)$

$4) w^{2} - 6 w + 8$

نبحث عن عددين سالبين ناتج ضربهما 8 ومجموعهما 6- .

$w^{2} - 6 w + 8 = (w - 2) (w - 4)$

$5) - 10 q + q^{2} + 21$

نرتب المسألة أولاً لتصبح : $q^{2} - 10 q + 21$

نبحث عن عددين سالبين ناتج ضربهما 21 ومجموعهما 10 -

$q^{2} - 10 q + 21 = (q - 7) (q - 3)$

$6) y^{2} + 20 y + 100$

نبحث عن عددين موجبين ناتج ضربهما 100 ومجموعهما 20 .

$y^{2} + 20 y + 100 = (y + 10) (y + 10)$

$7) a^{2} + 5 a + 6$

نبحث عن عددين موجبين ناتج ضربهما 6 ومجموعهما 5 .

$a^{2} + 5 a + 6 = (a + 3) (a + 2)$

$8) w^{2} - 9 w - 10$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 10- ومجموعهما 9- .

$w^{2} - 9 w - 10 = (w - 10) (w + 1)$

$9) x^{2} + x - 30$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 30 - ومجموعهما 1+ .

$x^{2} + x - 30 = (x + 6) (x - 5)$

$10) 13 y + 30 + y^{2}$

أولاً نرتب المسألة لتصبح : $y^{2} + 13 y + 30$

نبحث عن عددين موجبين ناتج ضربهما 30 ومجموعهما 13 .

$y^{2} + 13 y + 30 = (y + 3) (y + 10)$

$11) w^{2} + 11 w + 18$

نبحث عن عددين موجبين ناتج ضربهما 18 ومجموعهما 11 .

$w^{2} + 11 w + 18 = (w + 9) (w + 2)$

$12) t^{2} - t - 90$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 90 - ومجموعهما 1- .

$t^{2} - t - 90 = (t - 10) (t + 9)$

$13) f^{2} + 22 f + 21$

نبحث عن عددين موجبين ناتج ضربهما 21 ومجموعهما 22 .

$f^{2} + 22 f + 21 = (f + 21) (f + 1)$

$14) h^{2} - h - 72$

نبحث عن عددين مختلفين في الإشارة ناتج ضربهما 72 - ومجموعهما 1- .

$h^{2} - h - 72 = (h - 9) (h + 8)$

$15) m^{2} - 18 m + 81$

نبحث عن عددين سالبين ناتج ضربهما 81 ومجموعهما 18 -

$m^{2} - 18 m + 81 = (m - 9) (m - 9)$

يمثلُّ كلُّ ثلاثيِّ حدودٍ ممّا يأتي مساحةَ مستطيلٍ بالمترِ المربعِ. أجدُ مقدارَينِ جبريَّينِ
يمثلانِ طولً وعرضًا ممكنَينِ لكلِّ مستطيلٍ.

ملاحظة مساعدة للحل : لإيجاد الطول والعرض للمساحات المعطاة ، نحلل المقادير فقط بحيث نحصل على حاصل ضرب مقادرين أحدهما يمثل الطول والآخر يمثل العرض.

نطبق على القواعد السابقة

$16) x^{2} + x - 72 = (x + 9) (x - 8)$

$17) x^{2} - 8 x - 9 = (x + 1) (x - 9)$

$18) x^{2} + 2 x - 48 = (x + 8) (x - 6)$

أحللُ كلًّ ممّا يأتي:

$19) 3 x^{3} y + 18 x^{2} y - 21 x y = 3 x y (x^{2} + 6 x - 7)$

$= 3 x y (x + 7) (x - 1)$

$20) 2 x^{3} - 2 x^{2} - 4 x = 2 x (x^{2} - x - 2)$

$= 2 x (x - 2) (x + 1)$

$21) 2 x^{3} - 4 x^{2} - 6 x = 2 x (x^{2} - 2 x - 3)$

$= 2 x (x - 3) (x + 1)$

$22) 5 x^{3} y - 35 x^{2} y + 50 x y = 5 x y (x^{2} - 7 x + 10)$

$= 5 x y (x - 5) (x - 2)$

$23) 3 x^{3} - 6 x^{2} - 9 x = 3 x (x^{2} - 2 x - 3)$

$= 3 x (x - 3) (x + 1)$

$24) 4 x^{3} - 8 x^{2} - 12 x = 4 x (x^{2} - 2 x - 3)$

$= 4 x (x - 3) (x + 1)$

25 ) صحةٌ : تقومُ مؤسسةُ الحسينِ للسرطانِ بحملةِ توعيةٍ بأهميةِ الفحصِ المبكرِ للسرطانِ، عَنْ طريقِ لوحاتٍ إعلانيةٍ مستطيلةِ الشكلِ على الطّرقاتِ. إذا كانت مساحة إحدى هذهِ اللوحاتِ $x^{2} + 14 + 48$ مترًا مربعًا وعرضُها $x + 6$ مترًا، فأجدُ طولَ اللوحةِ ومحيطَها بدلالةِ $x$

الحل :

أولاً بما أننا نعلم العرض والمساحة ، إذن يمكن أن نجد الطول عن طريق تحليل المساحة كالتالي :

$(x^{2} + 14 x + 48) = (x + 6) (x + 8)$

بما أن العرض يساوي $(x + 6)$ إذاً الطول يساوي $(x + 8)$ .

ثانياً : نجد المحيط حيث

$p = 2 l + 2 w$

$= 2 (x + 8) + 2 (x + 6)$

$= 2 x + 16 + 2 x + 12$

$= 4 x + 28 = 4 (x + 7)$

ورقٌ صحيٌّ: علبةُ ورقٍ صحيٍّ على شكلِ متوازي مستطيلاتٍ، حجمُهُ $x^{3} + 5 x^{2} + 4 x$ سنتيمترًا مكعبًا. أجدُ قياسًا ممكنًا لكلٍّ مِنْ طولِ العلبةِ وعرضِها وارتفاعِها بدلالةِ $x$ .

الحل :

$x^{3} + 5 x^{2} + 4 x = x (x^{2} + 5 x + 4)$

$= x (x + 4) (x + 1)$

حيث يمكن أن يمثل الطول $(x + 4)$ ويمكن أن يمثل العرض $(x + 1)$ والإرتفاع يساوي $x$

تبريرٌ: أجدُ القيمَ الممكنةَ للعددِ الصحيحِ m في كلٍّ ممّا يأتي، بحيثُ يكونُ ثلاثيُّ الحدودِ قابلً للتحليلِ، ثُمَّ أحللُهُ:

$27) x^{2} + m x - 15$

لمعرفة القيم الممكنة ل m يجب أن نعرف أزواج الأعداد الصحيحة التي حاصل ضربها 15 وهي : ${15, 1} {5, 3}$

وبما أن ال 15 سالبة فإن العددين مختلفين في الإشارة .
ومنه فإن القيم الممكنة لـ m هي كالتالي :

$1) x^{2} + m x - 15 = x^{2} + (15 + - 1) x - 15 = x^{2} + 14 x - 15$

$2) x^{2} + m x - 15 = x^{2} + (1 + - 15) x - 15 = x^{2} - 14 x - 15$

$3) x^{2} + m x - 15 = x^{2} + (5 + - 3) x - 15 = x^{2} + 2 x - 15$

$4) x^{2} + m x - 15 = x^{2} + (3 + - 5) x - 15 = x^{2} - 2 x - 15$

$28) x^{2} - 7 x + m$

لمعرفة القيم الممكنة ل m يجب أن نعرف أزواج الأعداد الصحيحة التي حاصل جمعها $- 7$ وهي :

$1) x^{2} - 7 x + m = x^{2} (- 4 - 3) x + (- 4 * - 3)$

$= x^{2} - 7 x - 18$

$2) x^{2} - 7 x + m = x^{2} (- 5 - 2) x + (- 5 * - 2)$

$= x^{2} - 7 x + 10$

$3) x^{2} - 7 x + m = x^{2} (- 1 - 6) x + (- 1 * - 6)$

$= x^{2} - 7 x + 6$

$4) x^{2} - 7 x + m = x^{2} (- 10 + 3) x + (- 10 * 3)$

$= x^{2} - 7 x - 30$

$5) x^{2} - 7 x + m = x^{2} (- 9 + 2) x + (- 9 * 2)$

$= x^{2} - 7 x - 18$

29) تحدٍّ: أحللُ المقدارَ ${(x - 3)}^{2} - 2 (x - 3) - 8$ .

الحل يمكن معاملة $(x - 3)$ كمتغير منفرد ولتسهيل الفكرة نفرض أن

$y = x - 3$

ومنه يصبح المقدار الجبري كالتالي :

$y^{2} - 2 y - 8 = (y - 4) (y + 2)$

الآن نرجع القيم الأصلية بدلاً من y .

$(y - 4) (y + 2) = (x - 3 - 4) (x - 3 + 2)$

$= (x - 7) (x - 1)$

30 ) تحدٍّ: في الشكلِ المجاورِ مستطيلٌ بُعداهُ $x + b, x + a$ ، قُسِّمَ إلى أربعةِ أجزاءٍ مساحةُ اثنَينِ منها $x^{2}$ و 6 وحدات مربعة ، أبيّنُ أنّهُ توجدُ قيمتانِ ممكنتانِ لكلٍّ مِنْ a و b .

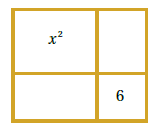
المساحة الأولى هي مربع وتساوي $x^{2}$ حيث يمثل طول ضلع هذا المربع x

المساحة الأولى هي مستطيل وتساوي 6 واحتماليات أبعاده الممكنة هي $L = 3, W = 2$

$L = 6, W = 1$

وعليه فإن الاحتمالات الممكنة لأبعاد المربع هي :

$(x + 6) (x + 1), (x + 3) (x + 2)$

31) أكتشفُ الخطأَ: حللَ كلٌّ مِنْ آدمَ وماريا العبارةَ $y^{2} + 6 y - 16$ مَنْ منهُما إجابتُهُ صحيحةٌ؟ أبرّرُ إجابتي.

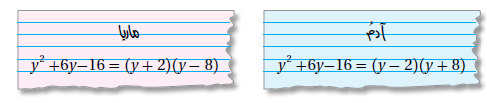
الحل الصحيح هو حل آدم حيث اختار عددان ضربهما 16- ومجموعهما 6+

بينما أخطأت ماريا وذلك لأنها اختارت عددين مجموعهما 6- وليس 6+

أكتب : كيفَ أحددُ قيمةَ كلٍّ مِنْ m و n عند تحليل $y^{2} - 3 y - 4$ على صورةِ $(y + m) (y + n)$ .

- إذا كانت إشارة الحد الأخير موجبة فإن لـ m و n نفس الإشارة (سواء موجبة أو سالبة) ويعتمد تحديد الإشارة على إشارة الحد الأوسط .

- إذا كانت إشارة الحد الأخير سالبة فإن لـ m و n إشارتين مختلفتين ويعتمد تحديد الإشارة على إشارة الحد الأوسط ،

أسئلة كتاب التمارين

أحللُ كلًّ ممّا يأتي:

تذكر : إذا كانت المعادلة على صورة $x^{2} + b x + c$ ، فإننا نبحث عن عددين حاصل ضربهما c

ومجموعهما b

$1) x^{2} + 2 x + 1 = (x + 1) (x + 1)$

$2) x^{2} + 9 x + 20 = (x + 5) (x + 4)$

$3) x^{2} + 8 x + 7 = (x + 7) (x + 1)$

$4) x^{2} - 7 x + 10 = (x - 5) (x - 2)$

$5) x^{2} - 5 x - 6 = (x - 2) (x - 3)$

$6) x^{2} + 3 x - 40 = (x + 8) (x - 5)$

$7) x^{2} + 16 x - 17 = (x + 17) (x - 1)$

$8) 100 + x^{2} - 29 x = x^{2} - 29 x + 100$

$= (x - 25) (x - 4)$

$9) x^{2} + 99 x - 100 = (x + 100) (x - 1)$

أجدُ جميعَ القيمِ الممكنةِ للعددِ الصحيحِ m بحيثُ يكونُ المقدارُ الجبريُّ قابلً للتحليلِ:

$10) x^{2} + m x + 6$

لمعرفة القيم الممكنة ل m يجب أن نعرف أزواج الأعداد الصحيحة التي حاصل ضربها 6 وهي :

${2, 3}$

${6, 1}$

وبما أن ال 6 موجبة فإن العددين متشابهين في الإشارة . ومنه فإن الاحتمالات الممكنة هي :

$1) x^{2} + m x + 6 = x^{2} + (2 + 3) x + 6 = x^{2} + 5 x + 6$

$2) x^{2} + m x + 6 = x^{2} + (6 + 1) x + 6 = x^{2} + 7 x + 6$

$11) x^{2} + m x - 10$

لمعرفة القيم الممكنة ل m يجب أن نعرف أزواج الأعداد الصحيحة التي حاصل ضربها 10 وهي :

${1, 10}$

${2, 5}$

وبما أن ال 10- سالبة فإن العددين مختلفين في الإشارة . ومنه فإن الاحتمالات الممكنة هي :

$1) x^{2} + m x - 10 = x^{2} + (1 + - 10) x - 15 = x^{2} - 9 x - 10$

$2) x^{2} + m x - 10 = x^{2} + (10 + - 1) x - 15 = x^{2} + 9 x - 10$

$3) x^{2} + m x - 10 = x^{2} + (5 + - 2) x - 15 = x^{2} + 3 x - 10$

$4) x^{2} + m x - 10 = x^{2} + (2 + - 5) x - 15 = x^{2} - 3 x - 10$

$12) x^{2} - 7 x + m, m > 0$

لمعرفة القيم الممكنة ل m يجب أن نعرف أزواج الأعداد الصحيحة التي حاصل جمعها 7-

$1) x^{2} - 7 x + m = x^{2} (- 4 - 3) x + (- 4 * - 3)$

$= x^{2} - 7 x + 12$

$2) x^{2} - 7 x + m = x^{2} (- 5 - 2) x + (- 5 * - 2)$

$= x^{2} - 7 x + 10$

$3) x^{2} - 7 x + m = x^{2} (- 1 - 6) x + (- 1 * - 6)$

$= x^{2} - 7 x + 6$

13) ماءٌ: خزانُ ماءٍ على شكلِ متوازي مستطيلاتٍ حجمُهُ $2 x^{3} + 4 x^{2} - 30 x$ مترًا مكعبًا. إذا كانَ ارتفاعُ الخزّانِ $2 x$ مترًا، فأجدُ بُعدَينِ ممكنَينِ لقاعدتِهِ بدلالةِ $x$ .

الحل :

لإيجاد بعدين لقاعدته نحلل المقدار المعبر عن حجمه كالتالي :

$2 x^{3} + 4 x^{2} - 30 x = 2 x (x^{2} + 2 x - 15)$

$= 2 x (x + 5) (x - 3)$

حيث $2 x$ يعبر عن الارتفاع ، و $(x + 5)$ يعبر عن عن الطول و $(x - 3)$ يعبر عن العرض.

14) أجدُ مقدارًا جبريًّا يمكنُ أَنْ يمثلَ محيطَ مستطيلٍ مساحتُهُ $x^{2} + 14 x + 24$ وحدةً مربعةً.

الحل : لنجد المحيط يجب أن نجد الطول والعرض عن طريق التحليل ، ثم نطبق على قانون محيط المستطيل كالتالي .

$x^{2} + 14 x + 24 = (x + 12) (x + 2)$

$P = 2 L + 2 w$

$= 2 (x + 12) + 2 (x + 2)$

$= 2 x + 24 + 2 x + 4$

$= 4 x + 28 = 4 (x + 7)$

15) تبريرٌ: إذا كانَتْ مساحةُ غرفةٍ $(x^{2} + 22 x + 121)$ مترًا مربعًا، فَهَلْ يمكنُ أَنْ تكونَ الغرفةُ مربعةَ الشكلِ؟ أبرّرُ إجابتي.

الحل :

باختصار نحلل المقدار ، فإذا حصلنا على بعدين متساويين فإنه يمثل مربع .

$x^{2} + 22 x + 121 = (x + 11) (x + 11)$

وعليه فإن المقدار يمثل مربع .

حواسيبُ: يظهرُ على شاشةِ الحاسوبِ المجاورةِ نافذةُ برنامجٍ مصغَّرةٌ مساحتُها $x^{2} - 8 x + 15$ سنتيمترًا مربعًا:

16) أجدُ ارتفاعَ نافذةِ البرنامجِ بدلالةِ x

أولاً نجد عرض النافذة عن طريق تحليل مقدار المساحة الخاص بها :

$x^{2} - 8 x + 15 = (x - 5) (x - 3)$

وعليه فإن عرض النافذة يساوي عرض الشاشة ويساوي $x - 3$ ومنه فإن النافذة غير مرتفعة حيث ارتفاعها يساوي صفر

17) إذا كانَتْ مساحةُ نافذةِ البرنامجِ تساوي $\frac{1}{4}$ مساحةِ الشاشةِ، فأجدُ طولَ الشاشةِ.

$x^{2} - 8 x + 15 = \frac{(x - 3) * L}{4}$

$\frac{(x - 3) (x - 5)}{(x - 3)} = \frac{(x - 3) * L}{4 (x - 3)}$

$x - 5 = \frac{L}{4}$

$L = 4 (x - 5)$

رياضيات فصل أول

الثامن

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS