حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 77
أصنف كل من المثلثات الآتية حسب قياسات زواياها ، وأبرر إجابتي :

الحل :
| مثلث حاد الزوايا ؛ لأن زواياه الثلاث حادة. | 1) |
| مثلث قائم الزاوية ؛ لأن إحدى زواياه قائمة . | 2) |
| مثلث منفرج الزاوية ؛ لأن إحدى زواياه منفرجة . | 3) |
أتحقق من فهمي صفحة 78
أصنف كل من المثلثات الآتية حسب قياسات زواياها ، وأبرر إجابتي :

الحل :
|
إيجاد قياس الزاوية الثالثة ، بفرض الزاوية المجهولة |
1) |
| مجموع زوايا المثلث = | |
| بجمع الزوايا المعلومة . | |
| باستخدام العلاقة بين الجمع والطرح . | |
| بالتبسيط . |
بما أنّ المثلث يحوي زاوية قائمة ، إذن المثلث قائم الزاوية .
| إيجاد قياس الزاوية الثالثة ، بفرض الزاوية المجهولة | 2) |
| مجموع زوايا المثلث = | |
| بجمع الزوايا المعلومة . | |
| باستخدام العلاقة بين الجمع والطرح . | |
| بالتبسيط . |
بما أنّ المثلث يحوي زاوية قياسها وهي زاوية منفرجة ، إذن المثلث منفرج الزاوية .
|
إيجاد الزاوية المجاورة للزاوية وهما على مستقيم ، ومجموع الزوايا التي على مستقيم ولها الرأس نفسه =
|
3) 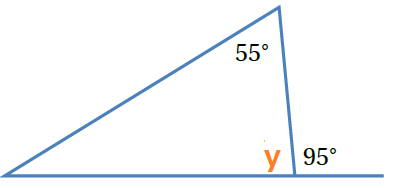 |
| نفرض الزاوية y ، مجموع الزوايا التي على مستقيم = | |
| باستخدام العلاقة بين الجمع والطرح . | |
| بالتبسيط . |
•• والآن نجد الزاوية المجهولة في المثلث :
| إيجاد قياس الزاوية الثالثة ، بفرض الزاوية المجهولة | 3) |
| مجموع زوايا المثلث = | |
| بجمع الزوايا المعلومة . | |
| باستخدام العلاقة بين الجمع والطرح . | |
| بالتبسيط . |
بما أن زوايا المثلث جميعها حادة ، إذن المثلث حاد الزوايا .
أسئلة أتدرب وأحل المسائل
أصنف كل من المثلثات الآتية حسب قياسات زواياها ، وأبرر إجابتي :
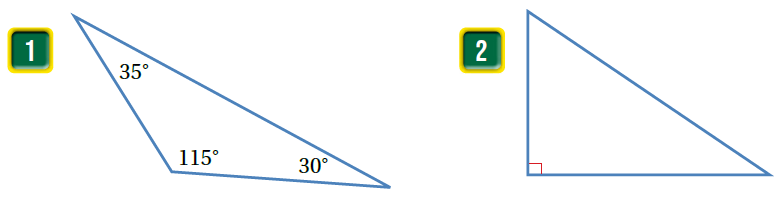 |
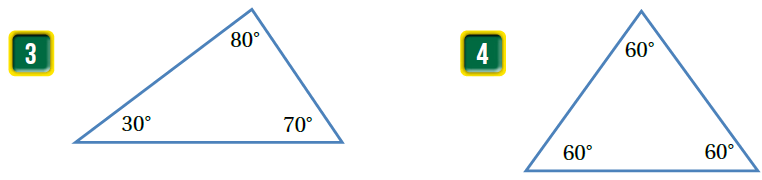 |
 |
الحل :
| مثلث منفرج الزاوية لوجود زاوية قياسها | 1) |
| مثلث قائم الزاوية لوجود زاوية | 2) |
| مثلث حاد الزوايا لان زواياه الثلاث حادة | 3) |
| مثلث حاد الزوايا لان زواياه الثلاث حادة | 4) |
| مثلث حاد الزوايا لان زواياه الثلاث حادة | 5) |
| مثلث منفرج الزاوية لوجود زاوية قياسها | 6) |
أصنف كل من المثلثات الآتية حسب قياسات زواياها ، وأبرر إجابتي :
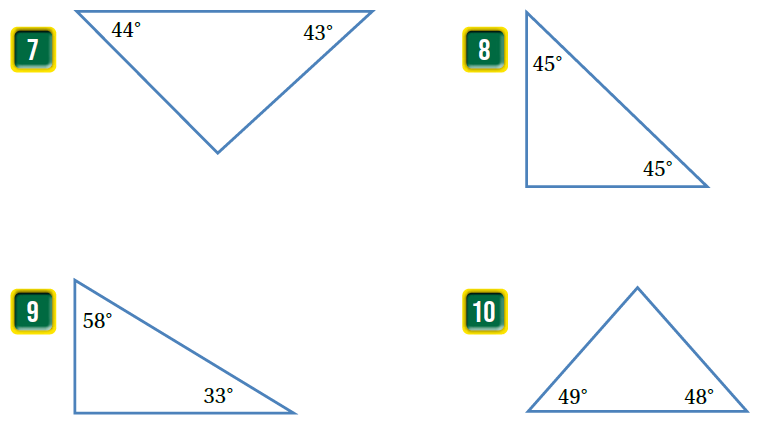
الحل :
|
الخطوة الاولى ايجاد الزاوية المجهولة ، ثم تصنيف المثلث التصنيف : مثلث منفرج الزاوية لوجود زاوية قياسها وهي زاوية منفرجة . |
|
7) |
|
الخطوة الاولى ايجاد الزاوية المجهولة ، ثم تصنيف المثلث التصنيف : مثلث قائم الزاوية لوجود زاوية قياسها |
|
8) |
|
الخطوة الاولى ايجاد الزاوية المجهولة ، ثم تصنيف المثلث التصنيف : مثلث حاد الزوايا ؛ لأن زواياه الثلاث حادة |
|
9) |
|
الخطوة الاولى ايجاد الزاوية المجهولة ، ثم تصنيف المثلث التصنيف : مثلث حاد الزوايا ؛ لأن زواياه الثلاث حادة |
|
10) |
أصنف كل من المثلثات المعطاة قياساتها حسب أطوال أضلاعها وقياسات زواياها ، وأبرر إجابتي :
11) الأضلاع : الزوايا :
الحل :
التصنيف حسب أطوال الأضلاع : مثلث متطابق الضلعين؛ لوجود ضلعين لهما الطول نفسه .
التصنيف حسب قياس الزوايا : مثلث منفرج الزاوية لوجود الزاوية المنفرجة .
12) الأضلاع : الزوايا :
الحل :
التصنيف حسب أطوال الأضلاع : مثلث مختلف الأضلاع ؛ لأنه لا يوجد ضلعين في المثلث لهما الطول نفسه.
التصنيف حسب قياس الزوايا : مثلث منفرج الزاوية لوجود الزاوية المنفرجة
13) مثلث قائم الزاوية فيه زاوية قياسها . ما قياس الزاوية الأخرى ؟
الحل :
بما أن المثلث قائم الزاوية إذن يوجد فيه زاوية قياسها ، باستخدام حقيقة أن مجموع قياس زوايا المثلث = نجد قياس الزاوية الثالثة :
إذن قياس الزاوية الثالثة = 60
|
14) ألعاب: تُنظم كرات البلياردو في بداية اللعبة على صورة مثلث. بينما كان ينظم أحمد الكرات رسم مثلثًا حولها، فوجد أن زواياه جميعها متطابقة ، فما قياس كل زاوية ؟ وما نوع المثلث؟ |
 |
الحل :
بما أن مجموع قياس زوايا المثلث = ، وزواياه الثلاث متساوية في القياس ، إذن نقسم 180 على 3 لنجد قياس كل منها :
إذن قياس كل زاوية في المثلث = ، وهي زاوية حادة ، إذن المثلث حاد الزوايا ، لأن قياسات زواياه الثلاث حادة .
15) مسألة مفتوحة : أرسم مثلثًا قائم الزاوية ومتطابق الضلعين على الشبكة أدناه.

الحل :

16) اكتشف الخطأ : تقول مرح إن المثلث المنفرج الزاوية يمكن أن يكون قائم الزاوية أيضًا. هل هي على صواب؟ أبرر إجابتي.
الجواب : مقولة مرح غير صحيحة ؛ لأن مجموع زوايا المثلث = ، وإذا كان المثلث منفرج الزاوية فهذا يعني وجود زاوية قياسها أكبر من ، وعليه : فيجب أن يكون مجموع الزاويتين الآخريين أقل من
17) تبرير : مثلث قياسا زاويتين من زواياه الثلاث ° 23 و° 67 ؛ هل هذا المثلث حاد الزوايا أم قائم الزاوية أم منفرج الزاوية؟ أبرر إجابتي.
الحل :
|
مجموع زوايا المثلث = قياس الزاوية الثالثة = إّذن المثلث قائم الزاوية لوجود زاوية قياسها |
أسئلة كتاب التمارين
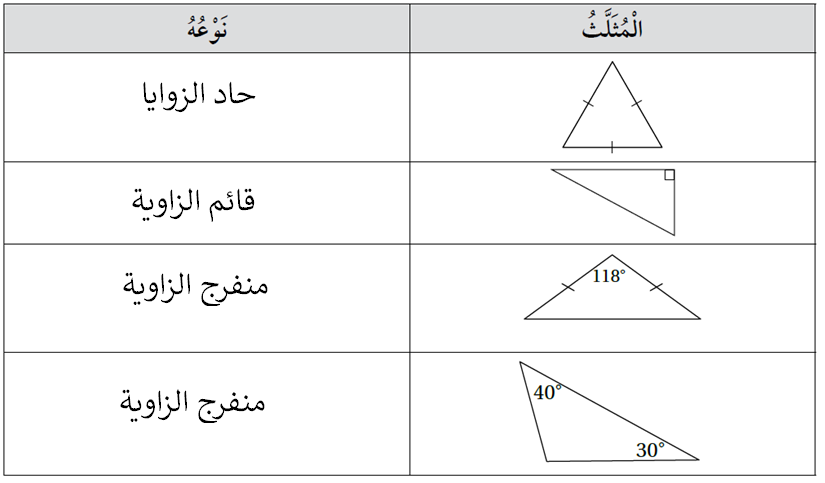
أصنف كل مثلث في الجدول الآتي إلى حاد الزوايا ، أو منفرج الزاوية ، أو قائم الزاوية :
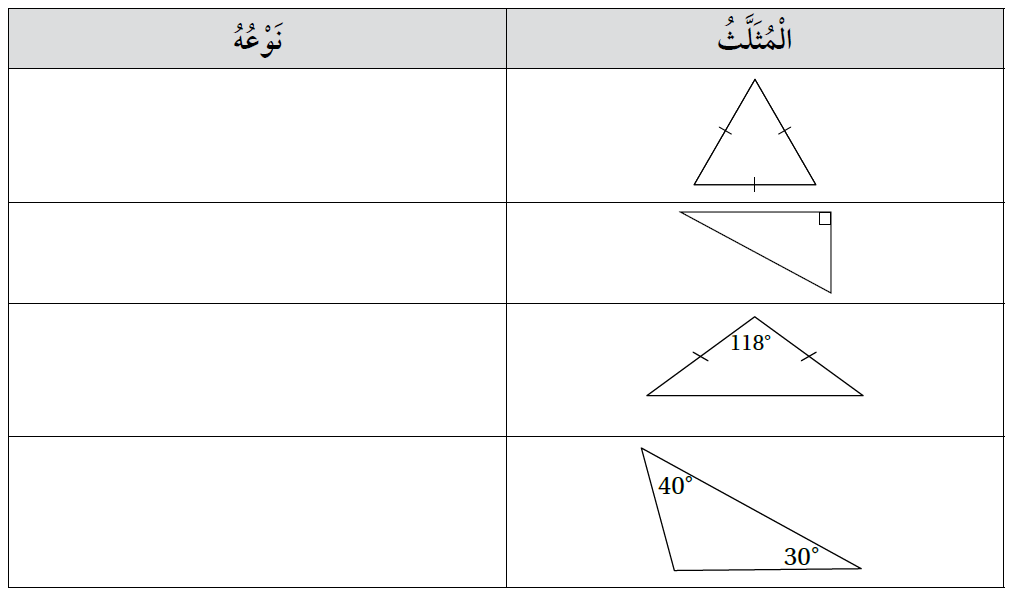
الحل :
أصنف المثلثات الآتية حسب قياسات زواياها ، واذكر السبب .
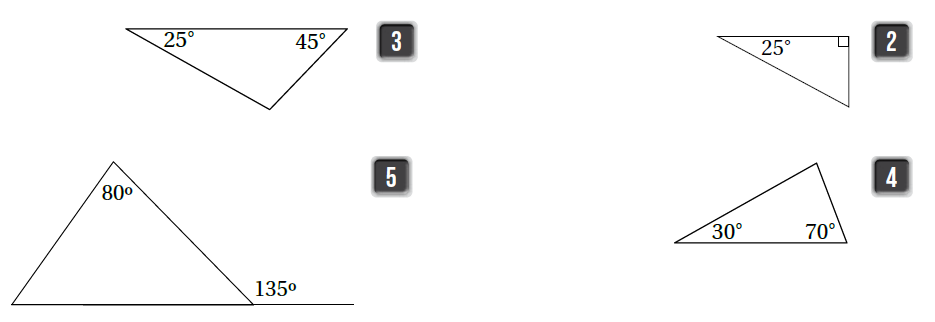
الحل :
| قائم الزاوية لوجود زاوية قياسها 90 درجة. | 2) | |
| منفرج الزاوية لأن إحد زواياه زاوية منفرجة. | 3) | |
| حاد الزوايا لأن قياس زواياه الثلاث حادة . | 4) | |
|
ايجاد الزاوية المجاورة للزاوية 135 ، وهي زوايا على مستقيم مشتركة في رأس واحد ، مجموعها = 180 ، فينتج قياس الزاوية = 45 تصنيف المثلث : حاد الزوايا لأن قياس زواياه الثلاث حادة . |
5) |
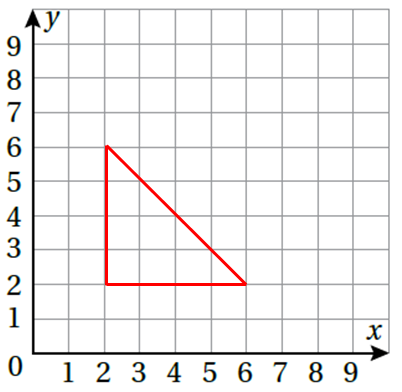
6) أرسم مُثلثا رؤسه ( 2 , A(2, 2) , B(2, 6) , C(6 ، ثُمّ أصنّفه حسب أطوال أضلاعه وقياسات زواياه. أبرر إجابتي.
الحل :
|
التصنيف حسب أطوال الأضلاع : متطابق الضلعين ؛ لأن فيه ضلعان لهما الطول نفسه . التصنيف حسب قياسات الزوايا : مثلث قائم الزاوية ؛ لأن فيه زاوية قائمة.
|
 |