تطبيقات القيم القصوى - الشرح - الصف التوجيهي علمي - رياضيات فصل أول - مدرسة جواكاديمي

تعلمت سابقاً إيجاد القيم القصوى المطلقة لاقتران محدد باستخدام التفاضل،

و تٌعدّ تطبيقات هذا الموضوع من أهم موضوعات التفاضل في الحياة العملية.
و يمكنك اتباع الاستراتيجية الآتية في حل مسائل القيم القصوى:

1. أفهم المسألة: عن طريق قراءتها جيداً و تحديد المعطيات و المطلوب

2. أرسم مخططاً: أرسم مخططاً يمثّل المسألة، موضحاً عليه معلومات المسألة،

و مستخدماً رموزاً مناسبة للكمية المراد إيجاد قيمتها القصوى، و للكميات الأخرى،

و كتابة الاقتران الذي يمثل الكمية المراد ايجاد قيمتها القصوى، و بدلالة متغير واحد.

3. أحدد مجال الاقتران: أحدد مجال الاقتران (إن أمكن) لمعرفة منطقية و صحة الحل.

4. أجد قيم الاقتران الحرجة و قيمتيه عند طرفي الفترة.

5. أجد القيمة القصوى المطلوبة باستخدام اختبار المشتقة الأولى او اختبار المشتقة الثانية.

و من المهم في مسائل القيم القصوى، تحديد الاقتران المراد ايجاد قيمته العظمى او الصغرى

بدلالة متغير واحد فقط، و ذلك باستخدام معلومات المسألة، و كذلك تحديد مجاله ( إن أمكن).

* فإذا كان المطلوب إيجاد أكبر حجم ممكن،

يكون الاقتران الذي يمثل الحجم (V) . هو الاقتران المطلوب قيمته العظمى المطلقة.

* وإذا كان المطلوب أقل بعد ممكن بين شخصين،

فيكون الاقتران يمثل المسافة (d) هو الاقتران المطلوب إيجاد قيمته الصغرى المطلقة، و هكذا.

ولتوضيح خطوات الحل، دعنا ندرس هذه الأمثلة:

مثال 1:

صندوق على شكل متوازي مستطيلات قاعدته مربعة الشكل،

ومجموع ابعاده 30cm، أجد أبعاد الصندوق ليكون حجمه اكبر ما يمكن

الخطوة 1: أرسم مخططاً

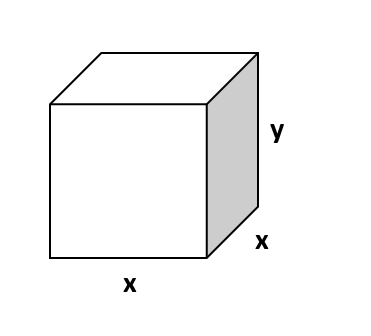افرض أن طول ضلع القاعدة المربعة x، و ارتفاع الصندوق y،

ويكون مجموع أبعاد الصندوق 30cm.

x + x + y = 30

y = 30 - 2x

الخطوة 2: المطلوب:ايجاد ابعاد الصندوق ليكون حجمه اكبر ما يمكن

( أي: القيمة العظمى المطلقة لحجم الصندوق)

نكتب الاقتران الذي يمثل حجم الصندوق بدلالة متغير واحد.

$v = L . w . h L = w = x h = y v = x^{2} y v = x^{2} . (30 - 2 x) b u t y = 30 - 2 x v (x) = 30 x^{2} - 2 x^{3} R a n g e : 0 \leq x \leq 15 a n d y \geq 0 30 - 2 x \geq 0 x \geq 15$

الخطوة 3: إيجاد القيم الحرجة للاقتران، ثم تحديد القيمة العظمى المطلقة

$v^{'} (x) = 60 x - 6 x^{2} 0 = 6 x (10 - x) x = 0, x = 10$

قيم x الحرجة في الفترة(0,15) هي x = 10

v(0) = 0 , x=0

v(15) = 0 , x=15

القيمة العظمى المطلقة v(10) = 1000 , x=10

إذن: أبعاد الصندوق ذي أكبر حجم $1000 c m^{3}$ هي:

x = 10cm , y = 10cm

مثال2: انطلق القارب A من النقطة Q في البحر غرباً نحو النقطة P .والتي تبعد 20km عن Q

وسرعة 2km/min، وفي اللحظة نفسها انطلق القارب B من النقطةP في مسار مستقيم

بزاوية $60^{\circ}$ شمال الشرق بسرعة 3km/min. بعد كم دقيقة من انطلاق القاربين

تكون المسافة بينهما أقل ما يمكن، علماً بأن القاربين سارا مدة 10min.

الخطوة 1: أرسم مخططاً

يمكن رسم المخطط المجاور الذي يمثل المسألة بعد مرور t من الدقائق، بعد الانطلاق يكون:

QA = 2t km

PB = 3t km

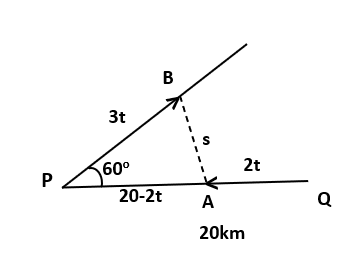
المطلوب: القيمة الصغرى المطلقة للمسافة s بين القاربين A و B

الخطوة 2: الاقتران الذي يمثل المسافة s هو:

$s = \sqrt{P A^{2} + P B^{2} - 2 (P A) (P B) c o s (60^{\circ})} s (t) = \sqrt{{(20 - 2 t)}^{2} + {(3 t)}^{2} - 2 (20 - 2 t) (3 t) (\frac{1}{2})} s (t) = \sqrt{400 - 80 t + 4 t^{2} + 9 t^{2} - 60 t + 6 t^{2}} s (t) = \sqrt{19 t^{2} - 140 t + 400}$

المجال: $0 \leq t \leq 10$

الخطوة 3:

$s^{'} (t) = \frac{38 t - 140}{2 \sqrt{19 t^{2} - 140 t + 400}} 0 = 38 t - 140 t = \frac{140}{38} = \frac{70}{19} = 3.7 m i n$

نقارن:

s(0) = 20km , t=0min

s(10) = 30km, t=10min

s( $\frac{70}{19}$ ) = 11.9 km

فتكون القيمة الصغرى المطلقة للمسافة هي 11.9km تقريباً بعد مرور min $\frac{70}{19}$ من الانطلاق.

و يمكن استخدام تطبيقات القيم القصوى في ايجاد اكبر ربح ممكن

او اكبر ايراد ممكن او اقل تكلفة ممكنة في المسائل الاقتصادية حيث أن:

p(x) = R(x) - C(x)

حيث:

P(x): هو اقتران الربح عند بيع x من القطع.

R(x): هو اقتران الايراد عند بيع x من القطع.

C(x): هو اقتران التكلفة عند انتاج x من القطع.

مثال 3:

يمثل الاقتران $z = 300 - 0.4 x$ سعر الشاشة بالدينار الذي حددته الشركة عند بيع x من الشاشات،

ويمثل الاقتران $C (x) = 6000 + 0.2 x^{2}$ تكلفة انتاج x شاشة.

ما عدد الشاشات اللازم بيعها لتحقيق اكبر ربح؟

الخطوة 1: نجد اقتران الربح و الذي نريده أن يكون قيمة عظمى مطلقة،

نفرض أن x يمثل عدد الشاشات المبيعة.

اقتران الايراد هو: سعر الشاشة x عددها:

$R (x) = z . x R (x) = (300 - 0.4 x) x R (x) = 300 x - 0.4 x^{2} C (x) = 6000 + 0.2 x^{2} P (x) = R (x) - C (x) P (x) = (300 x - 0.4 x^{2}) - (6000 + 0.2 x^{2}) P (x) = - 0.6 x^{2} + 300 x - 6000, x \geq 0$

الخطوة 2:

$P^{'} (x) = - 1.2 x + 300 0 = - 1.2 x + 300 x = \frac{300}{1.2} \Rightarrow x = 250$

نستخدم اختبار المشتقة الثانية لتحديد نوع القيمة القصوى عند x = 250

$P^{''} (x) = - 1.2 < 0$

إذن عند x = 750، اقتران الربح يكون له قيمة عظمى مطلقة،

إذن تحقق الشركة اكبر ربح ممكن عند بيع 250 شاشة

رياضيات فصل أول

التوجيهي علمي

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS