تطبيقات القيم القصوى - حل اسئلة الدرس - الصف التوجيهي علمي - رياضيات فصل أول - مدرسة جواكاديمي

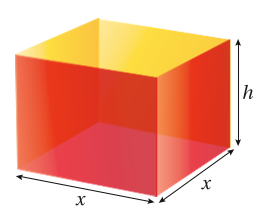
ترغب شركة في تصميم صندوق مفتوح من الأعلى ، وقاعدته مربعة

الشكل ، ومساحة سطحه الكلية $1080 c m^{2}$ كما في الشكل المجاور.

أجد أبعاد الصندوق ليكون حجمه أكبر ما يُمكن.

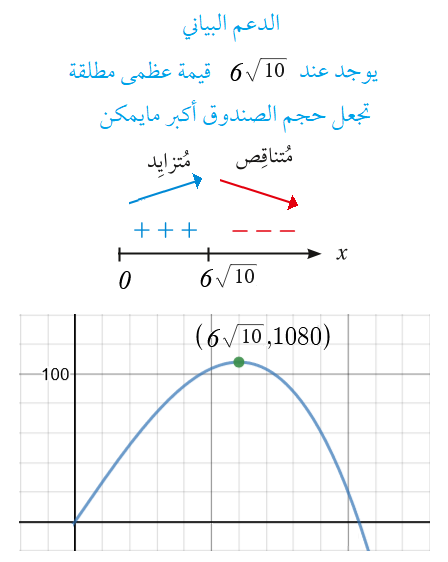
الاقتران الهدف هو الحجم $V = x^{2} h$

$S o l u t i o n : V = x^{2} h B u t A = x^{2} + 4 x h 1080 = x^{2} + 4 x h \Rightarrow h = \frac{1080 - x^{2}}{4 x} V = x^{2} (\frac{1080 - x^{2}}{4 x}) = \frac{1}{4} (1080 x - x^{3}) V (x) = \frac{1}{4} (1080 x - x^{3}) V^{'} (x) = \frac{1}{4} (1080 - 3 x^{2}) = 0 \Rightarrow 1080 - 3 x^{2} = 0 \Rightarrow x^{2} = 360 \Rightarrow x = 6 \sqrt{10} V^{"} (x) = \frac{1}{4} (- 6 x) \Rightarrow V " (6 \sqrt{10}) = \frac{1}{4} (- 6 (6 \sqrt{10})) < 0 w h e n x = 6 \sqrt{10} c m t h e n h = \frac{1080 - {(6 \sqrt{10}))}^{2}}{4 (6 \sqrt{10}))} = \frac{30}{\sqrt{10}} c m$

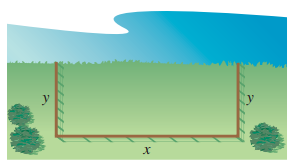خطّط مُزارع لتسييج حظيرة مستطيلة الشكل قرب نهر كما فى الشكل المجاور

وحدِّد مساحة الحظيرة بـ $245000 {cm}^{2}$ لتوفير كمية عشب كافية لأغنامه.

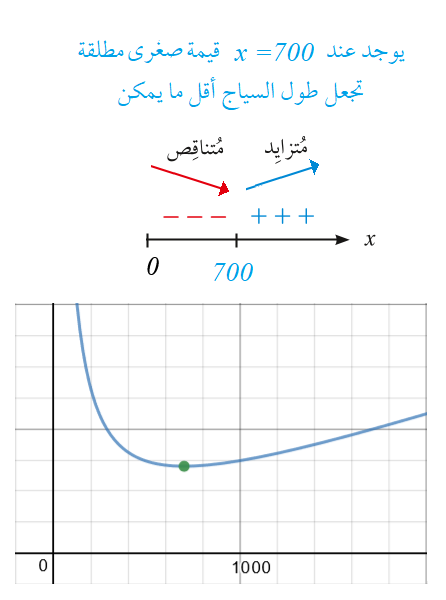
أجد أبعاد الحظيرة التي تجعل طول السياج أقل ما يمكن.

علمًا بأنَّ الجزء المُقابِل للنهر لا يحتاج إلى تسييج.

الاقتران الهدف هو طول السياج $L = x + 2 y$

$S o l u t i o n : L = x + 2 y b u t A = x y 245000 = x y \Rightarrow y = \frac{245000}{x} L = x + 2 y = x + 2 (\frac{245000}{x}) L (x) = x + \frac{490000}{x} L' (x) = 1 - \frac{490000}{x^{2}} = 0 \Rightarrow x^{2} = 490000 \Rightarrow x = 700 c m L'' (x) = \frac{980000}{x^{3}} \Rightarrow L'' (700) = \frac{980000}{{(700)}^{3}} > 0$

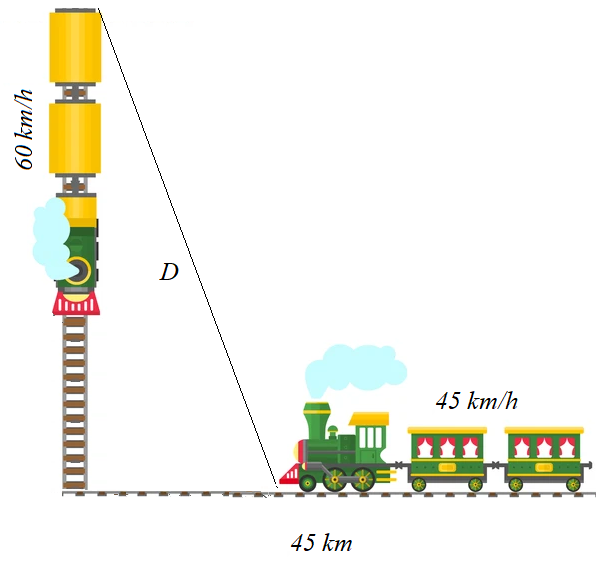انطلق قطار من إحدى المحطّات الساعة $10 : a m$ وتحرّك في اتجاه الجنوب بسرعة $60 km / h$

حيث المحطّة التالية. وفي الوقت نفسه ، انطلق قطار آخر نحو الغرب بسرعة $45 k m / h$ .

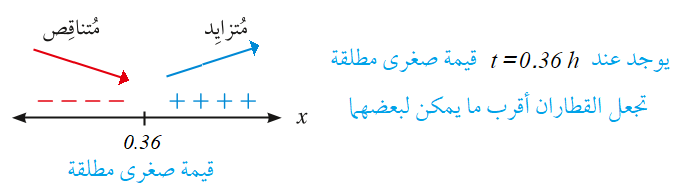
ثم وصل إلى المحطة نفسها الساعة $11 : a m$ . في أيٍّ ساعة يكون القطاران أقرب ما يُمكِن إلى بعضهما؟

الاقتران الهدف هو البعد بين القطارين $D = \sqrt{{(45 - x)}^{2} + y^{2}}$

$S o l u t i o n : D = \sqrt{{(45 - x)}^{2} + y^{2}} b u t x = 45 t, y = 60 t \Rightarrow D (t) = \sqrt{{(45 - 45 t)}^{2} + {(60 t)}^{2}} \Rightarrow D' (t) = \frac{2 (45 - 45 t) (- 45) + 7200 t}{2 \sqrt{{(45 - 45 t)}^{2} + {(60 t)}^{2}}} = 0 t h e n 2 (45 - 45 t) (- 45) + 7200 t = 0 45 t - 45 + 80 t = 0 \Rightarrow 125 t = 45 \Rightarrow t = 0.36 h$

حل التحقق من الفهم الوارد صفحة 128

يبيع متجر $200$ شاشة تلفاز شهربًا بسعر $350 J D$ للشاشة الواحدة.

وقد أشار مسح للسوق أَعَدَّهُ خبير التسويق في المتجر إلى

أنَّ عدد الشاشات المَبيعة شهريًا يزيد بمقدار شاشة عند كل

خصم مقداره ، من سعر الشاشة الواحدة.

أجد سعر بيع الشاشة الواحدة الذي يُحقّق للمتجر أعلى إيراد مُمكن.

الحل:

بفرض أن مبلغ الخصم على الشاشة الواحدة هو x دينار .

وبما أن عدد الشاشات المبيعة شهرياً يزيد بمقدار 20 شاشة لكل 10JD خصم .

لذلك فإن عدد الشاشات المبيعة شهرياً يزيد بمقدار لكل x دينار خصم .

بالتالي فإن سعر الشاشة = 350 - x

عدد الشاشات المبيعة شهرياً = 200 + 2x

اقتران الايراد الشهري = عدد الشاشات × ثمن الشاشة الواحدة

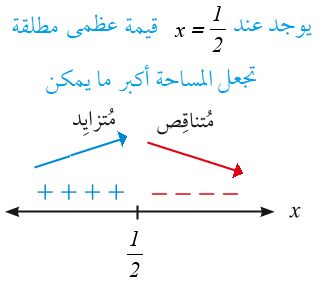
$R (x) = (200 + 20 x) (350 - 10 x) R (x) = - 200 x^{2} + 5000 x + 70000 R^{'} (x) = - 400 x + 500 = 0 \Rightarrow x = 12.5 J D R^{"} (x) = - 4 R^{"} (125) = - 4 < 0$

لذلك فإنه يوجد عند $x = 12.5 J D$ قيمة عظمى مطلقة تجعل الايراد أكبر مل يمكن .

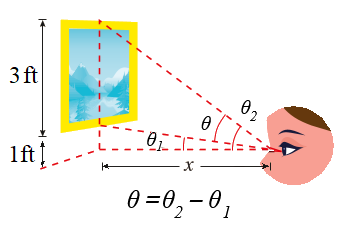نظرت سارة إلى لوحة مُعلّقة على حائط في منزلهاء ارتفاعها $3 ft$ ،

وارتفاع حافتها السفلية $1 ft$ فوق عينها كما في الشكل المجاور.

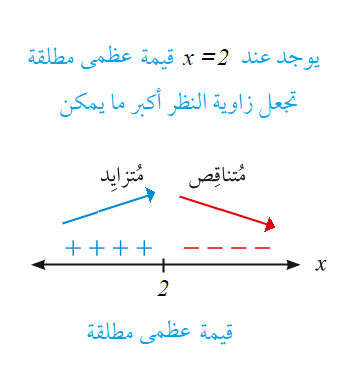
كم مترًا يجب أَنْ تبتعد سارة عن الجدار لتكون زاوية نظرها $θ$ أكبر ما يُمكن؟

الاقتران الهدف هو ظل الزاوية : $t a n θ = t a n (θ_{2} - θ_{1})$

$S o l u t i o n : θ = θ_{2} - θ_{1} t a n θ = t a n (θ_{2} - θ_{1}) = \frac{t a n θ_{2} - t a n θ_{1}}{1 + t a n θ_{2} \times t a n θ_{1}} b u t t a n θ_{2} = \frac{4}{x}, t a n θ_{1} = \frac{1}{x} \Rightarrow t a n θ = \frac{\frac{4}{x} - \frac{1}{x}}{1 + (\frac{4}{x} \times \frac{1}{x})} = \frac{\frac{3}{x}}{1 + \frac{4}{x^{2}}} n o w l e t t a n θ = f (x) f (x) = \frac{3 x}{x^{2} + 4} f^{^{'}} (x) = \frac{3 (x^{2} + 4) - 3 x (2 x)}{(x^{2} + {4)}^{2}} = 0 4 - x^{2} = 0 \Rightarrow x = 2$

أجد النقطة (النقاط) الواقعة على منحنى الاقتران $f (x) = \sqrt{8 x}$ ،

التي هي أقرب ما يُمكِن إلى النقطة $(4, 2)$ .

الحل:

الاقتران الهدف هو البعد بين نقطتين: $D (x) = \sqrt{{(x - 4)}^{2} + {(\sqrt{8 x} - 2)}^{2}}$

$S o l u t i o n : D (x) = \sqrt{{(x - 4)}^{2} + {(\sqrt{8 x} - 2)}^{2}} D^{'} (x) = \frac{2 (x - 4) + 2 (\sqrt{8 x} - 2) \frac{8}{2 \sqrt{8 x}}}{2 \sqrt{{(x - 4)}^{2} + {(\sqrt{8 x} - 2)}^{2}}} = 0 2 (x - 4) + 2 (\sqrt{8 x} - 2) \frac{8}{2 \sqrt{8 x}} = 0 x - 4 + (\sqrt{8 x} - 2) \frac{4}{\sqrt{8 x}} = 0 x - 4 + \frac{4 \sqrt{8 x}}{\sqrt{8 x}} - \frac{8}{\sqrt{8 x}} = 0 x - 4 + 4 - \frac{8}{\sqrt{8 x}} = 0 \Rightarrow x = \frac{8}{\sqrt{8 x}} x^{2} (8 x) = 64 \Rightarrow x^{3} = 8 \Rightarrow x = 2 \Rightarrow y = 4 (2, 4)$

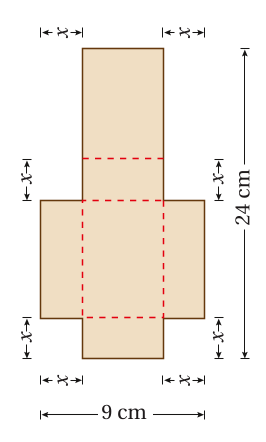قطعة كرتون طولها $24 c m$ وعرضها $9 c m$ أزيل منها مربعان متطابقان

ومستطيلان متطابقان كما فى الشكل المجاور ، بحيث ‏ أمكن طيّها ، وتكوين

صندوق له غطاء منها:

1) أكتب الاقتران $V (x)$ الذى يمثل حجم الصندوق.

$S o l u t i o n : 2 x + 2 y = 24 \Rightarrow y = 12 - x V (x) = x (9 - 2 x) (12 - x) V (x) = 2 x^{3} - 33 x^{2} + 108 x$

2) أحدّد مجال $V (x)$ الاقتران.

$S o l u t i o n : V (x) = x (9 - 2 x) (12 - x) x \geq 0 9 - 2 x \geq 0 \Rightarrow x \leq \frac{9}{2} 12 - x \geq 0 \Rightarrow x \leq 12 x \in (0, \frac{9}{2})$

3) أجد أبعاد الصندوق بحيث يكون حجمه أكبر ما يُمكن.

$S o l u t i o n : V (x) = 2 x^{3} - 33 x^{2} + 108 x V^{'} (x) = 6 x^{2} - 66 x + 108 = 0 x^{2} - 11 x + 18 = 0 (x - 9) (x - 2) = 0 \Rightarrow x = 2$

بتطبيق اختبار المشتقة الثانية نجد انَّ:

$V (x) = 2 x^{3} - 33 x^{2} + 108 x V^{'} (x) = 6 x^{2} - 66 x + 108 V^{''} (x) = 12 x - 66 V^{''} (2) = 12 (2) - 66 = - 42 < 0$

المشتقةيوجد عند $x = 2$ قيمة عظمى مطلقة تجعل حجم الصندوق أكبر ما يمكن

أبعاد القاعدة : {10 ، 5} ، الارتفاع = 2 .

4) أجد النقطة الواقعة على منحنى العلاقة: $4 x^{2} + y^{2} = 4$ ، التي هي أقرب ما يُمكِن إلى النقطة $(0, 1)$ .

الاقتران الهدف هو البعد بين نقطتين: $D (x) = \sqrt{x^{2} + {(\sqrt{4 - 4 x^{2}} - 1)}^{2}}$

$S o l u t i o n : D (x) = \sqrt{x^{2} + {(\sqrt{4 - 4 x^{2}} - 1)}^{2}} D' (x) = \frac{2 x + 2 (\sqrt{4 - 4 x^{2}} - 1) \frac{- 8 x}{2 \sqrt{4 - 4 x^{2}}}}{2 \sqrt{x^{2} + {(\sqrt{4 - 4 x^{2}} - 1)}^{2}}} = 0 x + (\sqrt{4 - 4 x^{2}} - 1) \frac{- 8 x}{\sqrt{4 - 4 x^{2}}} = 0 3 \sqrt{4 - 4 x^{2}} = 2 \Rightarrow x = 0, a n d x = \pm \frac{\sqrt{39}}{7} \Rightarrow y = \pm 2 \frac{\sqrt{10}}{7}$

يبين الشكل المجاور مستطيلًا مرسومًا داخل

مثلث قائم الزاوية. وهو متطابق الضلعين ، وطول قاعدته 2 وحدة طول :

5) أجد الإحداثي $y$ للنقطة $P$ بدلالة $x$ .

$S o l u t i o n : \frac{x - 1}{y - 0} = \frac{0 - 1}{1 - 0} y = 1 - x$

6) أكتب مساحة المستطيل بدلالة $x$ .

$S o l u t i o n : A = 2 x y = 2 x (1 - x) A (x) = 2 x - 2 x^{2}$

7) أجد أكبر مساحة مُمكنة للمستطيل.

$S o l u t i o n : A (x) = 2 x - 2 x^{2} A^{'} (x) = 2 - 4 x = 0 \Rightarrow x = \frac{1}{2}$

8) أجد أبعاد المستطيل.

$S o l u t i o n : w h e n x = \frac{1}{2} \Rightarrow y = 1 - \frac{1}{2} = \frac{1}{2}$

مثل الاقتران : $p = 150 - 0.5 x$ سعر البدلة الرجالية الذي حدٍّدته إحدى الشركات ،

حيث $x$ عدد البدلات المبيعة. ويُمثل الاقتران $C (x) = 4000 + 0.25 x^{2}$ تكلفة إنتاج البدلة:

9) أجد اقتران الإيراد.

الحل:

الإيراد = السعر × العدد

$p = 150 - 0.5 x R (x) = x (150 - 0.5 x) R (x) = 150 x - 0.5 x^{2}$

10) أجد اقتران الربح.

الحل:

$W (x) = R (x) - C (x) = 150 x - 0.5 x^{2} - 4000 - 0.25 x^{2} = 150 x - 0.75 x^{2} - 4000$

11) أجد عدد البدلات اللازم بيعها لتحقيق أكبر ربح مُمكن ، ثم أجد أكبر ربح مُمكن.

$S o l u t i o n : W (x) = 150 x - 0.75 x^{2} - 4000 W^{'} (x) = 150 - 1.5 x = 0 \Rightarrow x = \frac{150}{1.5} = 100$

باجراء اختبار المشتقة الثانية نجد أن :

$W^{''} (x) = - 1.5 \Rightarrow W^{''} (100) = - 1.5 < 0$

يوجد عند $x = 100$ قيمة عظمى مطلقة تجعل الربح أكبر ما يمكن .

12) أجد سعر البدلة الواحدة الذي يُحقَّق أعلى ربح مُمكن.

$S o l u t i o n : p (100) = 150 - 0.5 (100) = 100 J D$

13) تنتج مزرعة للتفّاح 30 صندوقًا من الشجرة الواحدة تقريبًا عند زراعة 20 شجرة في كل فدان من الأرض.

ويقل إنتاج الشجرة الواحدة بمقدار صندوق عند زراعة شجرة إضافية في كل فَدَانَ بسبب قرب الأشجار

الشديد بعضها من بعض. ما عدد الأشجار التى يجب زراعتها في كل فدََانَ لتحقيق أكبر إنتاج مُمكِن؟

الحل:

الانتاج = عدد الاشجار المزروعة × عدد الصناديق المنتجة

$I (x) = (30 - x) (20 + x) I (x) = 600 + 30 x - 20 x - x^{2} I (x) = 600 + 10 x - x^{2} I^{'} (x) = 10 - 2 x = 0 \Rightarrow x = 5$

باجراء اختبار المشتقة الثانية نجد أن :

$I^{''} (x) = - 2 I^{''} (5) = - 2 < 0$

يوجد عند $x = 5$ قيمة عظمى مطلقة تجعل الانتاج أكبر ما يمكن .

لدى مزارع $P$ مترًا طوليًّا من سياج ، يرغب في استعماله كاملا لتسييج حقل رَعي على شكل قطاع دائري ، زاويته $θ$ بالراديان. في دائرة نصف قُطْرها $r$ مترًا كما في الشكل المجاور:

14) أثبت أنَّ طول السياج اللازم إحاطة الحقل به هو: $P = r (θ + 2)$

الحل:

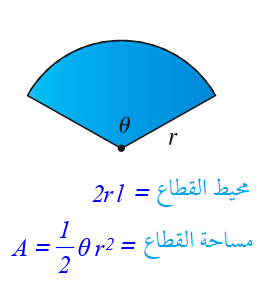طول السياج = محيط القطاع

$P = r + r + \overset{⏜}{l} = 2 r + \overset{⏜}{l} b u t \overset{⏜}{l} = r θ \Rightarrow P = 2 r + r θ = r (2 + θ)$

15) أثبت أنَّ مساحة القطاع هي: $A = \frac{1}{2} P r - r^{2}$

$S o l u t i o n : A = \frac{1}{2} θ r^{2} b u t P = r (θ + 2) \frac{P}{r} - 2 = θ \Rightarrow A = \frac{1}{2} θ r^{2} = \frac{1}{2} (\frac{P}{r} - 2) r^{2} \Rightarrow A = \frac{1}{2} P r - r^{2}$

16) أجد نصف قطْر القطاع بدلالة $P$ الذي تكون عنده مساحة الحقل أكبر ما يُمكن.

$S o l u t i o n : A (r) = \frac{1}{2} P r - r^{2} A^{'} (r) = \frac{1}{2} P - 2 r = 0 \Rightarrow r = \frac{P}{4}$

باجراء اختبار المشتقة الثانية نجد أن :

$A^{"} (r) = \frac{1}{2} P - 2 r A^{"} (\frac{P}{4}) = \frac{1}{2} P - 2 < 0$

يوجد عند $r = \frac{P}{4}$ قيمة عظمى مطلقة تجعل مساحة الحقل أكبر ما يمكن .

تقع النقطة $T$ على دائرة الوحدة التي معادلتها: $x^{2} + y^{2} = 1$ عند الزاوية $θ$ من المحور $x$ الموجب،

حيث: $0 \leq θ \leq \frac{π}{2}$ كما في الشكل المجاور:

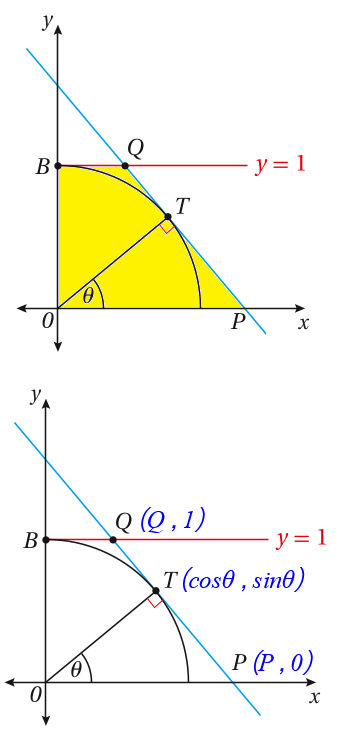17) أثبت أنَّ معادلة المستقيم $P T$ هي: $x c o s θ + y s i n θ = 1$ .

$S o l u t i o n : m = \frac{d}{d x} (x^{2} + y^{2} = 1) 2 x + 2 y \frac{d y}{d x} = 0 \Rightarrow \frac{d y}{d x} = - \frac{x}{y} y - y_{1} = m (x - x_{1}) f o r m = - \frac{x}{y} a t t h e p o i n t T b u t T = (c o s θ, s i n θ) y - s i n θ = - \frac{x}{y} (x - c o s θ) y^{2} - y s i n θ = - x^{2} + x c o s θ y^{2} + x^{2} = x c o s θ + y s i n θ b u t x^{2} + y^{2} = 1 x c o s θ + y s i n θ = 1$

18) أثبت أن مساحة شبه المُنحرف $O B Q P$ تعطى بالاقتران الآتي: $A = \frac{2 - s i n θ}{2 c o s θ}$ .

$S o l u t i o n : A = \frac{1}{2} (P + Q) b u t (P, 0) s a t i s f i e d t h e l i n e e q u a t i o n x c o s θ + y s i n θ = 1 \Rightarrow P c o s θ + (0) s i n θ = 1 \Rightarrow P = \frac{1}{c o s θ} a n d s o (Q, 1) s a t i s f i e d t h e l i n e e q u a t i o n x c o s θ + y s i n θ = 1 \Rightarrow Q c o s θ + (1) s i n θ = 1 \Rightarrow Q = \frac{1 - s i n θ}{c o s θ} \Rightarrow A = \frac{1}{2} (P + Q) = \frac{1}{2} (\frac{1}{c o s θ} + \frac{1 - s i n θ}{c o s θ}) \Rightarrow A = \frac{2 - s i n θ}{2 c o s θ}$

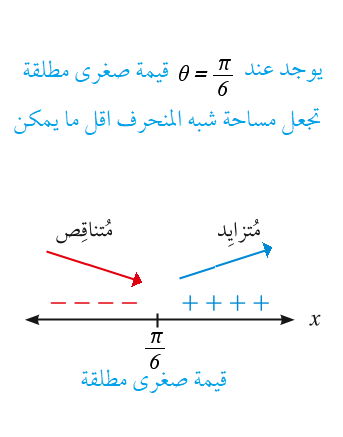
19) أجد قياس الزاوية $θ$ الذي تكون عنده مساحة شبه المُنحرف أقل ما يُمكن.

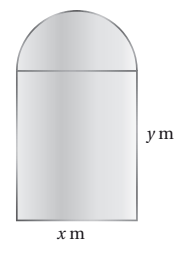$S o l u t i o n : A (θ) = \frac{2 - s i n θ}{2 c o s θ} A^{'} (θ) = \frac{- c o s θ (2 c o s θ) + 2 s i n θ (2 - s i n θ)}{4 c o s^{2} θ} = 0 - c o s θ (2 c o s θ) + 2 s i n θ (2 - s i n θ) = 0 - c o s^{2} θ + 2 s i n θ - s i n^{2} θ = 0; c o s^{2} θ + s i n^{2} θ = 1 - 1 + 2 s i n θ = 0 \Rightarrow s i n θ = \frac{1}{2} \Rightarrow θ = \frac{π}{6}$

20) يبين الشكل المجاور نافذة مُكوّنة من جزأين؛ أحدهما علوي على شكل نصف دائرة قُطرها $x m$ . والآخر سفلي على شكل مستطيل عرضه $x m$ ،

وارتفاعه $y m$ ، صُنْع الجزء العلوي من زجاج مُلوَّن يسمح بمرور 1وحدة ضوء لكل متر مربع ، وصُنْع الجزء السفلي من زجاج شفًاف يسمح بمرور 3 وحدات

ضوء لكل متر مربع. أجد قيمة كلّ من $x, y$ التي تجعل كمية الضوء المارَّ خلال النافذة أكبر ما يُمكن ، علمًا أن $10 m$ من المعدن الرقيق استعمل في تشكيل إطار

النافذة كاملًا بما في ذلك القطعة الفاصلة بين الجزأين.

$S o l u t i o n : l = π r f o r x = r \Rightarrow l = π \frac{x}{2} l + 2 x + 2 y = 10 π \frac{x}{2} + 2 x + 2 y = 10 \Rightarrow y = \frac{20 - (π + 4) x}{4} A = 1 A_{c i r c l e} + 3 A_{r e c a n g l e} = \frac{π}{8} x^{2} + x y = \frac{π}{8} x^{2} + 3 x (\frac{20 - (π + 4) x}{4}) A (x) = \frac{π}{8} x^{2} + 15 x - \frac{3 (π + 4) x^{2}}{4} A^{'} (x) = \frac{π}{4} x + 15 - \frac{3 (π + 4)}{2} x = 0 60 - 5 π x - 24 x = 0 \Rightarrow x = \frac{60}{5 π + 24}$

باجراء اختبار المشتقة الثانية نجد أن :

$A^{'} (x) = \frac{π}{4} x + 15 - \frac{3 (π + 4)}{2} x A'' (x) = \frac{π}{4} - \frac{3 (π + 4)}{2} = - \frac{π}{2} - 4 < 0$

يوجد عند $x = \frac{60}{5 π + 24}$ قيمة عظمى مطلقة تجعل كمية الضوء أكبر ما يمكن .

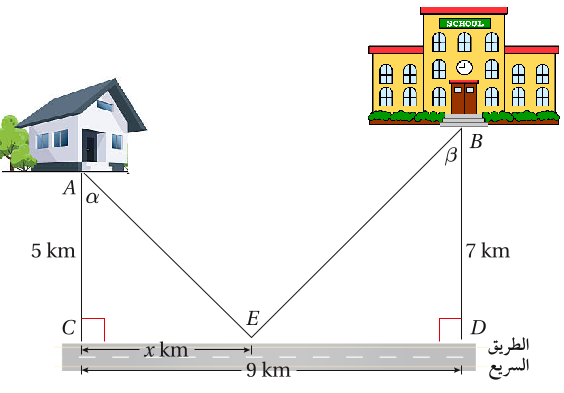يُمارس يوسف هواية ركوب الدرّاجات. وفي أحد الأيام ، انطلق على درّاجته من البيت

عند النقطة $A$ إلى المدرسة عند النقطة $B$ ماراً بالنقطة $E$ الواقعة على حافة الطريق السريع

كما في الشكل المجاور:

21) إذا كان الاقتران $L$ يمثل المسافة التي يقطعها . يوسف من البيت إلى المدرسة مرورا بالطريق السريع ، فأكتب $L$ بدلالة $x$

$S o l u t i o n : L = L_{1} + L_{2} L (x) = \sqrt{25 + x^{2}} + \sqrt{49 + {(9 - x)}^{2}}$

22) أثبت أنه إذا كان $\frac{d L}{d x} = 0$ فإن: $s i n α = s i n β$ .

$S o l u t i o n : L = L_{1} + L_{2} = \sqrt{25 + x^{2}} + \sqrt{49 + {(9 - x)}^{2}} \frac{d L}{d x} = \frac{2 x}{2 \sqrt{25 + x^{2}}} + \frac{- 2 (9 - x)}{2 \sqrt{49 + {(9 - x)}^{2}}} = 0 \Rightarrow \frac{x}{L_{1}} - \frac{9 - x}{L_{2}} = 0 \Rightarrow \frac{x}{L_{1}} = \frac{9 - x}{L_{2}} \Rightarrow s i n α = s i n β$

23) أجد قيمة $x$ التي تجعل المسافة التي يقطعها يوسف أقل ما يُمكِن.

$S o l u t i o n : L (x) = \sqrt{25 + x^{2}} + \sqrt{49 + {(9 - x)}^{2}} \frac{d L}{d x} = \frac{2 x}{2 \sqrt{25 + x^{2}}} + \frac{- 2 (9 - x)}{2 \sqrt{49 + {(9 - x)}^{2}}} = 0 \Rightarrow \frac{x}{L_{1}} - \frac{9 - x}{L_{2}} = 0 \Rightarrow \frac{x}{\sqrt{25 + x^{2}}} = \frac{9 - x}{\sqrt{49 + {(9 - x)}^{2}}} \Rightarrow \frac{x^{2}}{25 + x^{2}} = \frac{{(9 - x)}^{2}}{49 + {(9 - x)}^{2}} 8 x^{2} + 125 x - 675 = 0 x = \frac{- 125 \pm \sqrt{{(125)}^{2} + 4 (8) (675)}}{2 (8)} = \frac{- 125 \pm \sqrt{37225}}{16} \approx \frac{- 125 \pm 290.98}{16} \Rightarrow x = \frac{165.98}{16}$

وبإجراء اختبار المشتقة الأولى :

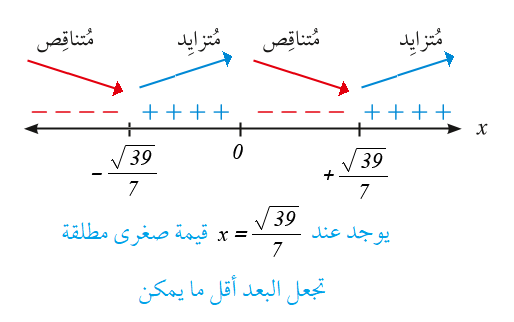
يوجد عند $x = \frac{165.98}{16}$ قيمة صغرى مطلقة تجعل المسافة المقطوعة أقل ما يمكن .

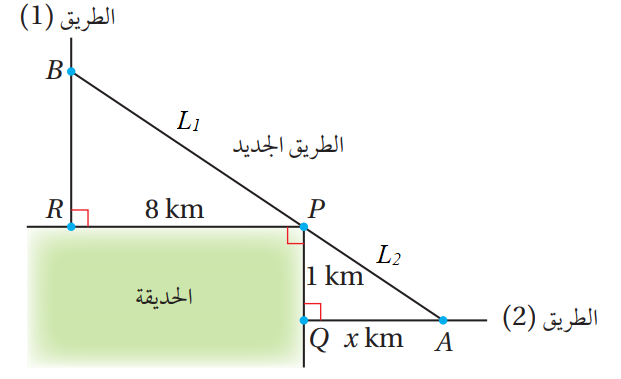24) يمثل الشكل المجاور مدخلين لحديقة عامة عند الطريق النقطة $R$ والنقطة $Q$ ، ويُمكِن الوصول إلى هذين المدخلين من طريقين

عموديين على ضلعي الحديقة. أرادت البلدية إنشاء طريق جديد يصل بين الطريقين القديمين ، ويمرّ بالنقطة $P$ التي تُمثّل زاوية الحديقة ،

فاختارت النقطة $A$ والنقطة $B$ على الطريقين ليكون طول الطريق الجديد أقصر مايُمكن. علمًا أن النقطة $A$ تقع على بُعْد $x k m$ من النقطة

أجد قيمة $x$ التي تجعل طول الطريق الجديد أقصر ما يُمكن.

$S o l u t i o n : L = L_{1} + L_{2} = \sqrt{1 + x^{2}} + \sqrt{64 + y^{2}} T o f i n d y t a n A = t a n P \frac{1}{x} = \frac{y}{8} \Rightarrow y = \frac{8}{x} L (x) = \sqrt{1 + x^{2}} + \sqrt{64 + {(\frac{8}{x})}^{2}} = \sqrt{1 + x^{2}} + \sqrt{64 + \frac{64}{x^{2}}} L (x) = \sqrt{1 + x^{2}} + 8 \sqrt{1 + \frac{1}{x^{2}}} L' (x) = \frac{2 x}{2 \sqrt{1 + x^{2}}} + 8 \times \frac{\frac{- 2}{x^{3}}}{2 \sqrt{1 + \frac{1}{x^{2}}}} = 0 \frac{x}{\sqrt{1 + x^{2}}} + \frac{- 8}{x^{3} \sqrt{1 + \frac{1}{x^{2}}}} = 0 \Rightarrow x^{3} = 8 \Rightarrow x = 2$

وبإجراء اختبار المشتقة الأولى :

يوجد عند $x = 2$ قيمة عظمى مطلقة تجعل طول الطريق أقصر ما يمكن .

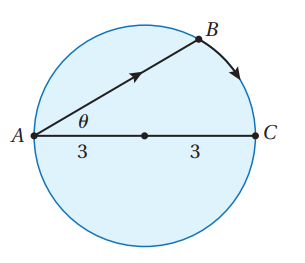25) تبرير: يقف رجل عند النقطة على شاطئ بحيرة دائرية نصف قُطْرها $3 k m$ وهو يريد الوصول إلى النقطة المقابلة تمامًا للنقطة ‎ على الجانب الآخر

من البحيرة ، في أقصر وقت مُمكِن كما في الشكل المجاور. يُمكن للرجل أن يُجِدِف بزورق من النقطة $A$ إلى النقطة $B$ بسرعة $3 k m / h$ .

ثم يركض حول حافة البحيرة بسرعة $6 k m / h$ . أحدّد موقع النقطة ليصل الرجل من النقطة $A$ إلى النقطة $C$ في أقل وقت مُمكن؟ أبرّر إجابتي.

السرعة عبر المسار $A B$ تساوي $3 k m / h$ .بالتالي فإنّ الزمن عبر هذا المسار يساوي $T_{1} = \frac{A B}{3}$

السرعة عبر القوس $B C$ تساوي $6 k m / h$ . بالتالي فإنّ الزمن عبر هذا المسار يساوي $T_{2} = \frac{\overset{⏜}{B C}}{6}$

كذلك فإن قياس الزاوية $π - 2 θ = A O B$ زوايا متساوي الساقين

قياس الزاوية $2 θ = B O C$ زاوية خارجة

$C O = B O = A O = 3 k m$ أنصاف اقطار

$A b = \sqrt{{(3)}^{2} + {(3)}^{2} - 2 (3) (3) c o s (π - 2 θ)} = 3 \sqrt{2} . \sqrt{1 - c o s (π - 2 θ)} = 3 \sqrt{2} . \sqrt{2 c o s^{2} θ} = 6 c o s θ; 0 \leq θ \leq \frac{π}{2}$

كذلك طول القوس الأصغر $B C$

$L = r (2 θ) = 6 θ$

المطلوب : القيمة الصغرى للزمن الكلي
$T = t_{1} + t_{2} = \frac{A B}{3} + \frac{L}{6} = \frac{6 c o s θ}{3} + \frac{6 θ}{6} T (θ) = 2 c o s θ + θ T^{'} (θ) = - 2 s i n θ + 1 = 0 \Rightarrow s i n θ = \frac{1}{2} \Rightarrow θ = \frac{π}{6} h$

وبإجراء اختبار المشتقة الثانية : $T^{'} (θ) = - 2 s i n θ + 1 T^{''} (θ) = - 2 c o s θ T^{''} (\frac{π}{6}) = - 2 c o s (\frac{π}{6}) = - 2 \times \frac{\sqrt{3}}{2} = - \sqrt{3}$

يوجد عند $θ = \frac{π}{6} h$ قيمة عظمى مطلقة تجعل الوقت أقل ما يمكن .

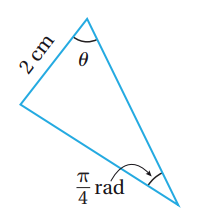تحدّ: يُبيّن الشكل المجاور مثلثاً، قياس إحدى زواياه $\frac{π}{4} r a d$ ، ومقابلها ضلع طوله $2 c m$

26) أثبت أن مساحة المثلث $A$ تُعطى بالاقتران $A = s i n 2 θ - c o s 2 θ + 1$

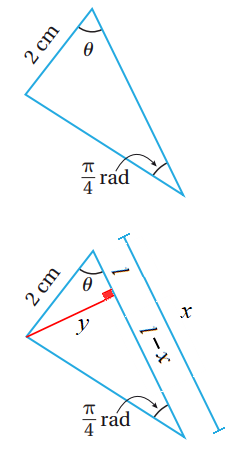من الشكل نجد أن مساحة المثلث $A = \frac{1}{2} x y$ والمطلوب حل قيمتي $x, y$ بدلالة $θ$ :

$s i n θ = \frac{y}{2} \Rightarrow y = 2 s i n θ A = \frac{1}{2} x y = \frac{1}{2} x (2 s i n θ) A = x s i n θ \dots 1 t a n (\frac{π}{4}) = \frac{y}{x - l} 1 = \frac{y}{x - l} \Rightarrow x = l + y x = l + 2 s i n θ c o s θ = \frac{l}{2} \Rightarrow l = 2 c o s θ \Rightarrow x = l + 2 s i n θ x = 2 c o s θ + 2 s i n θ \dots 2$

وبحل المعادلتين نجد أن:

$A = x s i n θ \dots 1 x = 2 c o s θ + 2 s i n θ \dots 2 A = (2 c o s θ + 2 s i n θ) s i n θ = 2 c o s θ s i n θ + 2 s i n^{2} θ = s i n 2 θ - c o s 2 θ + 1; 2 c o s θ s i n θ = s i n 2 θ; c o s 2 θ = 1 - 2 s i n^{2} θ$

27) أجد مجال الاقتران في السؤال السابق.

$A = 2 c o s θ s i n θ + 2 s i n^{2} θ > 0 l e t 2 c o s θ s i n θ + 2 s i n^{2} θ = 0 2 s i n θ (c o s θ + s i n θ) = 0 2 s i n θ = 0 \Leftrightarrow θ = 0, π r e j e c t e d c o s θ + s i n θ = 0 c o s θ = - s i n θ \Rightarrow t a n θ = - 1 \Leftrightarrow θ = \frac{3 π}{4}$

مجال الاقتران $(0, \frac{3 π}{4})$

28) أثبت أن أكبر مساحة ممكنه للمثلث هي : $(1 + \sqrt{2}) c m^{2}$

$S o l u t i o n : A (θ) = s i n 2 θ - c o s 2 θ + 1 A^{'} (θ) = 2 c o s 2 θ + 2 s i n 2 θ = 0 c o s 2 θ + s i n 2 θ = 0 s i n 2 θ = - c o s 2 θ t a n 2 θ = - 1 \Rightarrow 2 θ = \frac{3 π}{4} \Rightarrow θ = \frac{3 π}{8} A^{''} (θ) = - 4 s i n 2 θ + 4 c o s 2 θ A^{''} (\frac{3 π}{8}) = - 4 s i n 2 (\frac{3 π}{8}) + 4 c o s 2 (\frac{3 π}{8}) = (- \frac{8}{\sqrt{2}})$

بالتعويض

$A (θ) = s i n 2 (\frac{3 π}{8}) - c o s 2 (\frac{3 π}{8}) + 1 A (θ) = s i n (\frac{3 π}{4}) - c o s (\frac{3 π}{4}) + 1 = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} + 1 = \frac{2}{\sqrt{2}} + 1 = (\sqrt{2} + 1) c m^{2}$

رياضيات فصل أول

التوجيهي علمي

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS