رياضيات فصل ثاني

تقدير ميل المنحنى 

تعلمنا في الصف التاسع كيفية حساب ميل الخط المستقيم الذي يساوي ناتج قسمة الفرق بين إحداثي المحور y  على الفرق بين إحداثي محور x. 

---

• سوف نتعلم في هذا الدرس كيفية إيجاد ميل منحنى ليس مستقيمًا .
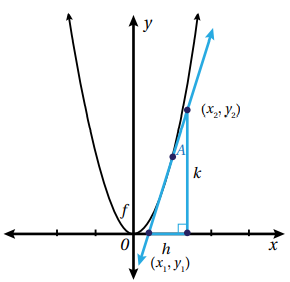
• إن ميل المنحنى عند نقطة واقعة عليه يساوي ميل المماس عند تلك النقطة؛ لذا فإن ميل المنحنى يختلف من نقطة لأخرى عليه .

• لإيجاد ميل المنحنى عند نقطةٍ ما نرسم مماسا عند تلك النقطة ثم نجد ميل المماس باستخدام إحداثيات نقطتين عليه 

$\left(x_2 , y_2\right) و \left(x_{1 } , y_1\right)$, وذلك بالتعويض بصيغة ميل المستقيم $m =\frac{y_2 - y_1}{x_2 - x_1} = \frac{k }{h}$ حيث $x_2 - x_1 \ne y_2 - y_1$

مثال 1:

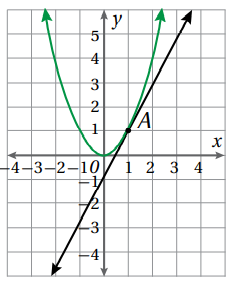
يمثل المستقيم في الشكل المجاور مماسا لمنحنى الاقتران  y = x²  عند النقطة  A( 1, 1)  .

أجد ميل منحنى الاقتران عند النقطة A.

الحل :

أحدد نقطتين على المماس من الرسم : $B \left(0, -1\right)$ و $C\left(2 , 3\right)$ثم أحسب الميل:

صيغة الميل                                                                                   $m =\frac{y_2 - y_1}{x_2 - x_1}$

 

وبالتعويض                                                                                     $= \frac{3-(-1)}{2- 0}$

 

بالتبسيط                                                                                                        2 = 

إذا ميل منحنى الاقتران عند النقطة A  هو 2

---

• إذا لم يكن المماس مرسوما عند النقطة التي يراد إيجاد ميل المنحنى عندها ، فإنه يرسم باستعمال المسطرة . وبما أن الرسم اليدوي ليس دقيقًا ، فإن ميل المماس المرسوم قد يختلف قليلا عن القيمة الدقيقة لميل المنحنى ، عندئذ يكون الناتج قيمة تقريبية لميل المنحنى .

 

مثال 2

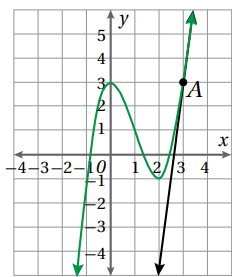
أقدر ميل منحنى الاقتران  y = x³ - 2x² +3  عند كل نقطة مما يأتي :

1. النقطة A (3, 3) 

الخطوة الأولى : 

أرسم مماسا للمنحنى عند النقطة A (3, 3) باستعمال المسطرة .

الخطوة الثانية:

أحدد نقطتين على المماس C (2, -5)   و A (3, 3)  ثم أجد الميل .

$m =\frac{y_2 -y_1}{x_2 - x_1}= \frac{-5 -3 }{2- 3}= 8$

إذا ميل منحنى الاقتران عند النقطة A هو 8 تقريبًا .

 

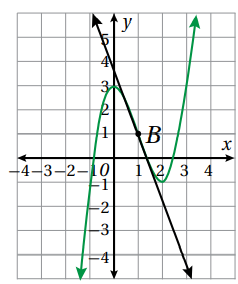
2. النقطة  ( 1, 1) B

أرسم مماسا عند النقطة B ، ثم أحدد نقطتين عليه $E \left(0 , 3.8\right)$ , $B \left(1 , 1\right)$ ثم أجد الميل :

$m =\frac{y_2- y_1}{x_2 - x_1} = \frac{1 -3.8 }{1- 0}= -2.8$

إذا ميل منحنى الاقتران عند النقطة B هو 2.8 -

 

3.  أكتب معادلة المماس المار بالنقطة  ( 1, 1) B

معادلة المماس                                               

                                                    y - b = m( x -a)

بتعويض النقطة B (1,1)  و m = -2.8   

y - 1 = -2.8 ( x -1)

y = 3.8 - 2.8 x

---

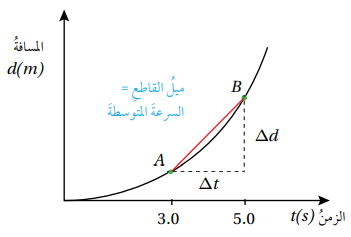
•  تعرفت سابقا أن منحنى المسافة - الزمن يكون مستقيما عند الحركة بسرعة ثابتة ، وأنه لا يكون مستقيما عند الحركة بسرعة متغيرة .
• تعرفت أيضا كيفية حساب السرعة المتوسطة  $\frac{}{V}$ لجسم متحرك في فترة زمنية ، وذلك بتقسيم التغير في المسافة $∆s$  على التغير في الزمن $∆t$ :

$v_{a}g=\overline{v}=\frac{\Delta s}{\Delta t}$

توضيح 

بالنظر إلى منحنى المسافة - الزمن في الأسفل ، يتبين أن السرعة للسيارة من الثانية الثالثة إلى الثانية الخامسة تساوي ميل القاطع الذي يمر بالنقطتين  A و B  على المنحنى .

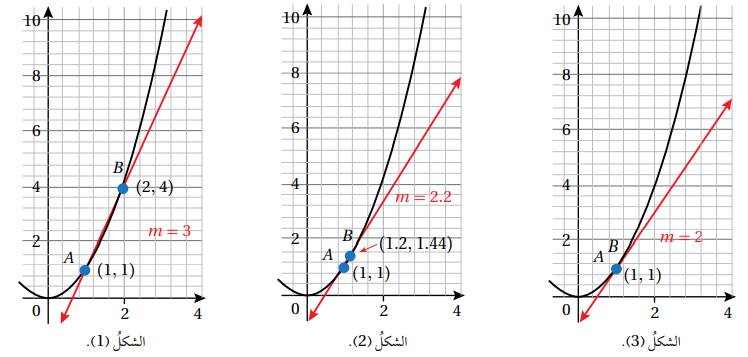
• لكن السرعة المتوسطة لا تقدم معلومات كافية في كثير من المواقف ، مثل تحديد سرعة سيارة لحظة مرورها أمام الرادار ؛ فتلوم عندئذ السرعة اللحظية التي يمكن إيجادها بتقليص الفترة الزمنية للسرعة المتوسطة حتى تصبح نقطة ( لحظة) كما في الأشكال التالية ، فيصبح القاطع الذي يمر بنقطتين على المنحنى مماسًا له عند نقطة واحدة.

بما أن ميل المماس يساوي ميل المنحنى عند نقطة التماس ، فإن السرعة اللحظية عند لحظة ما تساوي ميل منحنى المسافة -  الزمن عند تلك اللحظة .

---

   مثال 3   

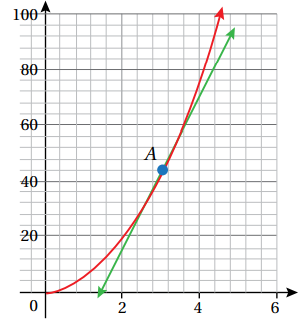
يمثل الاقتران $d\left(t\right) = 4.9 t^{ 2}$ العلاقة بين المسافة المقطوعة d بالمتر والزمن t بالثانية ( منحنى المسافة - الزمن ) لكرة تسقط سقوطا حرا من وضع السكون . أجد سرعة الكرة بعد 3 ثوانٍ من سقوطها .

الحل 

نعوض  t = 3  بالاقتران 

نتتج النقطة A ( 3 , 44.1 )  

A  هي نقطة التماس 

نمثل بيانيا  منحنى الاقتران 

d(t) = 4.9 t²

ونرسم المماس عند النقطة

A ( 3 , 44.1 ) 

نحدد نقطتين على المماس  A ( 3 , 44.1 )  و  B ( 2 ,16)  ثم استعملها لحساب الميل .

$m = \frac{y_2 - y_1}{x_2 - x_1} =\frac{44.1 - 16}{3 -2} = 28.1$ 

إذا ، ميل منحنى الاقتران عند النقطة A ( 3 , 44.1 )  هو 28.1 تقريبًا . ومنه ، فإن سرعة الكرة اللحظية بعد 3 ثوانٍ هي  28.1m/s .

---