رياضيات 10 فصل ثاني

أتحقق من فهمي صفحة 57

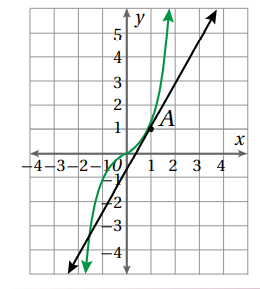
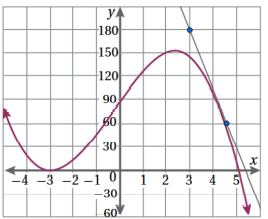
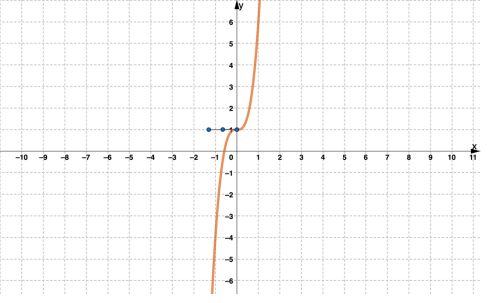
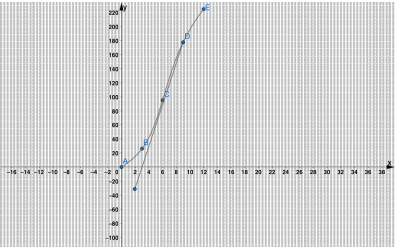
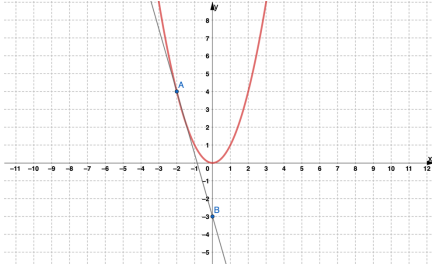
يمثل المستقيم في الشكل المجاور مماسا لمنحنى الاقتران y =x³  عند النقطة  (A (1 ,1  

أجد ميل منحنى الاقتران عند النقطة

$(1,1),(2,4)$

$m=\frac{4-1}{2-1}=\frac{3}{1}=3$

---

 

أتحقق من فهمي صفحة 58 

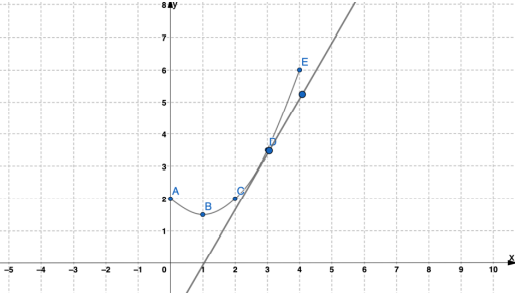
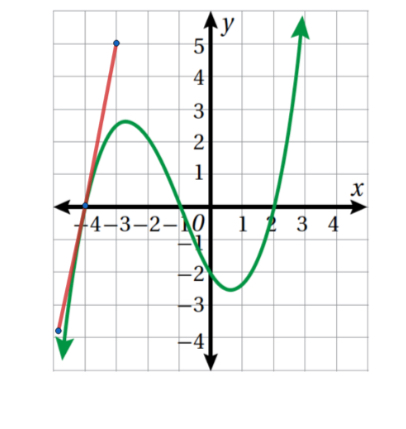
أقدر ميل منحنى الاقتران الممثل بيانيا في الشكل المجاور عند كل من النقطتين : $A(-4,0) , B(0,-2)$

الميل عند  (  2- , 0 )

$(0,-2),(-3,2)\Rightarrow m=\frac{2--2}{-3-0}=\frac{4}{-3}$

كما يوجد حلول متعددة 

برسم خط مستقيم مار بالنقطة ( 2 , 3-) 

( تقيل الإجابات القريبة من هذا الجواب ) 
 

الميل عند  (0, 4-) 

$(-4,0),(-3,5)\Rightarrow m=\frac{5-0}{-3--4}=\frac{5}{1}=5$

---

 

أتحقق من فهمي صفحة  60

 

يمثل الاقتران  $d\left(t\right)=t^{ 2}+t$  المسافة التي يقطعها جسم ما، حيث d المسافة المقطوعة بالمتر ، و t الزمن بالثانية  . أقدر السرعة اللحظية بعد 5 توانٍ ، و 11 ثانية.

 d(5) = 25 +5 =30

$(5,30),(6,41)\Rightarrow m=\frac{41-30}{6-5}=\frac{11}{1}=11$
 

$d\left(11\right)=121+11=132$

$(11,132),(6,18)\Rightarrow m=\frac{132-18}{11-6}=\frac{114}{5}=22.8$


 

---

 

أتدرب وأحل المسائل 

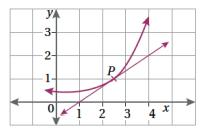
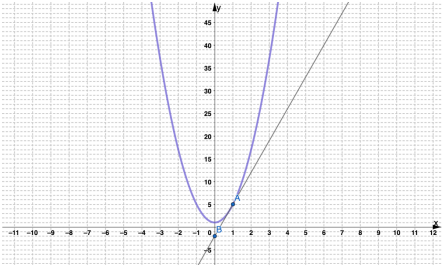
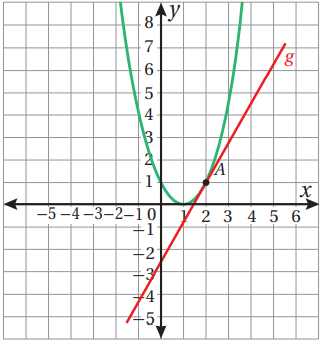
1. يمثل المستقيم في الشكل المجاور مماسا لمنحنى اقتران عند النقطة  (P (2.5, 1  . أجد ميل منحنى الاقتران عند النقطة P

( 2.5 , 1) , ( 4,2)

 

$m =\frac{2-1}{4-2.5}= \frac{1}{1.5}= 0.66$

---

 

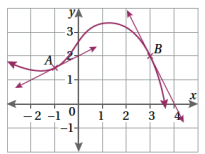
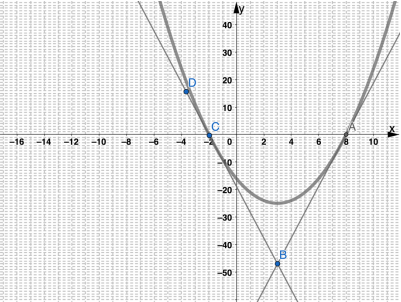
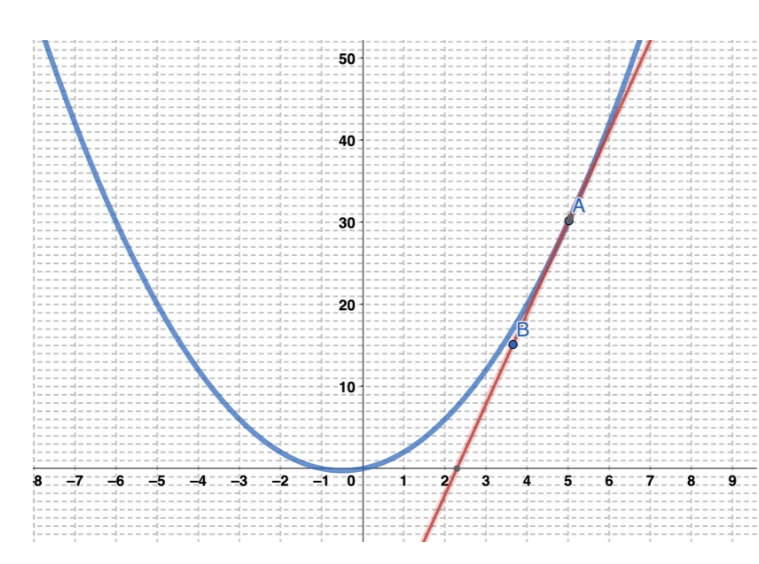
2. في الشكل المجاور، رسم مماسان لمنحنى اقتران عند النقطتين  $A \left(-1 , 1.5\right)$ و $B \left(3 ,2 \right)$ 

أجد ميل منحنى الاقتران عند كل من A و B 

$\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{5}\mathbf{)}\mathbf{,}\mathbf{(}\mathbf{ }\mathbf{0}\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{2}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{.}\mathbf{5}}{\mathbf{0}\mathbf{-}\mathbf{-}\mathbf{1}}\mathbf{=}\frac{\mathbf{0}\mathbf{.}\mathbf{5}}{\mathbf{1}}\mathbf{=}\mathbf{0}\mathbf{.}\mathbf{5}$

$\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{,}\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{(}\mathbf{4}\mathbf{.}\mathbf{0}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{0}\mathbf{-}\mathbf{2}}{\mathbf{4}\mathbf{-}\mathbf{3}}\mathbf{=}\frac{\mathbf{-}\mathbf{2}}{\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{2}\mathbf{ }$

---

 

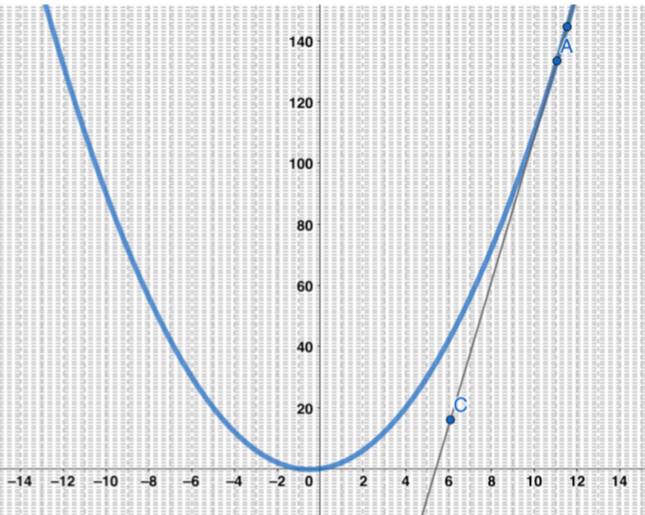
3. أقدر ميل منحنى الاقتران المبين جانبًا عند النقطة  $\left( 2 , 150\right)$ والنقطة $\left( 4.5 , 60\right)$. 

الحل : 

$\mathbf{(}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{150}\mathbf{)}\mathbf{ }\mathbf{,}\mathbf{(}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{120}\mathbf{)}\mathbf{\Rightarrow }\mathit{m}\mathbf{=}\frac{\mathbf{150}\mathbf{-}\mathbf{120}}{\mathbf{2}\mathbf{-}\mathbf{0}}\mathbf{=}\frac{\mathbf{30}}{\mathbf{2}}\mathbf{=}\mathbf{15}$

 

$\mathbf{(}\mathbf{4}\mathbf{.}\mathbf{5}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{60}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{180}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{180}\mathbf{-}\mathbf{60}}{\mathbf{3}\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}}\mathbf{=}\frac{\mathbf{120}}{\mathbf{-}\mathbf{1}\mathbf{.}\mathbf{5}}\mathbf{=}\mathbf{-}\mathbf{80}\mathbf{ }$

---

 

استعمل جدول القيم الآتي للإجابة عن الأسئلة $\left( 4 - 7\right)$

X	0	1	2	3	4
F(x)	2	1.5	2	3.5	6

 

4. أمثل منحنى الاقتران $f\left(x\right)$  بيانيًا في الفترة $0 \le x \le 4$

5 . أرسم مماسا لمنحنى الاقتران عند النقطة $(3,3.5)$ .

6. أقدر ميل منحنى الاقتران عند النقطة  $(3,3.5)$ .

7. ما إحداثيات النقطة التي يكون ميل المنحنى عندها صفرًا ؟

$\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{5}\mathbf{)}\mathbf{,}\mathbf{(}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{3}\mathbf{.}\mathbf{5}\mathbf{ }\mathbf{-}\mathbf{0}}{\mathbf{3}\mathbf{-}\mathbf{1}}\mathbf{=}\frac{\mathbf{3}\mathbf{.}\mathbf{5}}{\mathbf{2}}\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{75}$

الميل يساوي 0 عند  (1.5 , 1)  لأن الميل عندا أفقي 

---

 

أكمل جدول قيم الاقتران $f\left(x\right) = 0.1 x^3$ الآتي، ثم استعمله لحل المسائل  $\left( 8 - 10 \right)$

X	0	0.5	1	1.5	2	2.5	3
F(x)		0.01	0.1		0.8

 

8.  أرسم منحنى الاقتران $f\left(x\right) = 0.1 x^3$  في الفترة $0 \le x\le 3$

9.  أرسم مماسا لمنحنى الاقتران عند النقطة $(2,0.8)$.

10. أقدر ميل منحنى الاقتران عند النقطة $(2 , 0.8)$

الحل : 

X	0	0.5	1	1.5	2	2.5	3
F(x)	0	0.01	0.1	0.3	0.8	1.6	2.7

 

$\mathbf{(}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{8}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{\Rightarrow }\mathit{m}\mathbf{=}\frac{\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{8}}{\mathbf{0}\mathbf{-}\mathbf{2}}\mathbf{=}\frac{\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{8}}{\mathbf{-}\mathbf{2}}\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{4}$

 

---

 

أقدر ميل منحنى كل اقتران مما يأتي :

11. $y=4x^{2 }+1$  عند النقطة $(1,5)$

الحل :

$\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{5}\mathbf{)}\mathbf{,}\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{5}\mathbf{)}\mathbf{\Rightarrow }\mathit{m}\mathbf{=}\mathbf{ }\frac{\mathbf{5}\mathbf{-}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{5}}{\mathbf{1}\mathbf{-}\mathbf{0}}\mathbf{=}\frac{\mathbf{7}\mathbf{.}\mathbf{5}}{\mathbf{1}}\mathbf{=}\mathbf{7}\mathbf{.}\mathbf{5}\mathbf{ }$

 

12. $y =3 + 2 x^2$  عند  النقطة $(-1,5)$

الحل

 

$\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{5}\mathbf{)}\mathbf{،}\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{)}\mathbf{\Rightarrow }\mathit{m}\mathbf{=}\frac{\mathbf{5}\mathbf{-}\mathbf{1}}{\mathbf{-}\mathbf{1}\mathbf{ }\mathbf{-}\mathbf{0}}\mathbf{=}\frac{\mathbf{4}}{\mathbf{-}\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{4}$

 

13. $y = 1- x^2$ عند النقطة $(-1,0)$

( -1 , 0) ( 0,2)

$\mathit{m}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{2}\mathbf{-}\mathbf{0}}{\mathbf{0}\mathbf{-}\mathbf{-}\mathbf{1}}\mathbf{=}\mathbf{ }\frac{\mathbf{2}}{\mathbf{1}}\mathbf{=}\mathbf{ }\mathbf{2}$

14. $y = 5x^3 + 1$ عند النقطة $( 0,1)$

الميل 0 لأن المماس أفقي 

15. $y = 9 - x^2$  عند النقطة $(2,5)$

الحل :

( 2 ,5) ( 4 , -2)

$\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{5}\mathbf{)}\mathbf{,}\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{\Rightarrow }\mathit{m}\mathbf{=}\frac{\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{-}\mathbf{5}}{\mathbf{4}\mathbf{-}\mathbf{2}}\mathbf{=}\frac{\mathbf{-}\mathbf{7}}{\mathbf{2}}\mathbf{=}\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{5}$

 

16.  $y = 8- 2x$ عند النقطة $(1,6)$

$\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{6}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{ }\mathbf{8}\mathbf{)}\mathbf{\Rightarrow }\mathit{m}\mathbf{=}\frac{\mathbf{8}\mathbf{-}\mathbf{6}}{\mathbf{0}\mathbf{-}\mathbf{1}}\mathbf{=}\frac{\mathbf{2}}{\mathbf{-}\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{ }\mathbf{2}\mathbf{ }$

---

 

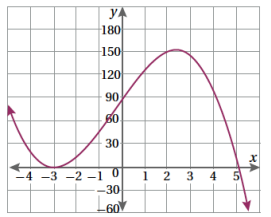
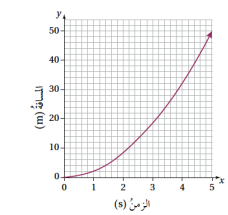
دراجات نارية بدأت دراجة نارية الحركة من وضع السكون في مسار مستقيم . ويبين المنحنى المجاور المسافة التي قطعتها الدراجة في 5 ثوانٍ:

17.  أرسم نسخة من المنحنى ، مستعينًا بالجدول الآتي:

X	0	1	2	3	4	5
F(x)	0	2	8	18	32	50

18. أرسم مماسا للمنحنى عندما  t = 2 
19 .أقدر سرعة الدراجة بعد ثانيتين 

20 . أقدر سرعة الدراجة بعد 4 ثوانٍ من بدء الحركة.

21. أحسبُ السرعةَ المتوسّطةَ للدراجةِ في الفترةِ الزمنيَّةِ [1,3].

الحل 

السرعة بعد 2 ثانية 

$\mathbf{(}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{8}\mathbf{)}\mathbf{،}\mathbf{ }\mathbf{(}\mathbf{1}\mathbf{.}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{8}\mathbf{-}\mathbf{0}}{\mathbf{2}\mathbf{-}\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{1}\mathbf{ }}\mathbf{=}\frac{\mathbf{8}}{\mathbf{0}\mathbf{.}\mathbf{9}}\mathbf{\approx }\mathbf{8}\mathbf{.}\mathbf{9}$

 

 

السرعة بعد 4 ثانية 

$\mathbf{(}\mathbf{4}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{32}\mathbf{)}\mathbf{ }\mathbf{،}\mathbf{(}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{32}\mathbf{ }\mathbf{-}\mathbf{0}}{\mathbf{4}\mathbf{-}\mathbf{2}}\mathbf{=}\frac{\mathbf{32}}{\mathbf{2}}\mathbf{=}\mathbf{16}$

السرعةَ المتوسّطةَ للدراجةِ في الفترةِ الزمنيَّةِ [1,3]. 8m/s

---

 

سيارات:  أراد مهندس أن يدرس سرعة سيارة ، فسجل المسافة المقطوعة كل 3 ثوانٍ كما في الجدول الآتي ، ثم استعمل المعادلة $x = a{t}^{ 2} + b{t}^{ 4}$  لتمثيل العلاقة بين قيم المسافة والزمن، حيث a وb  عددان ثابتان:

الزمن (الثانية)	0	3	6	9	12
المسافة x ( متر)	0	26.19	95.04	177.39	224.64

 

22. أرسم منحنى المسافة - الزمن .

23.  أقدر السرعة عندما t =3 

24. أجد قيمة كل من : a و b 

الحل

 

 

---

 

فيزياء : تمثل المعادلة  $s\left(t\right)=3t - t^{ 2}$ المسافة التي يقطعها جسم المتر ، حيث t الزمن بالثانية .أقدر سرعة الجسم عندما t = 2 

الحل :

السرعة بعد 2 ثانية 

$\mathbf{(}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{،}\mathbf{ }\mathbf{(}\mathbf{4}\mathbf{ }\mathbf{,}\mathbf{0}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{0}\mathbf{-}\mathbf{ }\mathbf{2}}{\mathbf{4}\mathbf{ }\mathbf{-}\mathbf{2}}\mathbf{=}\mathbf{-}\frac{\mathbf{2}}{\mathbf{2}}\mathbf{=}\mathbf{-}\mathbf{1}\mathbf{ }$

 

---

 

مهارات التفكير العليا 

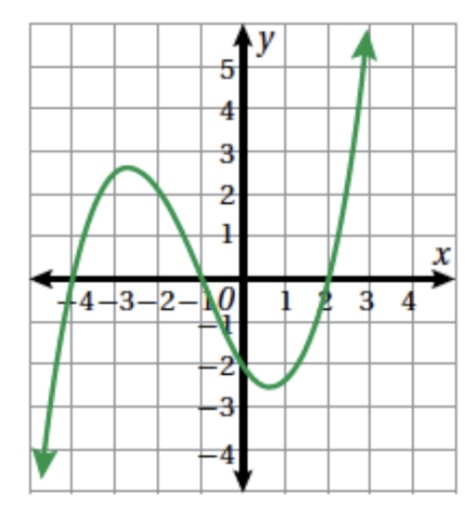
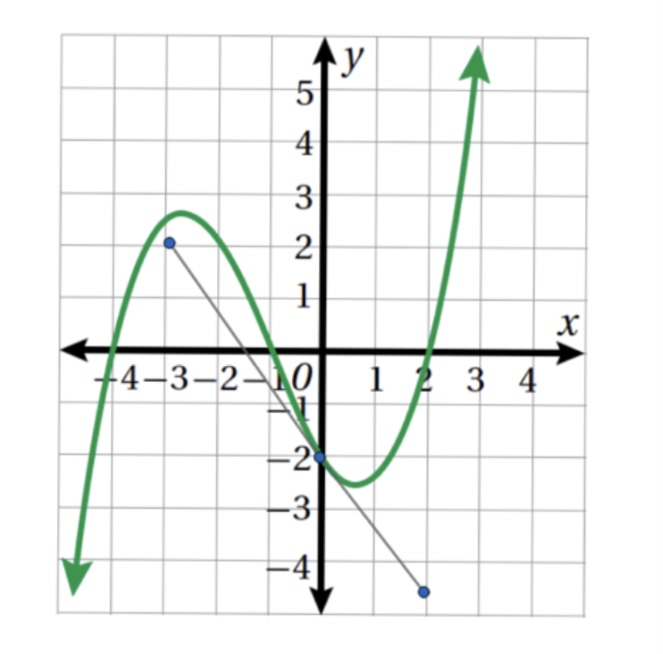
25 . تبرير. أقدر ميل منحنى الاقتران   $f\left(x\right)=x^{ 2 } - 6x-16$ عند كل من النقاط الآتية  مبررًا إجابتي :  

•  نقطتا تقاطع المنحنى مع المحور x
•  نقطة تقاطع المنحنى مع محور y 

الحل

 

نقطتا التقاطع مع محور  x

$\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{0}\mathbf{)}\mathbf{ }\mathbf{،}\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{,}\mathbf{-}\mathbf{47}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{-}\mathbf{47}\mathbf{ }\mathbf{-}\mathbf{0}}{\mathbf{3}\mathbf{-}\mathbf{8}}\mathbf{=}\frac{\mathbf{-}\mathbf{47}}{\mathbf{5}}\mathbf{\approx }\mathbf{-}\mathbf{9}\mathbf{.}\mathbf{4}$

$\mathbf{(}\mathbf{8}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\mathbf{،}\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{47}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{-}\mathbf{47}\mathbf{-}\mathbf{0}}{\mathbf{3}\mathbf{-}\mathbf{8}}\mathbf{=}\frac{\mathbf{-}\mathbf{47}\mathbf{ }}{\mathbf{-}\mathbf{5}\mathbf{ }}\mathbf{\approx }\mathbf{ }\mathbf{9}\mathbf{.}\mathbf{4}$

نقطتا التقاطع مع المحور y 

$\mathbf{(}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{16}\mathbf{)}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{.}\mathbf{6}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{-}\mathbf{16}\mathbf{ }\mathbf{-}\mathbf{0}}{\mathbf{0}\mathbf{-}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{6}}\mathbf{=}\frac{\mathbf{-}\mathbf{16}}{\mathbf{2}\mathbf{.}\mathbf{6}}\mathbf{\approx }\mathbf{-}\mathbf{6}\mathbf{.}\mathbf{2}$

---

 

26 .مسألة مفتوحة : اكتب قاعدة اقتران من الدرجة  الثانية ، ثم أمثله بيانيًا ، مقدرا ميله عند نقطتين متعاكستين عليه. $( -a , b)$ , $(a , b)$

الحل 

* حل مقترح 

$f\left(x\right)=x^2$

^.

^{$\mathbf{(}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{4}\mathbf{)}\mathbf{،}\mathbf{ }\mathbf{(}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{3}\mathbf{)}\Rightarrow \mathit{m}\mathbf{ }\mathbf{=}\frac{\mathbf{4}\mathbf{-}\mathbf{-}\mathbf{3}}{\mathbf{2}\mathbf{-}\mathbf{0}}\mathbf{=}\frac{\mathbf{7}}{\mathbf{2}}\mathbf{ }\mathbf{\approx }\mathbf{3}\mathbf{.}\mathbf{5}$}

 

^{$\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{,}\mathbf{4}\mathbf{)}\mathbf{،}\mathbf{ }\mathbf{(}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{3}\mathbf{)}\Rightarrow \mathit{m}\mathbf{=}\frac{\mathbf{4}\mathbf{-}\mathbf{-}\mathbf{3}}{\mathbf{-}\mathbf{2}\mathbf{-}\mathbf{0}}\mathbf{=}\frac{\mathbf{7}}{\mathbf{-}\mathbf{2}}\mathbf{\approx }\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{5}\mathbf{ }$}

 

---

 

كتاب التمارين

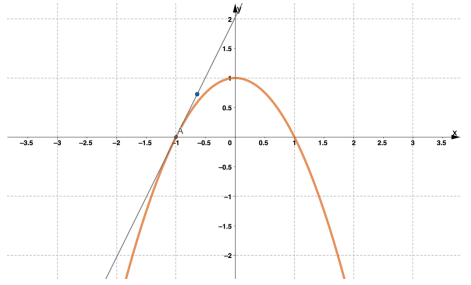
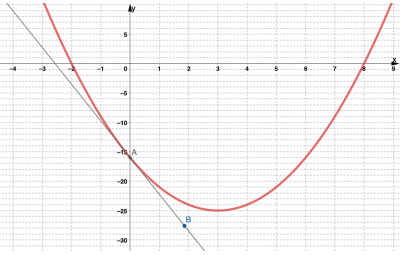
1. يمثل المستقيم في الشكل المجاور مماسا لمنحنى الاقتران  y = x² - 3x +4  عند النقطة A( 0 , 4) . أقدر ميل منحنى الاقتران عند النقطة A. 

الحل

m = - 2.6 

---

 

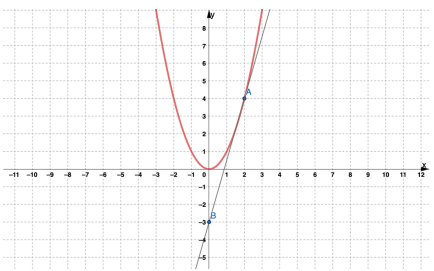
2. يمثل المستقيم في الشكل المجاور مماسا لمنحنى الاقتران  $Y =\frac{1}{8} x^3$عند النقطة A ( 2,1) أقدر ميل منحنى الاقتران عند النقطة A .

الحل

$\mathit{m}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{3}}{\mathbf{2}}$

---

 

3. أقدر ميل منحنى الاقتران $y = x^3 -3x +1$ عند النقطة  ( 3, 2 ) .

الحل 

$\mathit{m}\mathbf{ }\mathbf{\approx }\mathbf{9}$

---

 

4. أقدر ميل منحنى الاقتران  $y = 4x -3x^2$عند النقطة   ( 4 - , 2 ) 

الحل

$\mathit{m}\mathbf{ }\mathbf{\approx }\mathbf{-}\mathbf{8}$

---

 

5. يمثل الاقتران $d\left(t\right) = 40t -16 t^2$المسافة التي يقطعها جسم متحرك ، حيث d  المسافة المقطوعة بالمتر ، و t  الزمن بالثواني . أقدر سرعة الجسم اللحظية بعد ثانيتين .

الحل

$\mathit{v}\mathbf{ }\mathbf{\approx }\mathbf{-}\mathbf{ }\mathbf{24}$

---

 

أرسم منحنى الاقتران f(x)  في الفترة $-2 \le x \le 2$ باستعمال جدول القيم المجاور :

 

X	-2	-1	0	1	2
F(x)	-7	-2	1	2	1

 

6. أرسم مماسا لمنحنى الاقتران عند النقطة ( 1 , 2 ) 

 

7. أقدر ميل منحنى الاقتران عند النقطة ( 1 , 2) 

$\mathit{m}\mathbf{ }\mathbf{\approx }\mathbf{-}\mathbf{2}$

 

8. ما إحداثيات النقطة التي يكون ميل المنحنى عندها صفرا؟

$( 1, 2)$

---

 

أرسم منحنى الاقتران f(x)  في الفترة $-1 \le x \le 3$ باستعمال جدول القيم المجاور :

X	-1	0	1	2	3
F(x)	4	1	0	1	4

 

9. ارسم مماسا  لمنحنى الاقتران عند النقطة ( 1 , 2)

 

10. اقدر ميل منحنى الاقتران عند النقطة ( 1 , 2)

$\mathit{m}\mathbf{ }\mathbf{\approx }\mathbf{2}$

 

11. ما إحداثيات النقطة التي يكون ميل المنحنى عندها صفرا ؟   

$(1, 0)$

---