رياضيات 7 فصل ثاني

حلول أسئلة أتحقق من فهمي 

3)

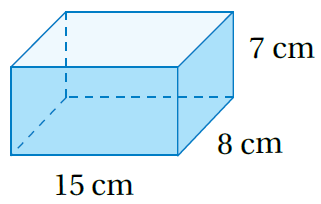
                V = Bh                        صيغة حجم المنشور 

       (l × w)h =                           تعويض الأبعاد (القاعدة مستطيلة)

   7× (8 ×15) =

             840 =                           نجد الناتج 

إذنْ، حجمُ المنشورِ يساوي 840cm³

 

4)

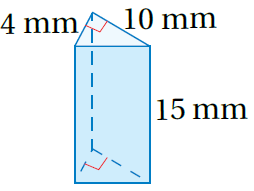
                      V = Bh                       صيغة حجم المنشور 

$$\begin{gathered} =\left(\frac{1}{2}\times 4\times 10\right)\mathrm{h} \\ =\left(\frac{1}{2}\times 4\times 10\right)\times 15 \\ =300 \end{gathered}$$                        تعويض الأبعاد(القاعدة مثلث) ، ثم أجد الناتج   

إذنْ، حجمُ المنشورِ يساوي 300mm³

 

أحواضٌ: أَجِدُ حجمَ حَوضِ الأسماكِ المجاورِ. 

 

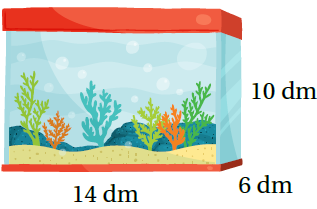
                  V = Bh                       صيغة حجم المنشور                      

        (l × w)×h =                         تعويض الأبعاد (القاعدة مستطيلة)

     (6 ×14)×10 =

                840 =                          نجد الناتج 

إذنْ، حجمُ الحوض 840dm³

---

أَجِدُ حجمَ الأُسطوانةِ المجاوِرةِ، وَأُقرّبُ إجابتي لِقربِ جزءٍ مِنْ مئةٍ.

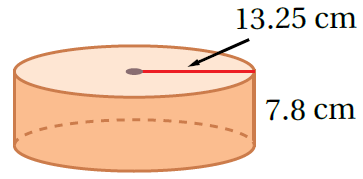
          $\mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h}$                     صيغة حجم الأسطوانة

$$\begin{gathered} =\mathrm{\pi }(13.{25}^2 )(7.8) \\ \approx 4299.88 \end{gathered}$$                 بتعويض الأبعاد ، واستخدام الآلة الحاسبة أجد الناتج 

إذنْ، حجمُ الأُسطوانةِ يساوي 4299.88cm³ تقريبًا.

 

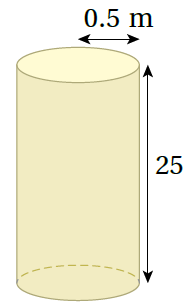
كوبٌ: كَمْ سَنتيمترًا مكعَّبًا مِنَ القهوةِ يتّسعُ لَهُ الكوبُ المجاوِرُ.

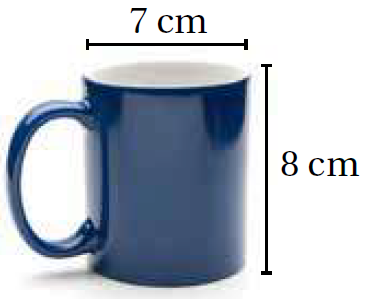
أجد حجم الكوب :

        $\mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h}$                     صيغة حجم الأسطوانة

$$\begin{gathered} =\mathrm{\pi }(3.5^2 )\left(8\right) \\ \approx 307.72 \end{gathered}$$                       بتعويض الأبعاد ، واستخدام الآلة الحاسبة أجد الناتج 

إذنْ، يتسع الكوب لـ 307.72cm³ من القهوة تقريبًا.

---

---

حلول أسئلة أتدرب وأحل المسائل 

أَجِدُ حجمَ كلِّ مجسّمٍ ممّا يأتي:

1)

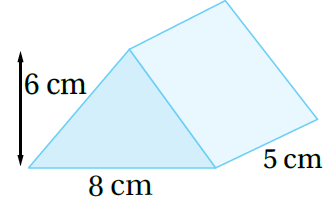
حجم منشور قاعدته على شكل مثلث 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ =\left(\frac{1}{2}\times 8\times 6\right)\times 5 \\ =120{\mathrm{cm}}^3 \end{gathered}$$                         تعويض الأبعاد(القاعدة مثلث) ، ثم أجد الناتج         

       

2)

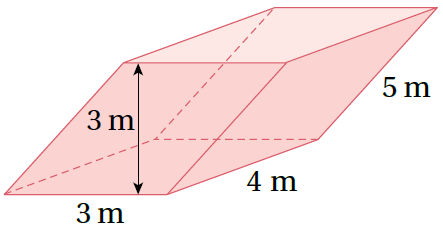
حجم منشور قاعدته على شكل مستطيل 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ =\left(3\times 4\right)\times 3 \\ =36{\mathrm{m}}^3 \end{gathered}$$                       تعويض الأبعاد(انتبه للإرتفاع الحقيقي للمنشور 3m) ، ثم أجد الناتج     

 

3)

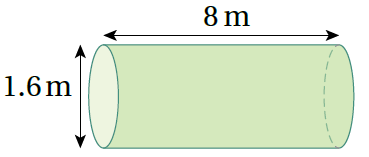
حجم أسطوانة 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(0.8^2 )\left(8\right) \\ \approx 16.08{\mathrm{m}}^3 \end{gathered}$$                       بتعويض الأبعاد ، واستخدام الآلة الحاسبة أجد الناتج 

 

4)

حجم أسطوانة 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(0.5^2 )\left(25\right) \\ \approx 19.63{\mathrm{m}}^3 \end{gathered}$$                       بتعويض الأبعاد ، واستخدام الآلة الحاسبة أجد الناتج 

 

أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي:

5) منشورٌ قاعدتُهُ مربعةٌ طولُ ضِلعِها 4m ، وَارتفاعُهُ 15m

                V = Bh                        صيغة حجم المنشور 

           (S²)h =                           تعويض الأبعاد 

      15× (4²) =

        240m² =                           نجد الناتج 

 

6) أُسطوانةٌ طولُ قطرِها 21.4dm وَارتفاعُه 33.7dm

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(10.7^2 )(33.7) \\ \approx 12115.10 {\mathrm{dm}}^3 \end{gathered}$$                تعويض الأبعاد 

 

حوضُ سباحةٍ: يبيّن الشكلُ المجاورُ حوضَ سباحةٍ على شكلِ أُسطوانةٍ، طولُ قطرِها 5.4m وَارتفاعُهُا 120cm 

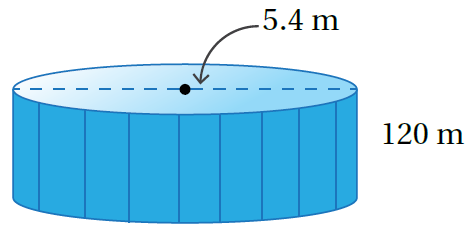
7) أَجِدُ حجمَ الحوضِ.

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(2.7^2 )(1.2) \\ \approx 27.47 {\mathrm{m}}^3 \end{gathered}$$                تعويض الأبعاد (مع الإنتباه على توحيد وحدات القياس)

8) ما كمّيةُ الماءِ بِاللّيترِ الّتي يُمكنُ أنْ يتّسعَ لَها الحوضُ؟

27470 لتر                            (1m³=1000L)

9) ما المدةُ الزمنيّةُ الّتي يحتاجُها الحوضُ حتّى يمتلئَ إذا كانَتْ سرعةُ تعبئتِهِ 50L/min

$\frac{27470}{50}=549.4 \min$

 

أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي:

10)

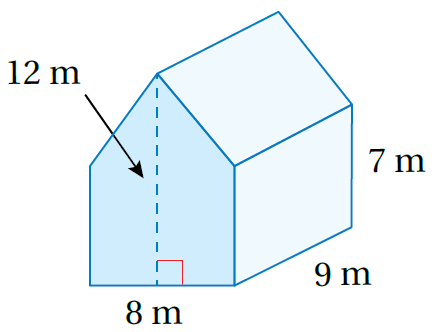
الحجم الكلي = حجم مجسم رباعي + حجم مجسم ثلاثي (قاعدته مثلث)

$$\begin{gathered} \mathrm{V}=\left(8\times 7\times 9\right)+\left(\frac{1}{2}\times 8\times \left(12-8\right)\times 9\right) \\ =684{\mathrm{cm}}^3 \end{gathered}$$

 

11)

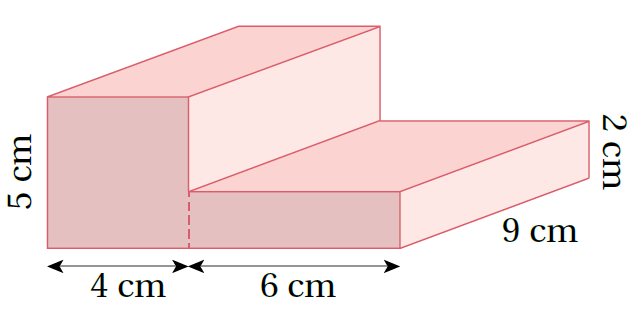
الحجم الكلي = مجموع حجم المجسمين 

$$\begin{gathered} \mathrm{ٍ}\mathrm{V}=\left(5\times 4\times 9\right)+\left(6\times 2\times 9\right) \\ =288{\mathrm{cm}}^3 \end{gathered}$$

 

أستعملُ المعلوماتِ الموضَّحةَ على كلِّ شكلٍ ممّا يأتي لإيجادِ البُعدِ المفقودِ: 

12)

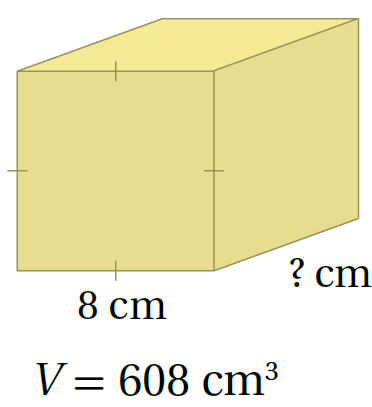
من صيغة حجم منشور قاعدته على شكل مربع نجد الإرتفاع 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ 608=8^2\times \mathrm{h} \\ \mathrm{h}=9.5 \mathrm{cm} \end{gathered}$$

 

13)

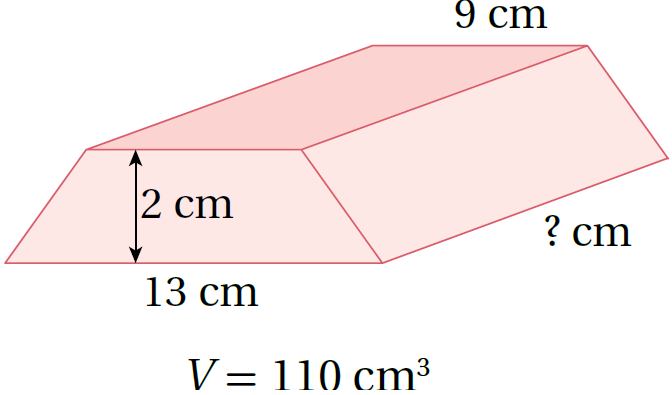
من صيغة حجم منشور قاعدته على شكل شبه منحرف 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ 110=\left(\frac{1}{2}\times 2\times \left(13+9\right)\right)\times \mathrm{h} \\ \mathrm{h}=5\mathrm{cm} \end{gathered}$$                    مساحة شبه المنحرف = مجموع القاعدتين × نصف الارتفاع 

 

14) أمطارٌ: أعودُ إلى فقرةِ (أستكشفُ) بدايةَ الدرسِ، وَأحلُّ المسألةَ.

نجد حجم الأنبوب 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(2.5^2 )\left(30\right) \\ \approx 588.75{\mathrm{cm}}^3 \end{gathered}$$

 

15) تبريرٌ: ذوَّبَ كمالٌ منشورًا رباعيًّا مِنَ الشّمْعِ أبعادُهُ 10cm,9cm,20cm لتشيكلِ شمعاتٍ على شكلِ منشورٍ قاعدتُهُ مثلَّثةٌ كَما في الشكلِ المجاورِ. كَمْ شمعةً يستطيعُ كمالٌ أنْ يصنعَ مِنْ كمّيةِ الشمعِ الّتي لَدَيْهِ؟ أبرّرُ إجابتي.

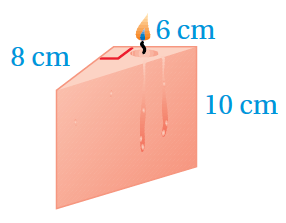
حجم المنشور الرباعي قبل الإذابة 

$$\begin{gathered} \mathrm{V}=10\times 9\times 20 \\ =1800{\mathrm{cm}}^3 \end{gathered}$$

حجم الشمعة 

$$\begin{gathered} \mathrm{V}=\left(\frac{1}{2}\times 6\times 8\right)\times 10 \\ =240{\mathrm{cm}}^3 \end{gathered}$$

عدد الشمعات = كمية الشمع مقسوما على حجم الشمعة الواحدة

$\frac{1800}{240}=7.5$

 

16) تبريرٌ: أتأملُ الشكلَ المجاورَ، ثمَّ أصفُ كيفَ يُمكنُني إيجادُ حجمِ الجسمِ المغمورِ بِالماءِ، مبررًا إجابتي، علمًا بأنَّ طولَ نصفِ قُطرِ قاعدةِ الدَّورَقِ 1.5cm ثمَّ أَجِدُ الحجمَ.

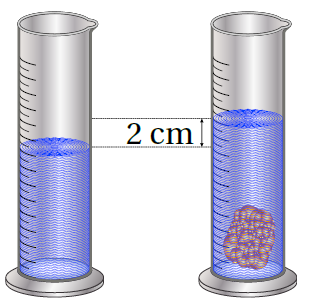
حجم المجسم المغمور = حجم الماء الزائد بعد الغمر 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(1.5^2 )\left(2\right) \\ \approx 14.3{\mathrm{cm}}^3 \end{gathered}$$                      أجد الفرق بين الحجمين 

 

17) تبريرٌ: تتكوّنُ كلُّ مجموعةٍ مِنْ أوراقِ التذكيرِ المجاورةِ مِنْ 500 ورقةٍ. هلْ يوجَدُ اختلافٌ بينَ حجمَيِ المجموعتَينِ؟ أبرّرُ إجابتي، ثمّ أَجِدُ حجمَ كلِّ مجموعةٍ، 6 cm, 6 cm, 0.02 cm علمًا أنَّ أبعادَ الورقةِ الواحدةِ

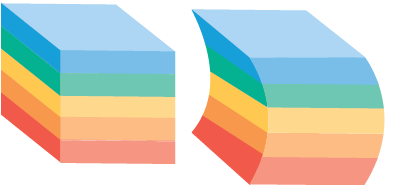
لا يوجد اختلاف بين حجمي المجموعتين لأن لهما نفس الأبعاد 

حجم المجموعة = حجم الورق × عدد أوراق المجموعة 

$$\begin{gathered} \mathrm{V}=\left(6\times 6\times 0.02\right)\times 500 \\ =360{\mathrm{cm}}^3 \end{gathered}$$

 

18)تحدٍّ: منشورٌ قاعدتُهُ على شكلِ مستطيلٍ، وَأبعادُهُ أعدادٌ كلّيةٌ، وَمساحاتُ أوجُهِهِ 30cm² , 40cm², 48cm² أَجِدُ حجمَ المنشورِ  موضِّحًا خُطواتِ الحلِّ.

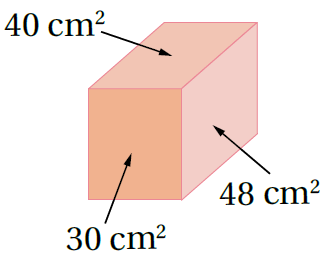
من مساحات الأوجه أجد أبعاد المنشور 

$$\begin{gathered} 40{\mathrm{cm}}^3=8\times 5 \\ 30{\mathrm{cm}}^3=5\times 6 \\ 48{\mathrm{cm}}^3=8\times 6 \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\left(5,6,8\right) \end{gathered}$$

حجم المنشور الذي قاعدته على شكل مستطيل 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ =5\times 6\times 8 \\ =240{\mathrm{cm}}^3 \end{gathered}$$

 

19) أكتبُُ كيفَ أَجِدُ حجمَ منشورٍ ثلاثيٍّ؟

نجد مساحة القاعدة ثم نضرب المساحة بارتفاع المنشور فنحصل على الحجم.

---

---

حلول أسئلة كتاب التمارين 

أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي:

1)

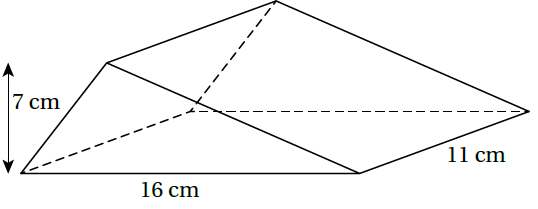
حجم منشور قاعدته على شكل مثلث 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ =\left(\frac{1}{2}\times 7\times 16\right)\times 11 \\ =616{\mathrm{cm}}^3 \end{gathered}$$

2)

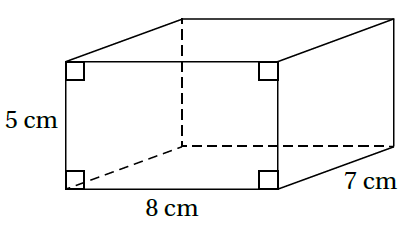
حجم منشور قاعدته على شكل مستطيل 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ =5\times 8\times 7 \\ =280{\mathrm{cm}}^3 \end{gathered}$$

3)

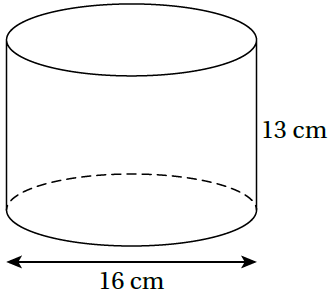
حجم الاسطوانة 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(8^2 )\left(13\right) \\ \approx 2613.8{\mathrm{cm}}^3 \end{gathered}$$

 

أستعملُ المعلوماتِ الموضَّحةَ على كلِّ شكلٍ ممّا يأتي لَِجِدَ البُعدَ المفقودَ:

4)

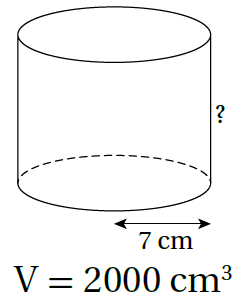
من حجم الأسطوانة أجد الارتفاع 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ 2000=\mathrm{\pi }(7^2 )\mathrm{h} \\ \approx 13\mathrm{cm} \end{gathered}$$

 

5)

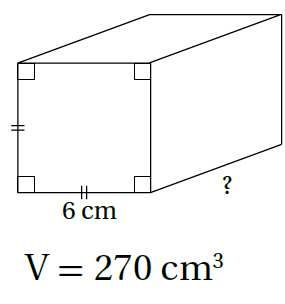
من حجم المنشور الذي قاعدته مربع أجد الإرتفاع 

$$\begin{gathered} \mathrm{V}={\mathrm{s}}^2\times \mathrm{h} \\ 270=6^2\times \mathrm{h} \\ \mathrm{h}=7.5\mathrm{cm} \end{gathered}$$

 

6)

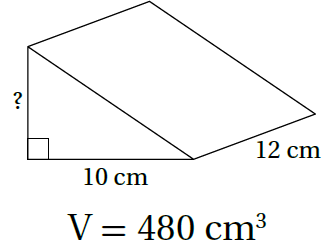
من حجم المنشور الذي قاعدته مثلث أجد ارتفاع المثلث 

$$\begin{gathered} 480=\left(\frac{1}{2}\times 10\times \mathrm{x}\right)\times 12 \\ \mathrm{x}=8\mathrm{cm} \end{gathered}$$

7) حافظةٌ: يبيّنُ الشكلُ المجاورُ حافظةً للماءِ الساخنِ، أَجِدُ كمّيّةَ الماءِ الّتي تتّسعُ لَها الحافظةُ.

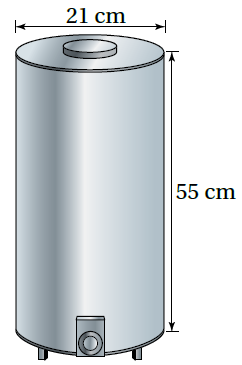
أجد حجم الأسطوانة 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(10.5^2 )\times 55 \\ \approx 19049.83{\mathrm{cm}}^3 \end{gathered}$$

 

أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي:

8) أُسطُوانةٌ طولُ قطرِها 24m وَارتفاعُها 28m 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }({12}^2 )\times 28 \\ \approx 12666.9{\mathrm{m}}^3 \end{gathered}$$

 

9) منشورٌ رباعيٌّ قاعدتُهُ مستطيلةُ الشكلِ، طولُهُا 25m وَعَرضُهُا 6m وَارتفاعُهُ 9m 

$$\begin{gathered} \mathrm{V}=25\times 6\times 9 \\ =1350{\mathrm{m}}^3 \end{gathered}$$

 

ملحٌ: يبيّنُ الشكلُ المجاورُ عُلبتَينِ لِحفظِ الملحِ:

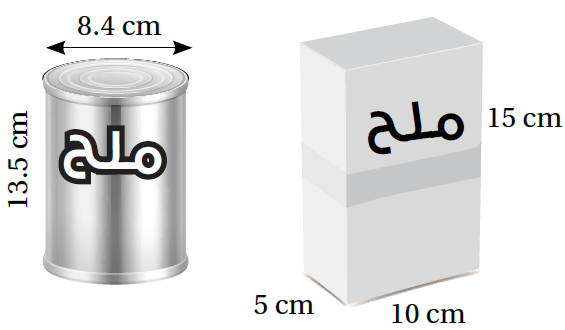
10) أقارنُ بينَ حجمَيِ العلبتَينِ.

حجم العلبة التي على شكل منشور رباعي 

$$\begin{gathered} \mathrm{V}=\mathrm{Bh} \\ =5\times 10\times 15 \\ =750{\mathrm{cm}}^3 \end{gathered}$$

حجم العلبة التي على شكل الأسطوانة 

$$\begin{gathered} \mathrm{V}={\mathrm{\pi r}}^2 \mathrm{h} \\ =\mathrm{\pi }(4.2^2 )\times 13.5 \\ \approx 748.13{\mathrm{cm}}^3 \end{gathered}$$

العلبة على شكل منشور رباعي أكبر من العلبة الأسطوانية 

11) أيُّ العُلبتَينِ أفضلُ مِنْ حيثُ التخزينُ وَالنقلُ وَالتوزيعُ؟ أبرّرُ إجابتي.

العلبة على شكل منشور رباعي لأنها الأكبر حجما لذلك فهي الأفضل من حيث التخزين والنقل والتوزيع 

 

12) تبريرٌ: حوضُ سمكٍ على شكلِ منشورٍ رباعيٍّ أبعادُهُ 45cm,30cm,25cm  تقولُ ريماسُ: (إذا أصبحَتْ أبعادُ حوضِ السمكِ مثلَيِ الأبعادِ الأصليةِ، فَإنَّنا نحتاجُ إلى مثلَيْ كمّيّةِ الماءِ لِملْءِ الحوضِ الجديدِ) هلْ ما تقولُهُ ريماسُ صحيحٌ؟ أبرّرُ إجابتي. 

حجم المنشور الأصلي 

$$\begin{gathered} {\mathrm{V}}_1=\mathrm{Bh} \\ =45\times 30\times 25 \\ =33750 {\mathrm{cm}}^3 \end{gathered}$$

حجم المنشور بعد الزيادة 

$$\begin{gathered} {\mathrm{V}}_2=\mathrm{Bh} \\ =90\times 60\times 50 \\ =270000 {\mathrm{cm}}^3 \\ {\mathrm{V}}_2\ne 2{\mathrm{V}}_1 \end{gathered}$$