فكرةُ الدّرس: أجدُ حجم المنشور الرُّباعيّ، وأجدُ مساحتةُ السّطحيّة.
مفهومٌ أساسيٌّ: حجمُ المنشور الرُّباعيّ
|
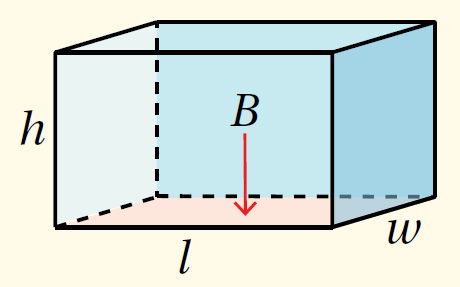
بالكلمات: حجمُ المنشور الرُّباعيّ (V) يُساوي ناتج ضرب مساحة القاعدة (B) في الارتفاع (h)، ويُساوي ناتج ضرب طوله (l) في عرضه (w) في ارتفاعه (h). بالرُّموز : V = B × h V = l × w × h |
 |
مثال
أجدُ حجم كُلّ منشور رُباعيّ ممّا يأتي:
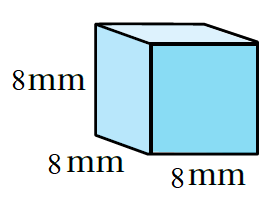 |
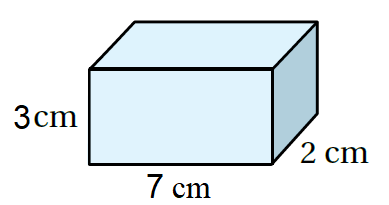 |
| صيغةُ حجم المنشور الرُّباعيّ | صيغةُ حجم المنشور الرُّباعيّ |
يُمكنُ استعمالُ صيغة حجم المنشور لكتابة مُعادلة ثُمّ حلّها لإيجاد بُعد مجهول من أبعاد المنشور الرُّباعيّ.
مثال
أجدُ قيمة x في كُلّ المنشور الرُباعيّ التالي علمًا أنّ حجمه 189cm3
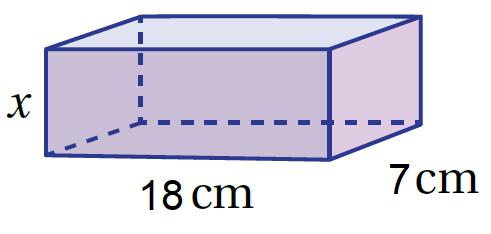 |
| صيغةُ حجم المنشور الرُّباعيّ |
تعلّمتُ سابقًا أنّ المساحة الكُلّيّة (S.A) (total surface area ) لسطح أيّ مُجسّم تُساوي مجموع مساحات أوجُهه جميعها؛ لذا يُمكنُ إيجادُ المساحة الكُلّيّة لسطح المنشور الرُّباعيّ بجمع مساحات الأوجُه المُستطيلة السّتّة. أمّا المساحةُ الجانبيّةُ (L.A) (lateral area ) لسطح المنشور فهي مجموعُ مساحات أوجُهه الجانبيّة الأربعة.
|
مفهومٌ أساسيٌّ: المساحةُ الجانبيّةُ والمساحةُ الكُلّيّةُ لسطح المنشور |
|
|
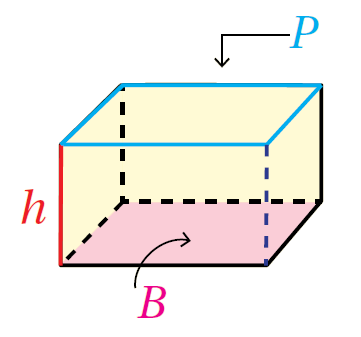
المساحةُ الجانبيّةُ بالكلمات: المساحةُ الجانبيّةُ L.A لسطح المنشور الرُّباعيّ تُساوي مجموع مساحات أوجُهه الجانبيّة الأربعة، وهي ناتجُ ضرب ارتفاع المنشور (h) في مُحيط قاعدته (p) بِالرُّموزِ: L.A = P h |
 |
|
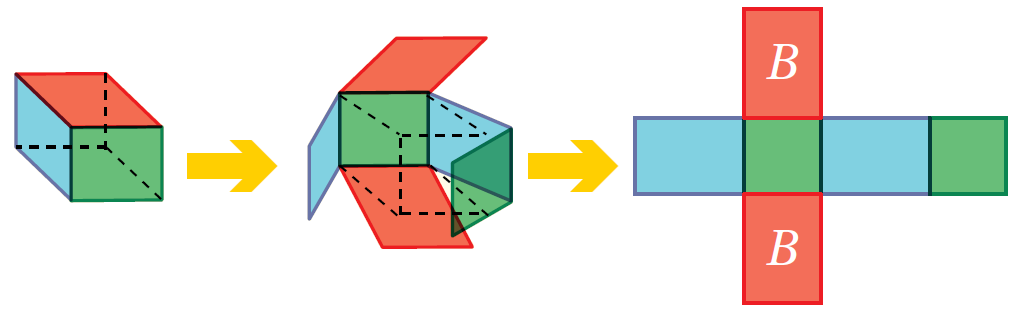
المساحةُ الكُلّيّةُ بالكلمات: المساحةُ الكُلّيّةُ S.A لسطح المنشور الرُّباعيّ تُساوي مجموع مساحات أوجُهه المُستطيلة السّتّة، أو مجموع مساحته الجانبيّة ومساحتي قاعدتيه. بِالرُّموزِ: S.A = L.A + 2B |
 |
|
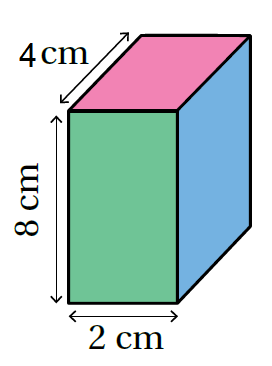
مثال أجدُ المساحة الجانبيّة والمساحة الكُلّيّة لسطح المنشور الرُباعيّ التالي: |
 |
|||||
| الجواب | ||||||
|
||||||
|
||||||
|
||||||
|
يُمكنُ استعمالُ صيغتي حجم المنشور الرُّباعيّ ومساحة سطحه الكُلّيّة في كثير من مواقف الحياة.
|
مثال يظهرُ في الصّورة المُجاورة صُندوقُ جهاز حاسوب على شكل منشور رُباعيّ حجمُهُ وطولُهُ وعرضُهُ 1) أجدُ ارتفاع الصُّندوق (h). 2) أجدُ المساحة الكُلّيّة لسطح الصُّندوق. الجواب 1) |
|
|||
|
2) أجدُ مُحيط قاعدة الصُّندوق أجدُ المساحة الجانبيّة لسطح الصُّندوق أجدُ مساحة قاعدة الصُّندوق أجدُ المساحة الكُلّيّة لسطح الصُّندوق |
