رياضيات فصل أول

مفهوم أساسي:

الزاويةُ الداخليةُ لمضلّعٍ (Interior angle) هيَ الزاويةُ الناتجةُ منَ التقاءِ ضِلْعينِ متجاورينِ في المضلّعٍ وتقعُ داخلَهُ، ومجموعُ قياساتِ الزوايا الداخليةِ (S) لمضلع هو S = (n −2)×180° ، حيث n  تمثِّلُ عددَ الأضلاعِ. 

مثال1: أجدُ مجموعَ قياساتِ الزوايا الداخليةِ لكلِّ مُضلَّعٍ ممّا يأتي: 

1) السُّباعيُّ:

صيغةُ مجموعِ قياساتِ زوايا المضلّعِ الداخليةِ               $\mathrm{S}=(\mathrm{n}-2)\times 180°$

                    $\mathrm{S}=(7-2)\times 180°$                                                                   n = أعوِّضُ 7

أُبسِّطُ                                                                         $\mathrm{S}=5\times 180°=900°$                 

2) العُشاريُّ:

صيغةُ مجموعِ قياساتِ زوايا المضلّعِ الداخليةِ                         $\mathrm{S}=(\mathrm{n}-2)\times 180°$                     

                    $\mathrm{S}=(10-2)\times 180°$                                                                           n = أعوِّضُ 10

أُبسِّطُ                                                                                   $\mathrm{S}=8\times 180°=1440°$   

 

مفهوم أساسي:

المضلّعُ المُنتَظَمُ (Regular polygon) : هوَ مُضلَّعٌ جميعُ أضلاعِهِ لها الطولُ نفسُهُ، وزواياهُ الداخليةُ جميعُها لها القياسُ نفسُهُ.

قياسُ الزاويةِ الداخليةِ (x) لمضلَّعٍ مُنْتَظَمٍ عددُ أضلاعِهِ n يُساوي مجموعَ قياساتِ زواياهُ الداخليةِ (s) مقسومًا على عددِ أضلاعِهِ.

$\mathbf{x}\mathbf{°}\mathbf{=}\frac{\mathbf{(}\mathbf{n}\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{\times }\mathbf{180}\mathbf{°}}{\mathbf{n}}$

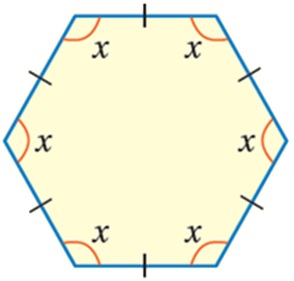
مثال2: منَ الحياةِ صمّمَتْ ماجدةُ إطاراتٍ خشبيّةً على شكلِ مضلعاتٍ سُداسيّةٍ منتظمةٍ. أجِدُ قياسَ الزاويةِ الداخليةِ لتلكَ الإطاراتِ.

صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ              $\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                 

أعوض n=6                                                                        $$\begin{gathered} \mathrm{x}°=\frac{(6-2)\times 180°}{6} \\ =120° \end{gathered}$$                 

 

مفهوم أساسي:

الزاويةُ الخارجيّةُ للمضلّعِ (Exterior angle): هيَ الزاويةُ المتشكِّلةُ منْ أحدِ الأضلاعِ وامتدادِ الضلعِ المجاورِ لهُ. ومجموعُ قياساتِ الزوايا الخارجيّةِ لأيِّ مضلّعٍ منتظمٍ عددُ أضلاعِهِ (n) - زاويةٌ واحدةٌ لكلِّ رأسٍ -

هوَ °360 ، وفي هذهِ الحالةِ يكونُ قياسُ كلِّ زاويةٍ خارجيّةٍ (x) منْ هذهِ الزوايا:

$\mathbf{x}\mathbf{°}\mathbf{=}\frac{\mathbf{360}\mathbf{°}}{\mathbf{n}}$

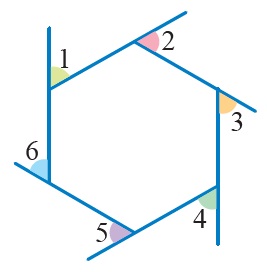
مثال3: أجدُ قياسَ الزاويةِ الخارجيةِ للسُّباعيِّ المنتظَمِ، لأقربِ درجةٍ:

 

أكتبُ المعادلةَ                         $\mathrm{x}°=\frac{360°}{\mathrm{n}}$                               

أعوض n=7                               $$\begin{gathered} \mathrm{x}°=\frac{360°}{7} \\ \approx 51° \end{gathered}$$                             

 

يمكنُني استخدامُ مجموعِ قياساتِ زوايا مُضلَّعٍ لإيجادِ قياساتِ زوايا مجهولةٍ فيهِ.

مثال4: أجدُ قياساتِ الزوايا المجهولةِ في الشكلِ المجاورِ:

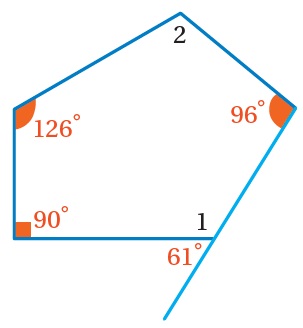
1) $\mathbf{m}\mathbf{\angle }\mathbf{1}$

زاويتانِ متجاورتانِ على مستقيمٍ                 $$\begin{gathered} \mathrm{m}\angle 1+ 61°=180° \\ \mathrm{m}\angle 1=119° \end{gathered}$$                 

2) $\mathbf{m}\mathbf{\angle }\mathbf{2}$

أولًا: أجدُ مجموعَ قياساتِ زوايا المضلَّع المُعْطى.

صيغةُ مجموعِ قياساتِ زوايا المضلّعِ                       $\mathrm{S}=(\mathrm{n}-2)\times 180°$                      

أعوض n=5                                                              $$\begin{gathered} \mathrm{S}=(5-2)\times 180° \\ \mathrm{S}=3\times 180°=540° \end{gathered}$$                 

ثانيًا: أستعملُ مجموعَ قياساتِ الزوايا لإيجادِ قياسِ الزاويةِ المجهولةِ.

أجمعُ قياساتِ الزوايا الداخليةِ، وَأساويها بِ ° 540           $\mathrm{m}\angle 2+119°+96°+126°+90°=540°$                   

أجد الناتج                                                                             $$\begin{gathered} \mathrm{m}\angle 2+431°=540° \\ \mathrm{m}\angle 2=109° \end{gathered}$$                                                    

 

أستخدمُ المعادلاتِ الخطِّيَّةَ لإيجادِ عددِ أضلاعِ مضلَّعٍ منتظَمٍ أعلَمُ قياسَ زاويتِهِ الداخليّةِ. 

مثال5: أجدُ عددَ أضلاعِ مضلَّعٍ منتظَمٍ قياسُ زاويتِهِ الداخليّةِ °135

بِما أنَّ المضلَّعَ منتظَمٌ، فإنَّ زواياهُ جميعَها لها القياسُ نفسُهُ        $\text{S=n×135°}$                                                               

صيغةُ مجموعِ قياساتِ زوايا المضلَّعِ                                     $\mathrm{S}=(\mathrm{n}-2)\times 180°$                                                      

أكتبُ معادلةً                                                                             $\mathrm{n}\times 135°=(\mathrm{n}-2)\times 180°$                                           

خاصيةُ التوزيعِ                                                                           $135°\mathrm{n}=180°\mathrm{n}-360°$                                              

أجد الناتج                                                                                              $$\begin{gathered} - 45°\mathrm{n}=-360° \\ \mathrm{n}=8 \end{gathered}$$                                                     

إذنْ، عددُ أضلاعِ المضلَّعِ ثمانيةٌ.