رياضيات فصل أول

حلول أسئلة أتحقق من فهمي

3) التساعي

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                             صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(9-2)\times 180° \\ \mathrm{S}=7\times 180° \\ =1260° \end{gathered}$$                             بتعويض n=9

4) ذو أربعة عشر ضلعاً

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                             صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(14-2)\times 180° \\ \mathrm{S}=12\times 180° \\ =2160° \end{gathered}$$                           بتعويض n=14

5) ذو ثمانية عشر ضلعاً

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                             صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(18-2)\times 180° \\ \mathrm{S}=16\times 180° \\ =2880° \end{gathered}$$                           بتعويض n=18

 

أجدُ قياسَ الزاويةِ الداخليةِ لكلِّ مُضلَّعٍ منتظمٍ ممّا يأتي:

2)الثماني المنتظَمُ.

$\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                           صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{(8-2)\times 180°}{8} \\ \mathrm{x}°=135° \end{gathered}$$                           بتعويض n=8

3) العُشاريُّ المنتظَمُ.

$\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                           صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{(10-2)\times 180°}{10} \\ \mathrm{x}°=144° \end{gathered}$$                         بتعويض n=10

 

2)السُداسِيُّ المنتظَمُ.

$\mathrm{x}°=\frac{360°}{\mathrm{n}}$                                        أكتبُ المعادلةَ

$$\begin{gathered} \mathrm{x}°=\frac{360°}{6} \\ = 60° \end{gathered}$$                                        بتعويض n=6   

3) العُشاريُّ المنتظَمُ.

$\mathrm{x}°=\frac{360°}{\mathrm{n}}$                                        أكتبُ المعادلةَ

$$\begin{gathered} \mathrm{x}°=\frac{360°}{10} \\ =36° \end{gathered}$$                                        بتعويض n=10   

4) ذو خمسةَ عشرَ ضلعًا منتظمًا.

$\mathrm{x}°=\frac{360°}{\mathrm{n}}$                                        أكتبُ المعادلةَ

$$\begin{gathered} \mathrm{x}°=\frac{360°}{15} \\ =24° \end{gathered}$$                                        بتعويض n=15   

 

أجد قياسات الزوايا المجهولة في الشكل المجاور

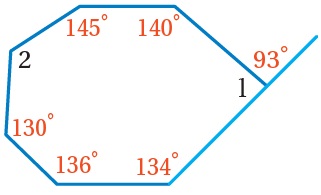
3) m∠1

$$\begin{gathered} \mathrm{m}\angle 1+93°=180° \\ \mathrm{m}\angle 1=87° \end{gathered}$$                           زاويتانِ متجاورتانِ على مستقيمٍ

4) m∠2

أولًا: أجدُ مجموعَ قياساتِ زوايا المضلَّع المُعْطى.

$$\begin{gathered} \mathrm{S}=(\mathrm{n}-2)\times 180° \\ \mathrm{S}=(7-2)\times 180° \\ \mathrm{S}=5\times 180°=900° \end{gathered}$$                         بتعويض n=7 في صيغةُ مجموعِ قياساتِ زوايا المضلّعِ    

ثانيًا: أستعملُ مجموعَ قياساتِ الزوايا لإيجادِ قياسِ الزاويةِ المجهولةِ.

$$\begin{gathered} \mathrm{m}\angle 2+145°+140°+87°+134°+136°+130°=900° \\ \mathrm{m}\angle 2+772° \\ \mathrm{m}\angle 2=128° \end{gathered}$$                           أجمعُ قياساتِ الزوايا الداخليةِ، وَأساويها بِ ° 540

 

. أجدُ عددَ أضلاعِ مضلَّعٍ منتظَمٍ قياسُ زاويتِهِ الداخليةِ ° 140

$\text{S=n×140°}$                                       بِما أنَّ المضلَّعَ منتظَمٌ، فإنَّ زواياهُ جميعَها لها القياسُ نفسُهُ

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                              صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{n}\times 140°=(\mathrm{n}-2)\times 180° \\ 140°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 40°\mathrm{n} \\ \mathrm{n} = 9 \end{gathered}$$                   نجد الناتج

إذنْ، عددُ أضلاعِ المضلَّعِ تسعة.

---

---

حلول أسئلة أتدرب وأحل المسائل 

أجدُ مجموعَ قياساتِ الزوايا الداخليّةِ للمضلَّعِ المُعطى عددُ أضلاعِهِ في كلٍّ ممّا يأتي:

1) 11 ضلعًا.

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                            صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(11-2)\times 180° \\ \mathrm{S}=9\times 180° \\ =1620° \end{gathered}$$                          بتعويض n=11

2) 13 ضلعًا.

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                            صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(13-2)\times 180° \\ \mathrm{S}=11\times 180° \\ =1980° \end{gathered}$$                          بتعويض n=13

3) 20 ضلعًا.

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                            صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(20-2)\times 180° \\ \mathrm{S}=18\times 180° \\ =3240° \end{gathered}$$                          بتعويض n=20

4) 32 ضلعًا.

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                            صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{S}=(32-2)\times 180° \\ \mathrm{S}=30\times 180° \\ =5400° \end{gathered}$$                          بتعويض n=32

أجدُ قياسَ الزاويةِ الداخليةِ للمضلَّعِ المنتظمِ المُعْطى عَددُ أضلاعِه في كلٍّ ممّا يأتي (أُقرِّبُ إجابتي إلى أَقْرَبِ درجةٍ)

5) 9 أضلاعٍ.

$\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{(9-2)\times 180°}{9} \\ \mathrm{x}°=140° \end{gathered}$$                         بتعويض n=9

6) 11 ضلعًا.

$\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{(11-2)\times 180°}{11} \\ \mathrm{x}°\approx 147° \end{gathered}$$                       بتعويض n=11

7) 12 ضلعًا.

$\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{(12-2)\times 180°}{12} \\ \mathrm{x}°=150° \end{gathered}$$                       بتعويض n=12

8) 20 ضلعًا.

$\mathrm{x}°=\frac{(\mathrm{n}-2)\times 180°}{\mathrm{n}}$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{(20-2)\times 180°}{20} \\ \mathrm{x}°=162° \end{gathered}$$                       بتعويض n=20

أجدُ قياسَ الزاويةِ الخارجيةِ لكلٍّ منَ المضلّعاتِ المنتظمةِ الآتيةِ (أُقرِّبُ إجابتي إلى أَقْرَبِ درجةٍ):

9) خماسيٌّ.

$$\begin{gathered} \mathrm{x}°=\frac{360°}{\mathrm{n}} \\ =\frac{360°}{5} \\ =72° \end{gathered}$$                                      بتعويض n=5 في صيغة قياس الزاوية الخارجية للمضلع المنتظم                   

10) ثمانيٌّ.

$$\begin{gathered} \mathrm{x}°=\frac{360°}{\mathrm{n}} \\ =\frac{360°}{8} \\ =45° \end{gathered}$$                                      بتعويض n=8 في صيغة قياس الزاوية الخارجية للمضلع المنتظم 

11) تساعيٌّ.

$$\begin{gathered} \mathrm{x}°=\frac{360°}{\mathrm{n}} \\ =\frac{360°}{9} \\ =40° \end{gathered}$$                                      بتعويض n=9  في صيغة قياس الزاوية الخارجية للمضلع المنتظم 

12) ذو عشرينَ ضلعًا.

$$\begin{gathered} \mathrm{x}°=\frac{360°}{\mathrm{n}} \\ =\frac{360°}{20} \\ =18° \end{gathered}$$                                      بتعويض n=20 في صيغة قياس الزاوية الخارجية للمضلع المنتظم  

أجدُ قياسَ الزاويةِ المجهولةِ في كلِّ شكلٍ ممّا يأتي:

13)

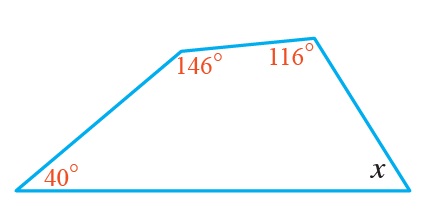
شكل رباعي غير منتظم 

$$\begin{gathered} \mathrm{S}=(4-2)\times 180° \\ \mathrm{S}=2\times 180° \\ =360° \end{gathered}$$                           صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

نجد قياس الزاوية المجهولة 

$$\begin{gathered} \mathrm{m}\angle \mathrm{x}=360°-\left(146+116+40\right)° \\ \mathrm{m}\angle \mathrm{x}=58° \end{gathered}$$

14)

نجد قياس الزاوية المجهولة y

$$\begin{gathered} \mathrm{m}\angle \mathrm{y}=180°-67° \\ =113° \end{gathered}$$                         زاويتانِ متجاورتانِ على مستقيمٍ

شكل خماسي غير منتظم 

$$\begin{gathered} \mathrm{S}=(5-2)\times 180° \\ \mathrm{S}=3\times 180° \\ =540° \end{gathered}$$                           صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

نجد قياس الزاوية المجهولة x

$$\begin{gathered} \mathrm{m}\angle \mathrm{x}=540°-\left(100+116+120+113\right)° \\ \mathrm{m}\angle \mathrm{x}=91° \end{gathered}$$

أجدُ عددَ أضلاعِ المضلَّعِ المنتظَمِ المُعْطى قياسُ زاويتِهِ الداخليةِ في كلٍّ ممّا يأتي:

15) $\mathbf{162}\mathbf{°}$

$\text{S=n×162°}$                                       بِما أنَّ المضلَّعَ منتظَمٌ، فإنَّ زواياهُ جميعَها لها القياسُ نفسُهُ

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                              صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{n}\times 162°=(\mathrm{n}-2)\times 180° \\ 162°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 18°\mathrm{n} \\ \mathrm{n} = 20 \end{gathered}$$                  أجد الناتج 

16) $\mathbf{144}\mathbf{°}$

$\text{S=n×144°}$                                       بِما أنَّ المضلَّعَ منتظَمٌ، فإنَّ زواياهُ جميعَها لها القياسُ نفسُهُ

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                              صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{n}\times 144°=(\mathrm{n}-2)\times 180° \\ 144°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 36°\mathrm{n} \\ \mathrm{n} = 10 \end{gathered}$$                  أجد الناتج

17) $\mathbf{150}\mathbf{°}$

$\text{S=n×150°}$                                       بِما أنَّ المضلَّعَ منتظَمٌ، فإنَّ زواياهُ جميعَها لها القياسُ نفسُهُ

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                              صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{n}\times 150°=(\mathrm{n}-2)\times 180° \\ 150°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 30°\mathrm{n} \\ \mathrm{n} = 12 \end{gathered}$$                  أجد الناتج

 

18) جَبْرٌ: أكتبُ معادلةً، ثمَّ أحلُّها بإيجادِ قياسِ زوايا المضلَّعِ المجاورِ.

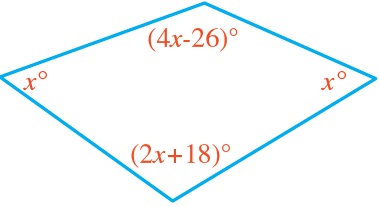
مجموع قياسات الزوايا الداخلية للشكل الرباعي :

 $$\begin{gathered} \mathrm{x}°+\mathrm{x}°+(4\mathrm{x}-26)°+(2\mathrm{x}+18)°=360° \\ 8\mathrm{x}°-8°=360° \\ \mathrm{x}°=46° \end{gathered}$$

قياس الزوايا : 

$46°,46°,110°,158°$

 

19) يريدُ محمدٌ صُنْعَ إطارٍ على شكلِ مضلَّعٍ تُساعيٍّ منتظَمٍ باستعمالِ ألواحٍ خشبيةٍ. ما الزاويةُ التي سيقطعُ بها كلَّ لوحٍ عندَ طرفَيْهِ؛ ليتمكَّنَ منْ جَمْعِ الألواحِ بعضِها معَ بعضٍ لتشكيلِ الإطارِ المطلوب؟ أبرِّرُ إجابتي.

نجد قياس الزاوية ، وهي زاوية داخلية 

$$\begin{gathered} \mathrm{x}°=\frac{(9-2)\times 180°}{9} \\ =140° \end{gathered}$$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

وعليه ليتمكن من جمع اللوحين لتشكيل الإطار المطلوب ستكون زاوية كل من الطرفين °70

 

20) عُملاتٌ: تمثِّلُ القطعةُ النقديّةُ منْ فئةِ رُبْعِ الدينارِ مُضلَّعًا منتظَمًا. أجدُ قياسَ كلٍّ منْ زاويتِهِ الداخليةِ وزاويتِهِ الخارجيةِ.

عدد الأضلاع 7:

$$\begin{gathered} \mathrm{x}°=\frac{(7-2)\times 180°}{7} \\ =129° \end{gathered}$$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

$$\begin{gathered} \mathrm{x}°=\frac{360°}{\mathrm{n}} \\ =\frac{360°}{7} \\ \approx 51° \end{gathered}$$                                      بتعويض n=7 في صيغة قياس الزاوية الخارجية للمضلع المنتظم  

 

قياسُ الزاويةِ الداخليةِ لمضلعٍ منتظمٍ يساوي 4x وقياسُ زاويتِهِ الخارجيةِ يساوي 2x : 

21) أجدُ قيمةَ x

$$\begin{gathered} 2\mathrm{x}+4\mathrm{x}=180° \\ 6\mathrm{x}=180° \\ \mathrm{x}=30° \end{gathered}$$                                مجموع قياس الزاوية الداخلية والخارجية 180° ، تمثل خط مستقيم 

 

22) أجدُ قياسَ الزاويةِ الداخليةِ وقياسَ الزاويةِ الخارجيةِ.

$2\mathrm{x}=60°$                                 قياس الزاوية الخارجية 

$4\mathrm{x}=120°$                                 قياس الزاوية الداخلية 

23) أجدُ عددَ أضلاعِ المضلعِ المنتظمِ. 

نستخدم الزاوية الداخلية لإيجاد عدد الأضلاع 

$\text{S=n×120°}$                                     الزاوية الداخلية للضلع المنتظم 

$\mathrm{S}=(\mathrm{n}-2)\times 180°$                           صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

$$\begin{gathered} \mathrm{n}\times 120°=(\mathrm{n}-2)\times 180° \\ 120°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 60°\mathrm{n} \\ \mathrm{n} = 6 \end{gathered}$$               أجد الناتج 

 

24) تبريرٌ: هلْ يوجدُ مضلّعٌ منتظَمٌ قياسُ زاويتِهِ الداخليةِ ° 160 ؟ أبرِّرُ إجابتي.

نعوض في معادلة الزوايا الداخلية لإيجاد عدد الأضلاع  

$$\begin{gathered} \mathrm{n}\times 160°=(\mathrm{n}-2)\times 180° \\ 160°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 20°\mathrm{n} \\ \mathrm{n} = 18 \end{gathered}$$            بمساواة الزاوية الداخلية مع صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

 

25) تحدٍّ: إذا كانَ المضلّعانِ في الشكلِ المجاورِ منتظَمينِ، فأجدُ $\mathbf{m}\mathbf{\angle }\mathbf{RND}$ ، مُبرِّرًا إجابتي. 

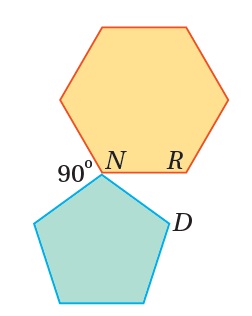
مجموع قياس الزوايا الداخلية للشكلين والزاويتان الخارجيتان = 360°

$\mathrm{m}\angle {\mathrm{x}°}_5+\mathrm{m}\angle {\mathrm{x}°}_6+90°+\mathrm{m}\angle \mathrm{RND}=360°$

$$\begin{gathered} \mathrm{x}°=\frac{(6-2)\times 180°}{6} \\ =120° \end{gathered}$$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ السداسي المنتظَمِ 

$$\begin{gathered} \mathrm{x}°=\frac{(5-2)\times 180°}{5} \\ =108° \end{gathered}$$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ الخماسي المنتظَمِ

$\mathrm{m}\angle \mathrm{RND}=42°$                               بالتعويض في مجموع قياسات الزوايا 

 

26) أكتبُ فقرةً قصيرةً أبيِّنُ فيها العلاقةَ بينَ عددِ أضاعِ المضلّعِ المنتظَمِ وقياسِ زاويتِهِ الداخليةِ. 

قياس الزاوية الداخلية لمضلع منتظم يساوي مجموع قياسات زواياه الداخلية مقسوماً على عدد أضلاعه

---

---

حلول أسئلة كتاب التمارين 

أجدُ مَجموعَ قِياساتِ الزّوايا الدّاخليّةِ لكلِّ مُضَلّعٍ مِمّا يَأْتي 

1) ذو 19 ضلعًا.

$$\begin{gathered} \mathrm{S}=(19-2)\times 180° \\ \mathrm{S}=17\times 180° \\ =3060° \end{gathered}$$                       بتعويض n=19 في صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

2) ذو 21 ضلعًا.

$$\begin{gathered} \mathrm{S}=(21-2)\times 180° \\ \mathrm{S}=19\times 180° \\ =3420° \end{gathered}$$                       بتعويض n=21 في صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

3) ذو 30 ضلعًا.

$$\begin{gathered} \mathrm{S}=(30-2)\times 180° \\ \mathrm{S}=28\times 180° \\ =5040° \end{gathered}$$                       بتعويض n=30 في صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

4) ذو 33 ضلعًا.

$$\begin{gathered} \mathrm{S}=(33-2)\times 180° \\ \mathrm{S}=31\times 180° \\ =5580° \end{gathered}$$                       بتعويض n=33 في صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

 

أجِدُ عَددَ أضْلاعِ مُضَلّعٍ مُنتَظَمٍ، قِياسُ زاويتِهِ الدّاخِليَّةِ:

5) $\mathbf{156}\mathbf{°}$

$$\begin{gathered} \mathrm{n}\times 156°=(\mathrm{n}-2)\times 180° \\ 156°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 24°\mathrm{n} \\ \mathrm{n} = 15 \end{gathered}$$            بمساواة الزاوية الداخلية مع صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

6) $\mathbf{160}\mathbf{°}$

$$\begin{gathered} \mathrm{n}\times 160°=(\mathrm{n}-2)\times 180° \\ 160°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 20°\mathrm{n} \\ \mathrm{n} = 18 \end{gathered}$$            بمساواة الزاوية الداخلية مع صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

7) $\mathbf{165}\mathbf{°}$

$$\begin{gathered} \mathrm{n}\times 165°=(\mathrm{n}-2)\times 180° \\ 165°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 15°\mathrm{n} \\ \mathrm{n} = 24 \end{gathered}$$            بمساواة الزاوية الداخلية مع صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

8) $\mathbf{170}\mathbf{°}$

$$\begin{gathered} \mathrm{n}\times 170°=(\mathrm{n}-2)\times 180° \\ 170°\mathrm{n}=180°\mathrm{n}-360° \\ 360° = 10°\mathrm{n} \\ \mathrm{n} = 36 \end{gathered}$$            بمساواة الزاوية الداخلية مع صيغةُ مجموعِ قياساتِ زوايا المضلّعِ

 

أجدُ قياسَ الزّاوِيةِ الدّاخليَّةِ والخارجيّةِ لكُلٍّ منَ المُضَلّعاتِ المُنتَظمَةِ الآتيةِ:

9)  ذو 24 ضلعًا.

قياس الزاوية الداخلية:

$$\begin{gathered} \mathrm{x}°=\frac{(24-2)\times 180°}{24} \\ =165° \end{gathered}$$                     بتعويض n=24 صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

قياس الزاوية الخارجية:

$$\begin{gathered} \mathrm{x}°=\frac{360°}{24} \\ =15° \end{gathered}$$                                    بتعويض n=24 في صيغةُ قياسِ الزاويةِ الخارجية للمضلَّعِ المنتظَمِ

10) ذو 40 ضلعًا.

قياس الزاوية الداخلية:

$$\begin{gathered} \mathrm{x}°=\frac{(40-2)\times 180°}{40} \\ =171° \end{gathered}$$                     بتعويض n=40 في صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

قياس الزاوية الخارجية:

$$\begin{gathered} \mathrm{x}°=\frac{360°}{40} \\ =9° \end{gathered}$$                                    بتعويض n=40 في صيغةُ قياسِ الزاويةِ الخارجية للمضلَّعِ المنتظَمِ

11) ذو 45 ضلعًا.

قياس الزاوية الداخلية:

$$\begin{gathered} \mathrm{x}°=\frac{(45-2)\times 180°}{45} \\ =172° \end{gathered}$$                     بتعويض n=45 في صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

قياس الزاوية الخارجية:

$$\begin{gathered} \mathrm{x}°=\frac{360°}{45} \\ =8° \end{gathered}$$                                    بتعويض n=45 في صيغةُ قياسِ الزاويةِ الخارجية للمضلَّعِ المنتظَمِ

12) ذو 60 ضلعًا.

قياس الزاوية الداخلية:

$$\begin{gathered} \mathrm{x}°=\frac{(60-2)\times 180°}{60} \\ =174° \end{gathered}$$                     بتعويض n=60 في صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ المنتظَمِ

قياس الزاوية الخارجية:

$$\begin{gathered} \mathrm{x}°=\frac{360°}{60} \\ =6° \end{gathered}$$                                    بتعويض n=60 في صيغةُ قياسِ الزاويةِ الخارجية للمضلَّعِ المنتظَمِ

 

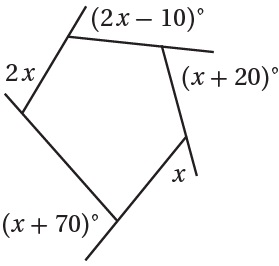
13) أجدُ قيمةَ x في الشّكلِ المُجاورِ: 

$$\begin{gathered} 2\mathrm{x}°+(2\mathrm{x}-10)°+(\mathrm{x}+20)°+\mathrm{x}°+(\mathrm{x}+70)°=360° \\ 7\mathrm{x}+80=360° \\ 7\mathrm{x}=280 \\ \mathrm{x}=40 \end{gathered}$$

 

14) يُمثِّلُ الشّكلُ المُجاورُ مُضَلّعَينِ مُنتظَمينِ مُتجاورَينِ، أَجِدُ $\mathbf{m}\mathbf{\angle }\mathbf{ABC}$

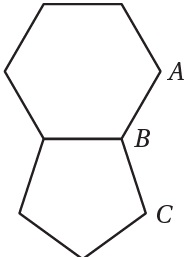
مجموع قياس الزوايا الداخلية للشكلين والزاوية الخارجية ABC هو  = 360°

$\mathrm{m}\angle {\mathrm{x}°}_5+\mathrm{m}\angle {\mathrm{x}°}_6+\mathrm{m}\angle \mathrm{ABC}=360°$

$$\begin{gathered} \mathrm{x}°=\frac{(6-2)\times 180°}{6} \\ =120° \end{gathered}$$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ السداسي المنتظَمِ 

$$\begin{gathered} \mathrm{x}°=\frac{(5-2)\times 180°}{5} \\ =108° \end{gathered}$$                         صيغةُ قياسِ الزاويةِ الداخليةِ للمضلَّعِ الخماسي المنتظَمِ 

$\mathrm{m}\angle \mathrm{ABC}=132°$                              بالتعويض في مجموع قياسات الزوايا 

 

أحدّدُ ما إِذا كانَتِ الجُملةُ الآتِيةُ صَحيحةً دائمًا، أو أحيانًا، أو غَيرَ صَحيحةٍ. أبَرِّرُ إجابتِي.

15) في المُضَلّعاتِ المُنتظمَةِ، يكونُ قياسُ أيٍّ منَ الزّوايا الخارجيّةِ أقَلَّ منْ قِياسِ أيٍّ منَ الزّوايا الدّاخليّةِ.

أحيانا صحيحة ، يعتمد على عدد أضلاع المضلع. تكون صحيحة للخماسي فأكثر وغير صحيحة للمربع والمثلث.

16) في المُضَلّعاتِ المُنتظمَةِ، يكونُ مَجموعُ قِياساتِ الزّوايا الخارجيّةِ يُساوي °360

 صحيحة دائما