رياضيات 5 فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين

أسئة أتحقق من فهمي  

أتحقق من فهمي صفحة 48

أحل كل معادلة مما يأتي ، ثم أتحقق من حلي :

1) y + 4 = 10

2) m - 9 = 11

 

 

الحل : 

2)  m - 9  = 11        20 - 9  = 11      m = 20

1)  y + 4  = 10     6  + 4  = 10      y = 6

 

 

 

 

 

 

---

أتحقق من فهمي صفحة 48

قص عمر 17 cm من شريط فبقي منه 13 cm ، أكتب معادلة لحساب طول الشريط كاملًا ، ثم أحلها.

الحل : 

تكوين المعادلة : 

بالكلمات :  طول الشريط كاملًا  ناقص 17 cm يساوي  13 cm 

بالرموز  :  x  ناقص 17  =  13

المعادلة  : x - 17 = 13 

حل المعادلة  :

$$\begin{gathered} x - 17 = 13 \\ 30 -17 = 13 \\ x = 30 \end{gathered}$$

حل المعادلة x = 30 ، إذن طول الشريط كاملًا  = 30 cm

---

أسئة أتدرب وأحل المسائل 

أحل كل معادلة مما ياتي ، ثم اتحقق من حلي : 

1) x + 4 = 15	2) x - 8  = 18
3) x -  30  = 12	4) b - 19 = 50
5) m + 9 = 100	6) a + 10 = 60

الحل : 

حل المعادلة  x  =  11   التحقق : أعوض عن x بالعدد 11 في المعادلة x  +  4  = 15   $(11 + 4 = 15)$	1) x  +  4  = 15          x  =  15 - 4
حل المعادلة  x  =  26   التحقق : أعوض عن x بالعدد 26 في المعادلة x  $-$  8  = 18  $(26 - 8 = 18)$	2)  x $-$ 8  = 18       x  =  8 + 18
حل المعادلة  x  =  42   التحقق : أعوض عن x بالعدد 42 في المعادلة x $-$ 30 = 12    $(42 - 30 = 12)$	3) x $-$ 30  = 12      x  =  30 + 12
حل المعادلة  b  =  69   التحقق : أعوض عن b بالعدد 69 في المعادلة b $-$19 = 50   $(69 - 19 = 50)$	4) b $-$ 19 = 50       b  = 19 + 50
حل المعادلة  m  =  91   التحقق : أعوض عن m بالعدد 91 في المعادلة m + 9 = 100  $(91 + 9 = 100)$	5) m + 9 = 100       m  =  100 - 9
حل المعادلة  a  =  50   التحقق : أعوض عن a بالعدد 50 في المعادلة  a + 10 = 60    $(50 + 10 = 60)$	6) a + 10 = 60       a  =  60 $-$10

 

7)  أنهار   :  يبلغ طول نهر النيل 6650 km تقريبًا ، ويزيد طوله على طول نهر الأمازون بمقدار    250 km، أكتب معادلة لحساب طول نهر الأمازون ،  

ثم أحلها.

الحل : 

كتابة المعادلة :

بالكلمات : طول نهر الأمازون  +  250 Km  =  طول نهر النيل   

بالرموز  :    x  مضاف إليه 250  = 6650'                      

المعادلة :  x + 250 =  6650  

حل المعادلة : 

$$\begin{gathered} x + 250 = 6650 \\ x = 6650 - 250 \\ x = 6400 \end{gathered}$$

إذن طول نهر الامازون  = $6400 Km$

---

8)  علامات :   مجموع علامات حسن في امتحانين 165 علامةً. إذا كانت علامته في أحد الإمتحانين 80 ؛ أكتب معادلة لحساب علامته في

الإمتحان الآخر ، ثم أحلها.

الحل :  

كتابة المعادلة :

بالكلمات : علامة حسن في امتحان و علامته في امتحان آخر يساوي 165    

بالرموز  :    x  مضافًا إليه 80 = 165                   

المعادلة :  x + 80 =  165  

حل المعادلة :  

$$\begin{gathered} x + 80 = 165 \\ x = 165 - 80 \\ x = 85 \end{gathered}$$

---

9) مياه :  استهلكت منال 45 لترًا من الماء في أثناء ري مزروعاتها، واستهلك مأمون في ري مزروعاته 12 لترًا زيادة عمّا استهلكته منال

  أكتب معادلة لحساب عدد اللترات التي استهلكها مأمون ، ثم أحلها.

الحل :  

كتابة المعادلة :

بالكلمات : استهلاك مأمون للماء ناقص 12 لترًا يساوي استهلاك منال     

بالرموز  :    x  ناقص 12  =  45                     

المعادلة :  x - 12 = 45  

حل المعادلة : 

$$\begin{gathered} x - 12 = 45 \\ x = 12 + 45 \\ x = 57 \end{gathered}$$  

حل المعادلة x = 57  ، إذن استهلاك مأمون للماء  = 57 لتر 

---

أسئة مهارات التفكير العليا 

10) أكتشف الخطأ : حلّ عمار  المعادلة $c - 12 = 15$  فكانت إجابته  c = 3  ، أبين الخطأ الذي وقع فيه ، وأصححه.

الحل :  

الخطأ الذي وقع فيه عمّار  أنه طرح العدد 12 من العدد 15 ، والصحيح هو جمع العدد 12 إلى العدد 15

$$\begin{gathered} c - 12 = 15 \\ c = 12 + 15 \\ c = 27 \end{gathered}$$

---

11) اكتشف المختلف : ما المعادلة المختلفة ؟ أبرر إجابتي .

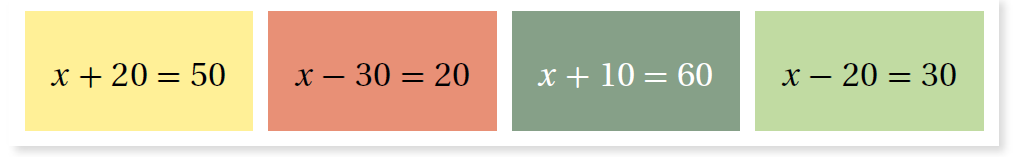
الحل :  

المعادلة المختلفة x + 20 = 50  ، حيث حل المعادلة x =  30  ، بينما حل المعادلات الثلاث الأخرى x = 50 

---

11) تبرير   : إذا كان  $x + 3 = 5$ و  $y + 2 = 5$ ؛ فأبين أنّ $x + 3 = y + 2$   أبرر  إجابتي. 

الحل :  

$$\begin{gathered} x + 3 = 5 \\ x = 5 - 3 \\ x = 2 \end{gathered}$$	$$\begin{gathered} y + 2 = 5 \\ y = 5 - 2 \\ y = 3 \end{gathered}$$
بتعويض x = 2 في المعادلة	بتعويض y = 3 في المعادلة
$2 + 3 = 5$	$3 + 2 = 5$

---

12)   مسألة مفتوحة :  أكتب مسألة تمثلها المعادلة   $b + 25 = 35$ ، ثم أحلها وأجد قيمة b .

الحل :  

اشترت جنى معطف وحقيبة بقيمة 35 دينار  ، إذا كان ثمن المعطف 25 دينار  ، اكتب معادلة لحساب ثمن الحقيبة ثم أحلها .

كتابة المعادلة :

بالكلمات :  ثمنالحقيبة وثمن المعطف يساوي 35 دينار 

بالرموز  :    b  مضافًا إليه 25  = 35                   

المعادلة :   b + 25 = 35  

حل المعادلة :

$$\begin{gathered} b + 25 = 35 \\ b = 35 - 25 \\ b = 10 \end{gathered}$$

حل المعادلة b = 10 ، إذن ثمن الحقيبة 10 دنانير . 

---

 

أسئة كتاب التمارين 

أستخدم النموذج ؛ لأكون معادلة وأحلها في كل مما يأتي :

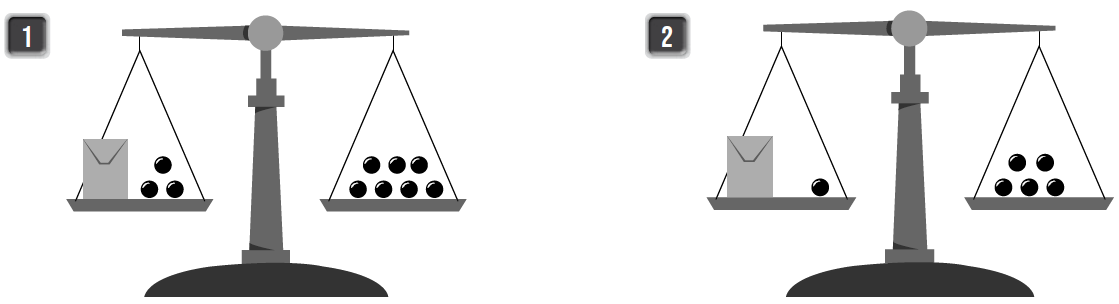
الحل :  

  

$$\begin{gathered} \mathbf{1}\mathbf{)} x + 3 = 7 \\ x = 7 - 3 \\ x = 4 \end{gathered}$$

$$\begin{gathered} \mathbf{2}\mathbf{)}\mathbf{ }x + 1 = 5 \\ x = 5 - 1 \\ x = 4 \end{gathered}$$

---

3) أكمل الجدول الآتي : 

المعادلة	عبارة الجمع أو الطرح التي تحل المعادلة	حل المعادلة	التحقق
n + 7 = 30	n = 30 - 7	n = 23	23 + 7 = 30
$50 + n = 100$	n = 100 - 50	n = 50	$50 + 50 = 100$
y - 5 = 25	y = 5 + 25	y = 30	5 - 30 = 25

---

أحل المعادلات الآتية : 

4) x + 8 = 18	5) 30 + y = 50	6) 14 + m = 44
7) p - 20 = 16	8) y - 50 = 50	9) t - 4 = 3

الحل :  

5) 30 + y = 52     y = 52 - 30     y = 22	4) x + 8 = 18     x = 18 - 8      x  = 10
7) p - 20 = 16     p = 20 + 16     p = 36	6) 14 + m = 44     m = 44 - 14     m = 30
9) t - 4 = 3      t = 4 + 3      t = 7	8) y - 50 = 50     y = 50 + 50     y = 100

---

 

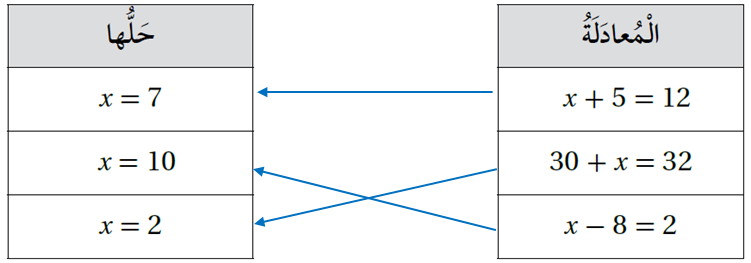
10) أصل بين المعادلة وحلها : 

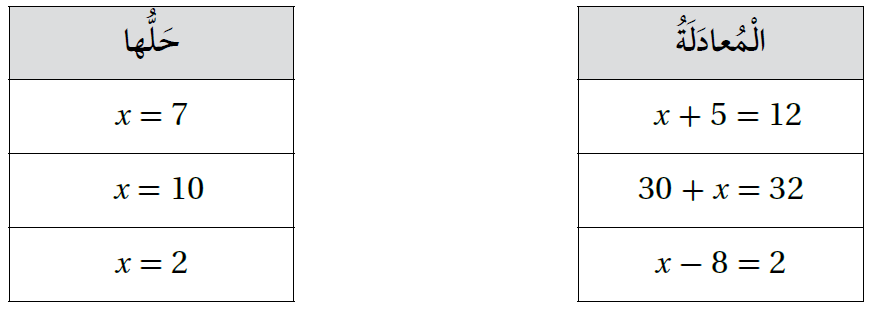
الحل :